Câu hỏi:
78 lượt xemLời giải
Hướng dẫn giải:
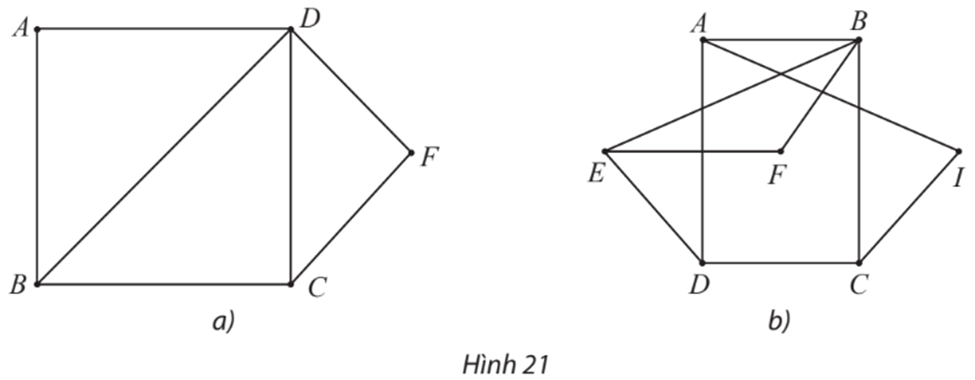
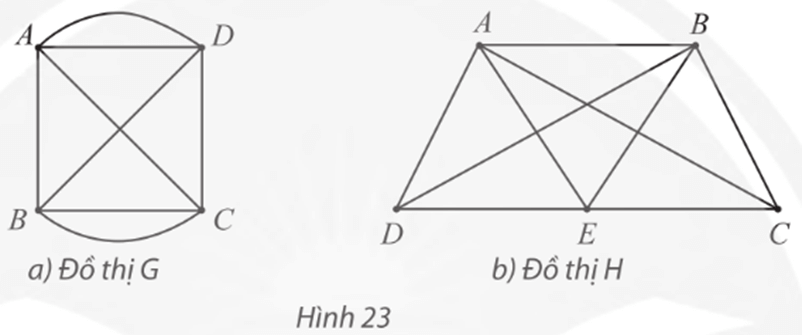
⦁ Hình 21a:
Đồ thị ở Hình 21a có các đỉnh A, F có bậc 2.
Suy ra chu trình Hamilton h (nếu có) phải đi qua các cạnh AB, AD, FD, FC trong đồ thị ở Hình 21a.
Do đó h không thể đi qua các cạnh BD, DC.
Nếu xóa đi hai cạnh này thì đỉnh B, C trở thành có bậc 2.
Vì vậy h phải đi qua cạnh BC.
Khi đó ta được chu trình Hamilton h: ADFCBA.
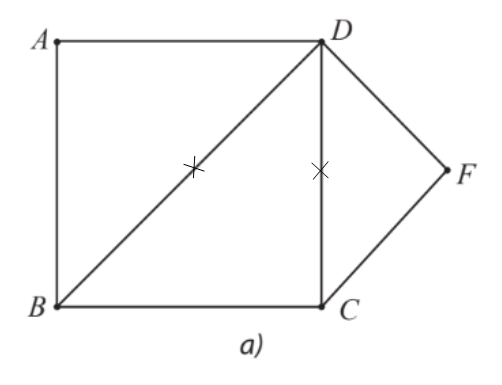
⦁ Hình 21b:
Đồ thị ở Hình 21b có các đỉnh F, I có bậc 2.
Suy ra chu trình Hamilton h (nếu có) phải đi qua các cạnh FE, FB, IA, IC.
Do đó ta được chu trình Hamilton h: AICBFEDA (hoặc AICDEFBA).
Vậy cả hai đồ thị đã cho đều có chu trình Hamilton.
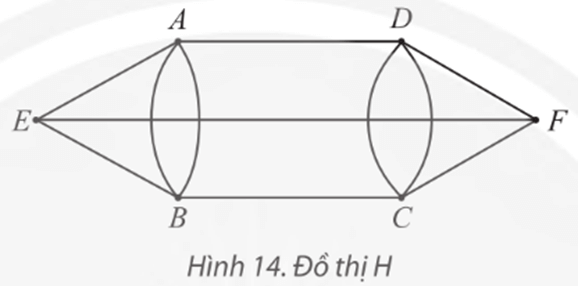
Đồ thị sau có đường đi Euler không? Nếu có, hãy chỉ ra một đường đi như vậy.