Câu hỏi:
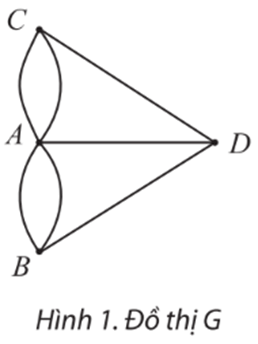
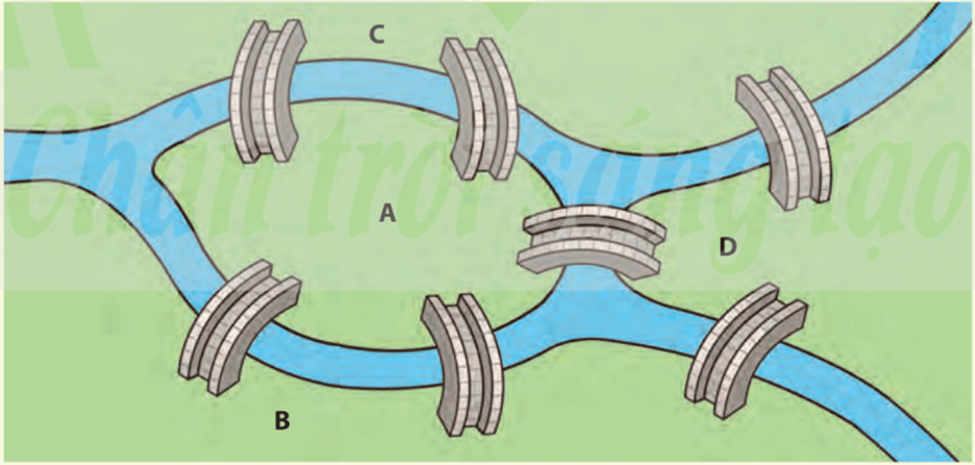
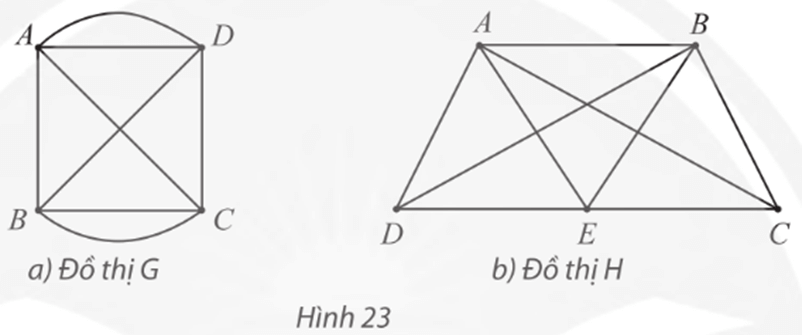
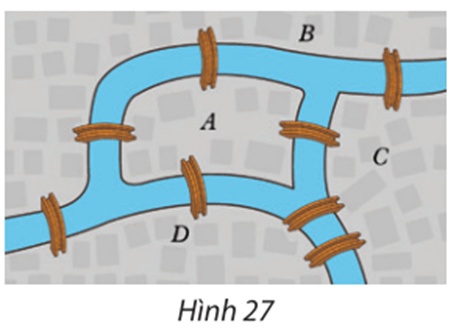
112 lượt xema) Nếu coi mỗi vùng đất của thành phố Königsberg là một đỉnh, mỗi cây cầu là một cạnh nối hai đỉnh thì ta được một đồ thị G như Hình 1.
Câu hỏi của người dân thành phố trở thành: có hay không cách vẽ bằng một nét bút liền (không nhấc bút) đi qua tất cả các cạnh của đồ thị, mỗi cạnh đúng một lần, sao cho điểm kết thúc trùng với điểm xuất phát?
Hãy thử vẽ và đưa ra dự đoán của mình.
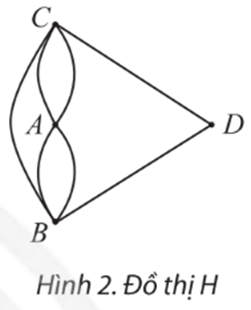
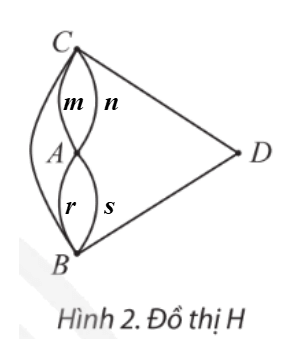
b) Nếu không có cây cầu nối giữa A và D nhưng có thêm một cây cầu nối B và C thì ta có đồ thị H như Hình 2. Có thể vẽ một nét liền đi qua tất cả các cạnh của đồ thị này, mỗi cạnh đúng một lần không?
Lời giải
Hướng dẫn giải:
a) Sau khi thử vẽ, ta dự đoán: không có cách vẽ bằng một nét bút liền (không nhấc bút) đi qua tất cả các cạnh của đồ thị, mỗi cạnh đúng một lần, sao cho điểm kết thúc trùng với điểm xuất phát.
b) Ta có thể vẽ một nét liền đi qua tất cả các cạnh của đồ thị này, mỗi cạnh đúng một lần bằng cách lần lượt vẽ các cạnh m, s, r, n, CB, BD, DC.
Chú ý: Ta có thể bắt đầu vẽ từ đỉnh khác và có thể thay đổi thứ tự các cạnh (đường cong) trong khi vẽ miễn là cách vẽ đó thỏa mãn yêu cầu bài toán.
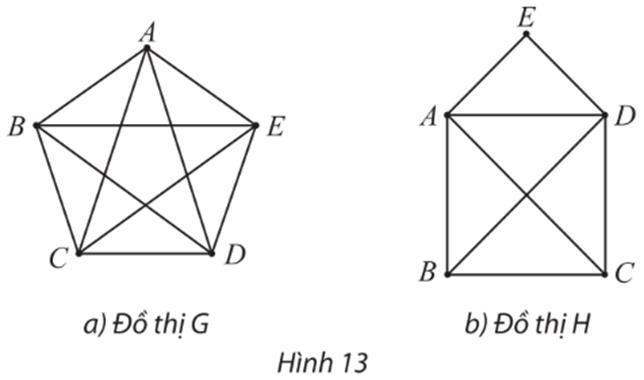
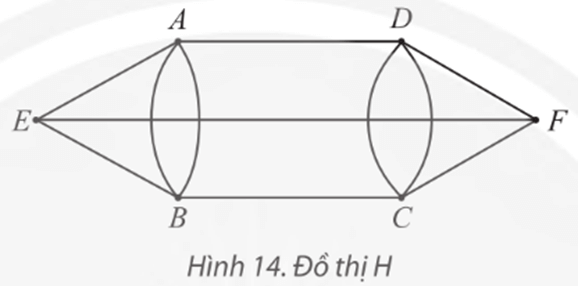
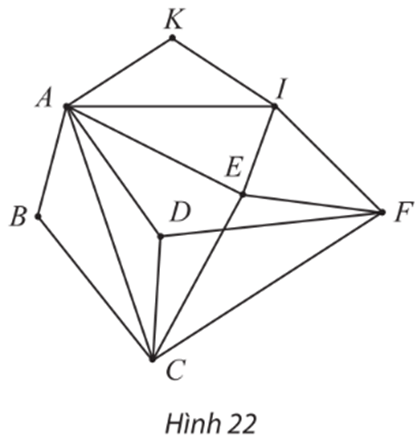
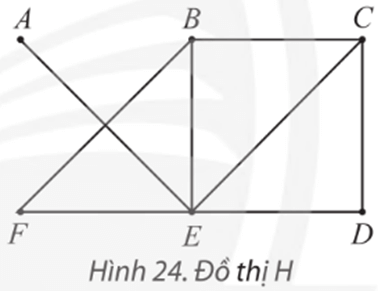
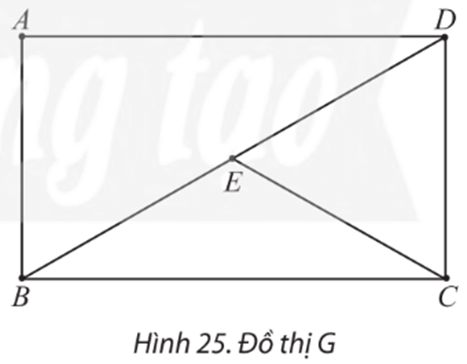
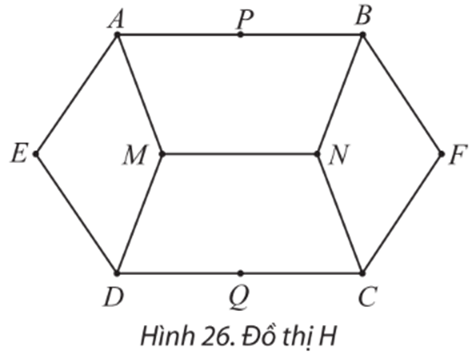
Đồ thị sau có đường đi Euler không? Nếu có, hãy chỉ ra một đường đi như vậy.