Câu hỏi:
80 lượt xem Tự luận
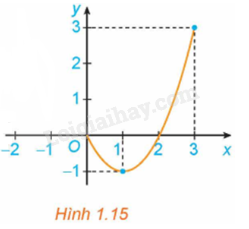
Xét hàm số trên đoạn , với đồ thị như Hình 1.16.
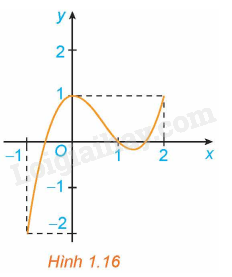
a) Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn .
b) Tính đạo hàm f’(x) và tìm các điểm mà .
c) Tính giá trị của hàm số tại hai đầu mút của đoạn và tại các điểm x đã tìm ở câu b. So sánh số nhỏ nhất trong các giá trị này với , số lớn nhất trong các giá trị này với .
Lời giải
Hướng dẫn giải:
a) Nhìn vào đồ thị ta thấy, trên đoạn ta có:
+ Giá trị lớn nhất của hàm số là .
+ Giá trị nhỏ nhất của hàm số là .
b)
Vậy thì .
c) Ta có:;
Do đó, số nhỏ nhất trong các giá trị này là , số lớn nhất trong các giá trị này là 1.
Ta thấy: , .
Câu 1:
Câu 2:
Câu 4:
Câu 6:
Câu 7:
Câu 8:
Câu 9:
Câu 10: