Câu hỏi:
106 lượt xemCho hàm số .
a) Khảo sát và vẽ đồ thị của hàm số.
b) Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn [2; 4].
Lời giải
Hướng dẫn giải:
a) Xét hàm số .
1. Tập xác định: D = ℝ\{1}.
2. Sự biến thiên:
● Chiều biến thiên:
Đạo hàm y' = . Ta có y' = 0 ⇔ x = – 1 hoặc x = 3.
Trên các khoảng (– ∞; – 1) và (3; + ∞), y' > 0 nên hàm số đồng biến trên mỗi khoảng đó.
Trên các khoảng (– 1; 1) và (1; 3), y' < 0 nên hàm số nghịch biến trên mỗi khoảng đó.
● Cực trị:
Hàm số đạt cực tiểu tại x = 3 và yCT = 10.
Hàm số đạt cực đại tại x = – 1 và yCĐ = 2.
● Các giới hạn tại vô cực và tiệm cận:
Ta có và .
Suy ra đường thẳng y = x + 5 là tiệm cận xiên của đồ thị hàm số.
Ta có . Suy ra đường thẳng x = 1 là tiệm cận đứng của đồ thị hàm số.
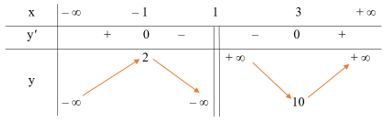
● Bảng biến thiên:
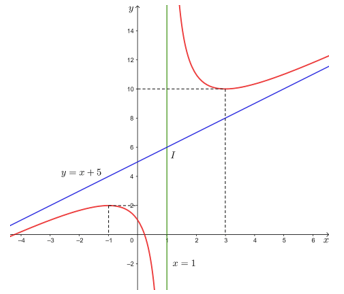
3. Đồ thị:
Ta có y = 0 ⇔ ⇔ x = hoặc x = .
Vậy đồ thị hàm số giao với trục Ox tại điểm và điểm .
Đồ thị hàm số giao với trục Oy tại điểm (0; 1).
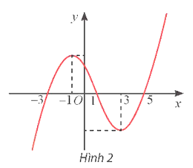
Đồ thị của hàm số đã cho được biểu diễn như hình dưới đây.
Tâm đối xứng của đồ thị hàm số là điểm I(1; 6).
Các trục đối xứng của đồ thị hàm số là hai đường phân giác của các góc tạo bởi hai đường tiệm cận x = 1 và y = x + 5.
b) Xét hàm số với x ∈ [2; 4].
Trên khoảng (2; 4), y' = 0 khi x = 3.
Ta có y(2) = 11; y(3) = 10; y(4) = .
Vậy tại x = 2 và tại x = 3.
Giá trị nhỏ nhất của hàm số trên đoạn [– 2; 3] là
A. .
B. .
C. .
D. 0.
Tiệm cận đứng của đồ thị hàm số là đường thẳng có phương trình
A. .
B. .
C. .
D. .
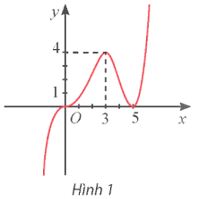
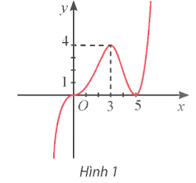
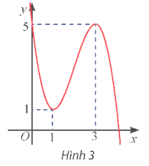
Cho hàm số bậc ba y = f(x) có đồ thị như Hình 3. Viết công thức của hàm số.