Cho hàm số y = f(x) có đồ thị như Hình 1. Hàm số y = f(x) đồng biến trên khoảng

A. (5; + ∞).

B. (3; 5).

C. (0; 5).

D. (3; + ∞).

Cho hàm số y = f(x) có đồ thị như Hình 1.

Hàm số đạt cực đại tại

A. x = 0.

B. x = 3.

C. x = 4.

D. x = 5.

Cho hàm số $y=\frac{x^2-4x+1}{x-4}$. Trong các khẳng định sau, khẳng định nào đúng?

A. Hàm số đạt cực tiểu tại x = 3, giá trị cực tiểu là y = 2.

B. Hàm số đạt cực tiểu tại x = 5, giá trị cực tiểu là y = 6.

C. Hàm số đạt cực tiểu tại x = 3, giá trị cực tiểu là y = 6.

D. Hàm số đạt cực tiểu tại x = 5, giá trị cực tiểu là y = 2.

Đạo hàm của hàm số y = f(x) là hàm số có đồ thị được cho trong Hình 2. Hàm số y = f(x) nghịch biến trên khoảng

A. (– 1; 3).

B. (– 3; 1).

C. (1; 5).

D. (3; + ∞).

Giá trị nhỏ nhất của hàm số $y=\sqrt{x^2+2x+3}$ trên đoạn [– 2; 3] là

A. $\sqrt{3}$.

B. $\sqrt{30}$.

C. $\sqrt{2}$.

D. 0.

Tiệm cận xiên của đồ thị hàm số $y=\frac{2x^3+3x^2-3}{x^2-1}$ là đường thẳng có phương trình

Tiệm cận đứng của đồ thị hàm số $y=\frac{-2x+3}{5x+1}$ là đường thẳng có phương trình

A. $y=-\frac{1}{5}$.

B. $x=-\frac{1}{5}$.

C. $y=-\frac{2}{5}$.

D. $x=-\frac{2}{5}$.

Cho hàm số $y=\frac{-2x-3}{4-x}$. Trong các khẳng định sau, khẳng định nào đúng?

A. Hàm số đồng biến trên (– ∞; – 4) và nghịch biến trên (– 4; + ∞).

B. Hàm số đồng biến trên (– ∞; 4) và (4; + ∞).

C. Hàm số nghịch biến trên (– ∞; 4) và (4; + ∞).

D. Hàm số nghịch biến trên (– ∞; – 4) và (– 4; + ∞).

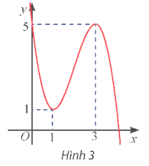
Cho hàm số bậc ba y = f(x) có đồ thị như Hình 3. Viết công thức của hàm số.

Cho hàm số $y=\frac{1}{3}{x}^3-x^2+4$.

a) Khảo sát và vẽ đồ thị của hàm số.

b) Tính khoảng cách giữa hai điểm cực trị của đồ thị hàm số.

Cho hàm số $y=\frac{2x+1}{x-1}$.

a) Khảo sát và vẽ đồ thị của hàm số.

b) Gọi A là giao điểm của đồ thị hàm số với trục Oy, I là giao điểm của hai đường tiệm cận của đồ thị hàm số. Tìm điểm B đối xứng với A qua I. Chứng minh rằng điểm B cũng thuộc đồ thị hàm số này.

Cho hàm số $y=\frac{x^2+4x-1}{x-1}$.

a) Khảo sát và vẽ đồ thị của hàm số.

b) Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn [2; 4].

Cho một hình trụ nội tiếp trong hình nón có chiều cao bằng 12 cm và bán kính đáy bằng 5 cm (Hình 4a). Người ta cắt hình nón, trụ này theo mặt phẳng chứa đường thẳng nối đỉnh và tâm hình tròn đáy của hình nón thì thu được một hình phẳng như Hình 4b.

a) Chứng minh rằng công thức tính bán kính r của đáy hình trụ theo chiều cao h của nó là: $r=\frac{5\left(12-h\right)}{12}$.

b) Chứng minh biểu thức sau biểu thị thể tích khối trụ theo h: $V\left(h\right)=\frac{25\pi h{\left(12-h\right)}^2}{144}$.

c) Tìm h để khối trụ có thể tích lớn nhất.

Trong một nhà hàng, mỗi tuần để chế biến x phần ăn (x lấy giá trị trong khoảng từ 30 đến 120) thì chi phí trung bình (đơn vị: nghìn đồng) của một phần ăn được cho bởi công thức:

$\overline{C}\left(x\right)=2x-230+\frac{7200}{x}$

a) Khảo sát và vẽ đồ thị hàm số $y=\overline{C}\left(x\right)$ trên [30; 120].

b) Từ kết quả trên, tìm số phần ăn sao cho chi phí trung bình của một phần ăn là thấp nhất.

Điện trở R(Ω) của một đoạn dây dẫn hình trụ được làm từ vật liệu có điện trở suất ρ (Ωm), chiều dài ℓ (m) và tiết diện S (m2) được cho bởi công thức

(Vật lí 11 — Chân trời sáng tạo, Nhà xuất bản Giáo dục Việt Nam, 2023, trang 104)

Giả sử người ta khảo sát sự biến thiên của điện trở R theo tiết diện S (ở nhiệt độ 20 °C) của một sợi dây điện dài 10 m làm từ kim loại có điện trở suất ρ và thu được đồ thị hàm số như Hình 6.

a) Có nhận xét gì về sự biến thiên của điện trở R theo tiết điện S?

b) Từ đồ thị, hãy giải thích ý nghĩa của toạ độ giao điểm của đồ thị hàm số với đường thẳng R = 0,001.

c) Tính điện trở suất ρ của dây điện. Từ đó, hãy cho biết dây điện được làm bằng kim loại nào trong số các kim loại được cho ở bảng sau: