Câu hỏi:
126 lượt xem Tự luận
Bài 4.12 trang 58 Toán 10 Tập 1: Cho tứ giác ABCD. Gọi M, N tương ứng là trung điểm của các cạnh AB, CD. Chứng minh rằng
Lời giải
Hướng dẫn giải:
Lời giải
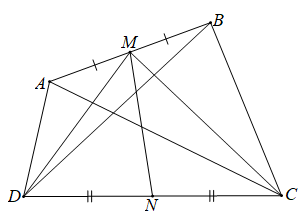
Ta có:
Do đó (1)
Ta có:
Lại có M là trung điểm của AB nên
N là trung điểm của DC, với điểm M bất kì ta có
Suy ra
(2)
Từ (1) và (2) suy ra
Câu 2:
Câu 3:
Câu 4:
Câu 5:
Câu 8:
Câu 9:
Câu 10:
Câu 11:
Câu 13:
Câu 14: