Câu hỏi:
119 lượt xem2. Các tính chất của phép nhân vecto với 1 số
Giải Toán 10 trang 57 Tập 1
HĐ 3 trang 57 Toán 10 Tập 1: Với và hai số thực k, t, những khẳng định nào sau đây là đúng?
a) Hai vectơ và có cùng độ dài bằng
b) Nếu kt ≥ 0 thì cả hai vectơ cùng hướng với .
c) Nếu kt < 0 thì cả hai vectơ ngược hướng với .
d) Hai vectơ và bằng nhau.
Lời giải
Hướng dẫn giải:
Lời giải
a) Ta có: và
Suy ra
Do đó hai vectơ và có cùng độ dài bằng
Vậy khẳng định a) đúng.
b) - Với kt ≥ 0 thì vectơ cùng hướng với vectơ
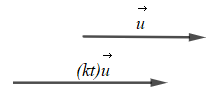
- Với kt ≥ 0 hoặc
+) Trường hợp 1: k ≥ 0 và t ≥ 0
Với t ≥ 0 thì vectơ cùng hướng với vectơ ;
Với k ≥ 0 thì vectơ cùng hướng với vectơ ;
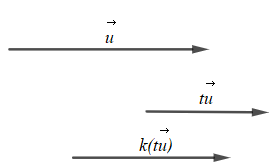
Do đó với k ≥ 0 và t ≥ 0 thì cùng hướng với vectơ (do cùng hướng với ).
+) Trường hợp 2: k ≤ 0 và t ≤ 0
Với t ≤ 0 thì vectơ ngược hướng với vectơ ;
Với k ≤ 0 thì vectơ k() ngược hướng với vectơ ;
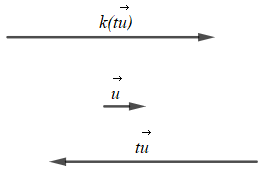
Do đó với k ≤ 0 và t ≤ 0 thì cùng hướng với vectơ (do cùng ngược hướng với
Kết hợp hai trường hợp ta có: với kt ≥ 0 thì cùng hướng với vectơ .
Suy ra: nếu kt ≥ 0 thì cả hai vecto cùng hướng với .
Vậy khẳng định b) là đúng.
c) – Với kt < 0 thì vectơ ngược hướng với vectơ
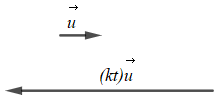
- Với kt < 0 hoặc
+) Trường hợp 1: k > 0 và t < 0
Với t < 0 thì vectơ ngược hướng với vectơ ;
Với k > 0 thì vectơ cùng hướng với vectơ ;
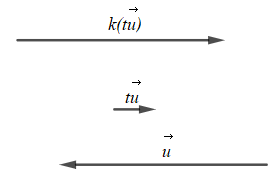
Do đó với k > 0 t < 0 thì ngược hướng với vectơ
+) Trường hợp 2: k < 0 và t > 0
Với t > 0 thì vectơ cùng hướng với vectơ ;
Với k < 0 thì vectơ ngược hướng với vectơ ;
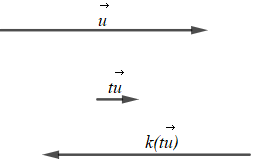
Do đó với k < 0 và t > 0 thì ngược hướng với vectơ .
Kết hợp hai trường hợp ta có: với kt < 0 thì ngược hướng với vectơ .
Suy ra nếu kt < 0 thì cả hai vectơ ngược hướng với .
Vậy khẳng định c) là đúng.
d) Theo câu a thì hai vectơ và có cùng độ dài.
+ Nếu kt ≥ 0 thì cả hai vectơ cùng hướng với .
Suy ra hai vectơ cùng hướng.
+ Nếu kt < 0 thì cả hai vectơ ngược hướng với .
Suy ra hai vectơ cùng hướng.
Do đó hai vectơ cùng hướng với mọi k, t.
Hay hai vectơ và bằng nhau.
Vậy khẳng định d) đúng.