Câu hỏi:
127 lượt xem Tự luận
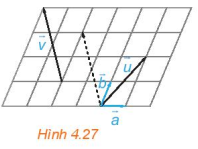
Luyện tập 3 trang 57 Toán 10 Tập 1: Trong Hình 4.27, hãy biểu thị mỗi vectơ theo hai vectơ , tức là tìm các số x, y, z, t để
Lời giải
Hướng dẫn giải:
Lời giải
Giả sử các điểm O, A, B, C, M, N, P là các điểm như trong hình vẽ dưới đây.
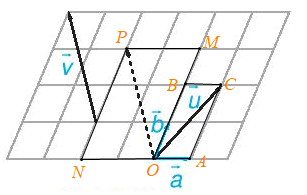
Khi đó ta có:
Xét hình bình hành OACB, có: (quy tắc hình bình hành)
Suy ra .
Xét hình bình hành OMPN, có: (quy tắc hình bình hành)
Suy ra
Vậy
Câu 2:
Câu 3:
Câu 4:
Câu 5:
Câu 8:
Câu 9:
Câu 11:
Câu 12:
Câu 13:
Câu 14: