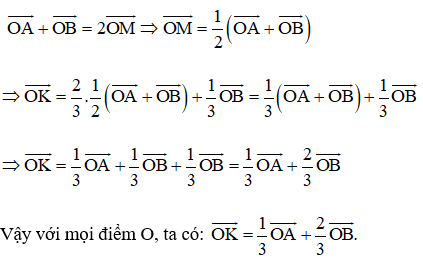Câu hỏi:
110 lượt xemBài 4.13 trang 58 Toán 10 Tập 1: Cho hai điểm phân biệt A và B.
a) Hãy xác định điểm K sao cho
b) Chứng minh rằng với mọi điểm O, ta có:
Lời giải
Hướng dẫn giải:
Lời giải
a) Cách 1:
Giả sử có điểm K thỏa mãn . Khi đó
. Suy ra hai vectơ
và
cùng phương, ngược hướng và KA = 2KB. Suy ra điểm K thuộc đoạn AB và KA = 2KB.

Cách 2:
Gọi M là trung điểm của đoạn thẳng AB suy ra .
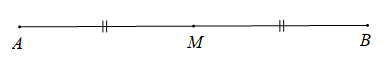
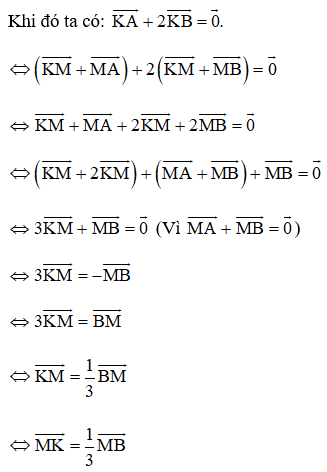
Suy ra vecto cùng hướng với vectơ
và thỏa mãn
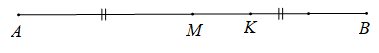
Vậy điểm K là điểm nằm giữa M và B sao cho thỏa mãn
b)
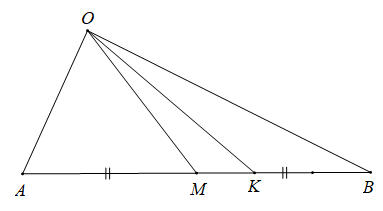
Cách 1:
Ta có:
Mà (theo câu a) do đó
Vậy với mọi điểm O, ta có:
Cách 2:
Ta có:
Theo câu a ta có
Do đó
Vì M là trung điểm của AB nên