Câu hỏi:
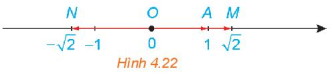
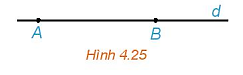
124 lượt xemLuyện tập 1 trang 56 Toán 10 Tập 1: Cho đường thẳng d đi qua hai điểm phân biệt A và B (H.4.25). Những khẳng định nào sau đây là đúng?
a) Điểm M thuộc đường thẳng d khi và chỉ khi tồn tại số t để .
b) Với điểm M bất kì, ta luôn có:
c) Điểm M thuộc tia đối của tia AB khi và chỉ khi tồn tại số t ≤ 0 để
Lời giải
Hướng dẫn giải:
Lời giải
a)
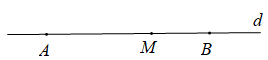
+ Nếu điểm M thuộc đường thẳng d thì ba điểm A, B, M thẳng hàng nên cùng phương
Do đó ta có tồn tại một số thực t thỏa mãn
+ Nếu tồn tại số t thỏa mãn thì cùng phương
Hay đường thẳng AM song song hoặc trùng với đường thẳng AB.
Mà cả hai đường thẳng này đều đi qua A nên đường thẳng AM trùng với đường thẳng AB.
Do đó A, M, B thẳng hàng hay M thuộc đường thẳng d.
Vậy khẳng định a) đúng.
b) Nếu M không thuộc đường thẳng d thì không cùng phương với .
Do đó ta không thể viết dưới dạng
Vậy khẳng định b) sai.
c)
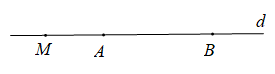
Nếu điểm M thuộc tia đối của tia AB thì hai vectơ và là hai vectơ cùng phương, ngược hướng
Khi đó tồn tại số thực t ≤ 0 thoả mãn
Ngược lại, nếu tồn tại số t ≤ 0 để thì hoặc hai vectơ và ngược hướng (với t < 0) hoặc M ≡ A (với t = 0).
Do đó khẳng định c) đúng.