Câu hỏi:
263 lượt xemTrong 20 phút theo dõi, lưu lượng nước của một con sông được tính theo công thức
Q(t) = ,
trong đó Q được tính theo m3/phút, t tính theo phút, 0 ≤ t ≤ 20 (Nguồn: A. Bigalke et al., Mathematik, Grundkurs ma-1, Cornelsen 2016). Khi lưu lượng nước của con sông lên đến 550 m3/phút thì cảnh báo lũ được đưa ra.
Trong thời gian theo dõi, lưu lượng nước của con sông lớn nhất là bao nhiêu? Cảnh báo lũ được đưa ra vào thời điểm nào?
Lời giải
Hướng dẫn giải:
Xét hàm số Q(t) = với t ∈ [0; 20].
Ta có Q'(t) = ;
Q'(t) = 0 hoặc t = 0.
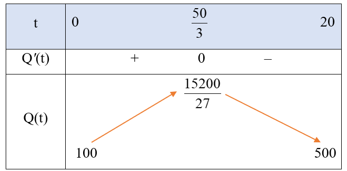
Bảng biến thiên của hàm số trên đoạn [0; 20] như sau:
Từ bảng biến thiên suy ra Q(t) = tại , tức là lưu lượng nước của con sông lớn nhất là m3/phút tại thời điểm phút.
Cảnh báo lũ được đưa ra khi lưu lượng nước của con sông lên đến 550 m3/phút, tức là Q(t) ≥ 550 ⇔ ≥ 550 ⇔ ≥ 0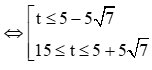
Lại có t ∈ [0; 20] nên .
Vậy tại thời điểm t ∈ [15; 5 +5] phút thì cảnh báo lũ được đưa ra.