Câu hỏi:
83 lượt xemKhảo sát sự biến thiên và vẽ đồ thị của mỗi hàm số sau:
a) y = – x3 + 3x – 2;
b) y = x3 + 3x2 + 3x + 1.
Lời giải
Hướng dẫn giải:
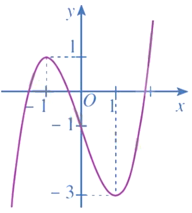
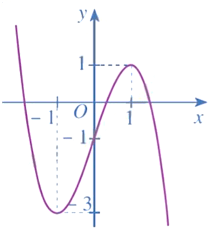
a) y = – x3 + 3x – 2
1) Tập xác định: ℝ.
2) Sự biến thiên:
● Giới hạn tại vô cực: y = - , y = +.
● y' = – 3x2 + 3 = – 3(x2 – 1);
y' = 0 ⇔ – 3(x2 – 1) = 0 ⇔ x = 1 hoặc x = – 1.
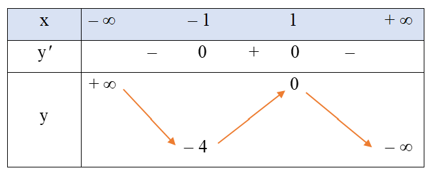
● Bảng biến thiên:
Hàm số đã cho đồng biến trên khoảng (– 1; 1), nghịch biến trên mỗi khoảng (– ∞; – 1) và (1; + ∞).
Hàm số đạt cực đại tại x = 1, yCĐ = 0; hàm số đạt cực tiểu tại x = – 1, yCT = – 4.
3) Đồ thị
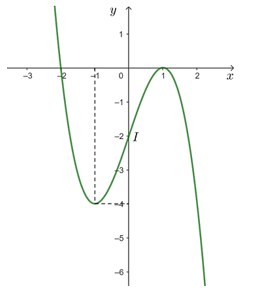
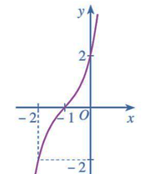
● Giao điểm của đồ thị với trục tung: (0; – 2).
● Giao điểm của đồ thị với trục hoành:
Xét phương trình – x3 + 3x – 2 = 0 ⇔ – (x – 1)2(x + 2) = 0 ⇔ x = 1 hoặc x = – 2.
Vậy đồ thị hàm số giao với trục hoành tại hai điểm (1; 0) và (– 2; 0).
● Đồ thị hàm số đi qua các điểm (– 2; 0), (0; – 2), (1; 0) và (– 1; – 4).
Vậy đồ thị hàm số y = – x3 + 3x – 2 được cho như hình trên.
Tâm đối xứng của đồ thị hàm số đó là điểm I(0; – 2).
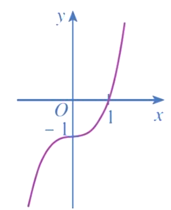
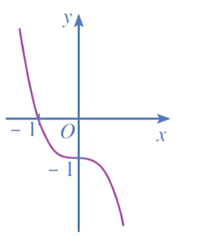
b) y = x3 + 3x2 + 3x + 1
1) Tập xác định: ℝ.
2) Sự biến thiên:
● Giới hạn tại vô cực: y = +, = - .
● y' = 3x2 + 6x + 3 = 3(x + 1)2;
y' ≥ 0 với mọi x ∈ ℝ;
y' = 0 khi x = – 1.
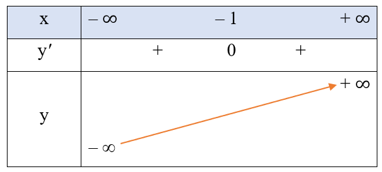
● Bảng biến thiên:
Hàm số đồng biến trên khoảng (– ∞; + ∞).
Hàm số không có cực trị.
3) Đồ thị
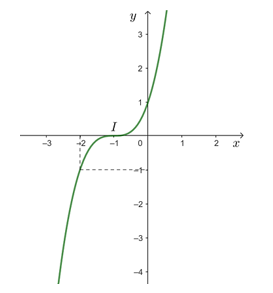
● Giao điểm của đồ thị với trục tung: (0; 1).
● Giao điểm của đồ thị với trục hoành:
Giải phương trình x3 + 3x2 + 3x + 1 = 0 ta được x = – 1.
Vậy đồ thị hàm số giao với trục hoành tại điểm (– 1; 0).
● Đồ thị hàm số đi qua các điểm (– 1; 0), (0; 1), (– 2; – 1).
Vậy đồ thị hàm số y = x3 + 3x2 + 3x + 1 được cho như hình vẽ trên.
Tâm đối xứng của đồ thị hàm số đó là điểm I(– 1; 0).