Câu hỏi:
112 lượt xem Tự luận
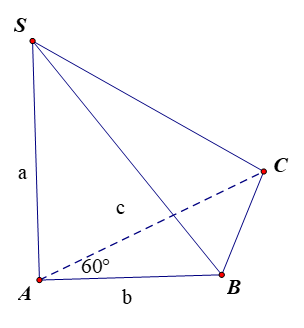
Cho hình chóp S.ABC có SA (ABC) và , biết diện tích các tam giác ABC, SAB và SAC lần lượt là 3; 9; 12. Tính thể tích khối chóp S.ABC.
Lời giải
Hướng dẫn giải:
Đặt SA = a, AB = b, AC = c.
Khi đó .
Theo đề bài, .
Do SA (ABC) nên SA AB hay tam giác SAB vuông tại A.
Khi đó .
Do SA (ABC) nên SA AC hay tam giác SAC vuông tại A.
Khi đó .
Do đó (abc)2 = 12 × 18 × 24 = 722, suy ra abc = 72.
Vậy .
Câu 1:
Câu 2:
Câu 3:
Câu 4:
Câu 5:
Câu 6:
Câu 8: