Câu hỏi:
110 lượt xem Tự luận
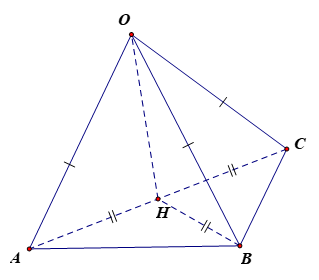
Cho tứ diện OABC có OA = OB = OC = a và ; ; . Tính theo a thể tích khối tứ diện OABC.
Lời giải
Hướng dẫn giải:
Xét tam giác OAB vuông tại O, có AB = .
Xét tam giác BOC có OB = OC và nên tam giác BOC là tam giác đều.
Do đó BC = a.
Áp dụng định lí Côsin trong tam giác OAC có:
-2.OA.OC.cos
= a2+a2+2.a2. = 3a2
Có . Do đó AC2 = AB2 + BC2.
Vì AC2 = AB2 + BC2 nên tam giác ABC vuông tại B.
Do đó .
Kẻ OH (ABC) tại H.
Vì OA = OB = OC nên HA = HB = HC.
Khi đó, H là trung điểm của AC nên AH = .
Xét tam giác OAH vuông tại H, có OH = .
Vậy .
Câu 1:
Câu 2:
Câu 3:
Câu 5:
Câu 6:
Câu 7:
Câu 8: