Câu hỏi:
182 lượt xem Tự luận
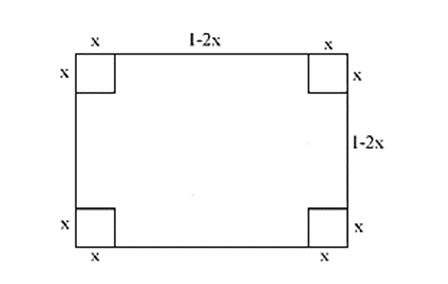
Người ta cắt bỏ bốn hình vuông cùng kích thước ở bốn góc của một tấm tôn hình vuông có cạnh 1 m để gò lại thành một chiếc thùng có dạng hình hộp chữ nhật không nắp. Hỏi cạnh của các hình vuông cần bỏ đi có độ dài bằng bao nhiêu để thùng hình hộp nhận được có thể tích lớn nhất.
Lời giải
Hướng dẫn giải:
Gọi x (m) là độ dài cạnh hình vuông nhỏ tại mỗi góc của tấm tôn được cắt bỏ đi (với 0<x<). Thể tích hình hộp chữ nhật nhận được là:
V = (1-2x)2.x = .(1-2x).(1-2x).4x. = .
Dấu “=” xảy ra khi 1 – 2x = 4x x = .
Vậy để thể tích chiếc thùng là lớn nhất thì các cạnh của hình vuông được cắt bỏ đi là m.
Câu 1:
Câu 2:
Câu 3:
Câu 4:
Câu 5:
Câu 6: