Câu hỏi:

100 lượt xem

Cho hình vẽ biết AB∥MxAB\parallel Mx, MNMN và NPNP vuông góc với nhau, ABM^=BMN^=135∘.\widehat {ABM} = \widehat {BMN} = 135^\circ .

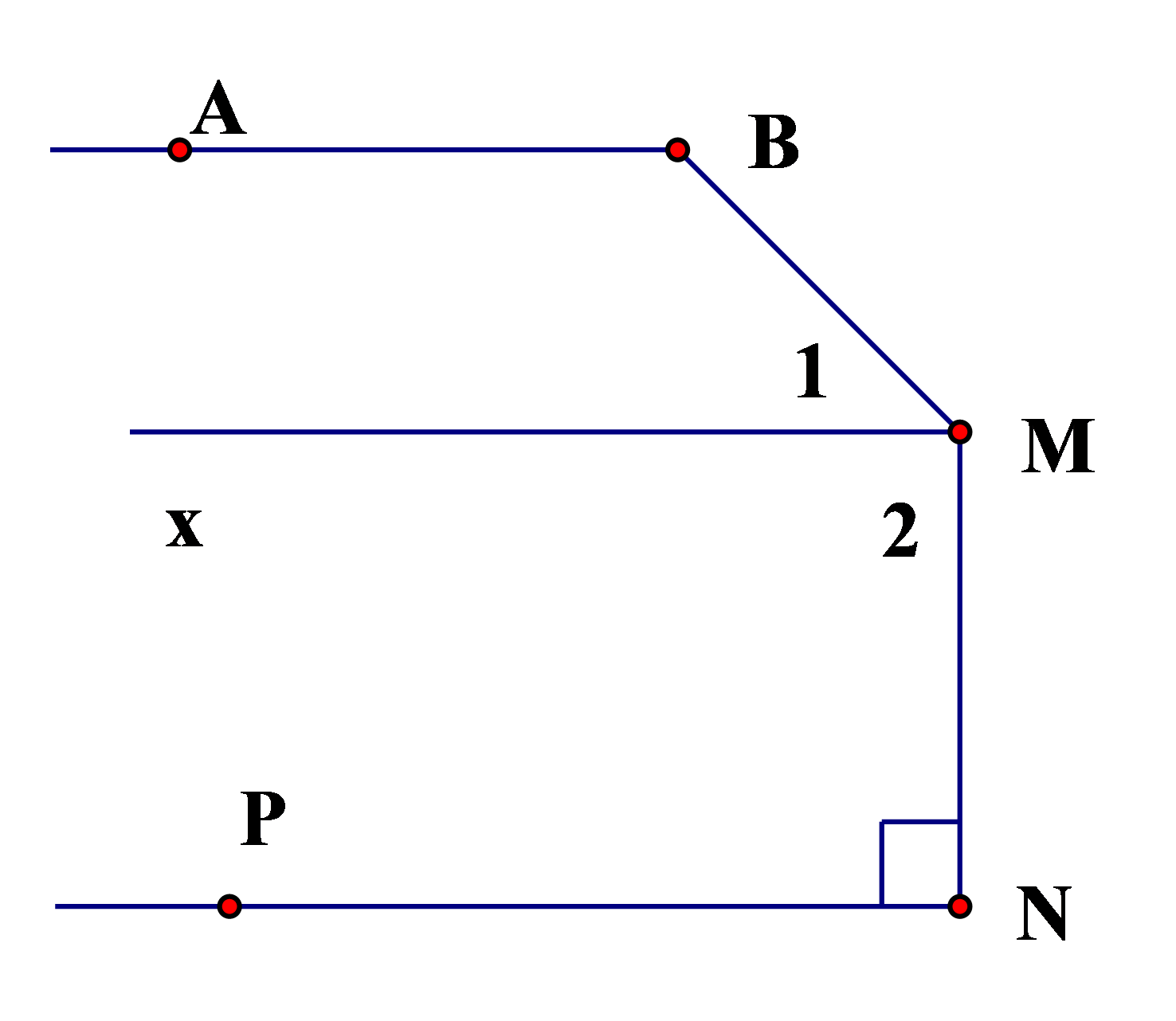
loading...

1) Tính số đo các góc M1^,  M2^\widehat {{M_1}},\,\,\widehat {{M_2}}.

2) Chứng minh: AB∥NPAB\parallel NP.

        3) Kẻ tia phân giác của MNP^\widehat {MNP}, cắt tia MxMx tại điểm QQ. Chứng minh: NQ∥MBNQ\parallel MB.

Hướng dẫn giải:

GT, KL: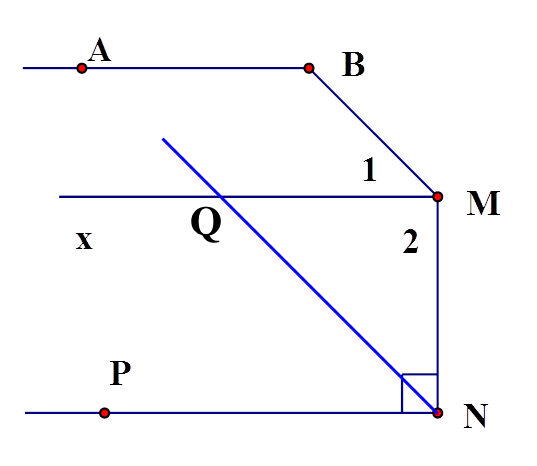loading...

Để làm ý 1,2 HS không cần thiết phải vẽ hình

1) Ta có: AB∥MxAB\parallel Mx ÞABM^+M1^=180∘\widehat {ABM} + \widehat {{M_1}} = 180^\circ

Hay 135∘ +M1^=180∘135^\circ  + \widehat {{M_1}} = 180^\circ ÞM1^=180∘ −135∘ =45∘\widehat {{M_1}} = 180^\circ  - 135^\circ  = 45^\circ

    Vì BMN^=135∘\widehat {BMN} = 135^\circ ÞM1^+M2^=180∘\widehat {{M_1}} + \widehat {{M_2}} = 180^\circ ÞM2^=135∘ −45∘ =90∘\widehat {{M_2}} = 135^\circ  - 45^\circ  = 90^\circ

2) Vì M2^=90∘\widehat {{M_2}} = 90^\circ Þ Mx⊥MNMx \bot MN

   Mà NP⊥MNNP \bot MN (gt)

   Nên Mx∥NPMx\parallel NP  (vì cùng vuông góc với MNMN)

   Do đó AB∥NPAB\parallel NP (vì cùng song song với MxMx).

3) Vì MQ là tia phân giác của MNP^\widehat {MNP}

ÞMNQ^=QNP^=12MNP^\widehat {MNQ} = \widehat {QNP} = \frac{1}{2}\widehat {MNP} ÞMNQ^=QNP^=12 . 90∘ =45∘\widehat {MNQ} = \widehat {QNP} = \frac{1}{2}\,.\,90^\circ  = 45^\circ

Vì Mx∥NPMx\parallel NP ÞNQM^=QNP^=45∘\widehat {NQM} = \widehat {QNP} = 45^\circ (cặp góc so le trong)

ÞNQM^=M1^(=45∘)\widehat {NQM} = \widehat {{M_1}}( = 45^\circ ) Þ NQ∥MBNQ\parallel MB (đpcm)

Xem đáp án

Xem thêm: Đề thi học kì 1 Toán 7 KNTT có đáp án - Đề 2

Lời giải

Hướng dẫn giải:

​

GT, KL:loading...

Để làm ý 1,2 HS không cần thiết phải vẽ hình

1) Ta có: \[AB\parallel Mx\] Þ\(\widehat {ABM} + \widehat {{M_1}} = 180^\circ \)

Hay \(135^\circ  + \widehat {{M_1}} = 180^\circ \)Þ\(\widehat {{M_1}} = 180^\circ  - 135^\circ  = 45^\circ \)

    Vì \(\widehat {BMN} = 135^\circ \)Þ\(\widehat {{M_1}} + \widehat {{M_2}} = 180^\circ \)Þ\(\widehat {{M_2}} = 135^\circ  - 45^\circ  = 90^\circ \)

2) Vì \(\widehat {{M_2}} = 90^\circ \)Þ \(Mx \bot MN\)

   Mà \(NP \bot MN\) (gt)

   Nên \[Mx\parallel NP\]  (vì cùng vuông góc với \[MN\])

   Do đó \[AB\parallel NP\] (vì cùng song song với \[Mx\]).

3) Vì MQ là tia phân giác của \(\widehat {MNP}\)

Þ\(\widehat {MNQ} = \widehat {QNP} = \frac{1}{2}\widehat {MNP}\) Þ\[\widehat {MNQ} = \widehat {QNP} = \frac{1}{2}\,.\,90^\circ  = 45^\circ \]

Vì \[Mx\parallel NP\] Þ\(\widehat {NQM} = \widehat {QNP} = 45^\circ \) (cặp góc so le trong)

Þ\(\widehat {NQM} = \widehat {{M_1}}( = 45^\circ )\) Þ \[NQ\parallel MB\] (đpcm)

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

Trong các khẳng định dưới đây, khẳng định đúng là:

52∈Q\frac{5}{2} \in \mathbb{Q}.
7,5∈Z7,5 \in \mathbb{Z}.
95∈N\frac{9}{5} \in \mathbb{N}.
−32∉Q\frac{{ - 3}}{2} \notin \mathbb{Q}.
1 năm trước 42 lượt xem
Câu 2:

Trong các số dưới đây, số vô tỉ là

14.\sqrt {\frac{1}{4}} .
2,1422,142.
3.\sqrt 3 .
0.
1 năm trước 40 lượt xem
Câu 3:

Khi x =6\sqrt {\rm{x}}  = 6 thì xx có giá trị là

12.
−12 - 12.
36.
−36 - 36.
1 năm trước 37 lượt xem
Câu 4:

Khi ∣x∣=25\left| x \right| = 25 thì xx có giá trị là

x=25x = 25.
x  =−−25x\; = --25.
x∈{5;  −5}x \in \left\{ {5;\,\, - 5} \right\}.
x∈{25;  −25}x \in \left\{ {25;\,\, - 25} \right\}.
1 năm trước 36 lượt xem
Câu 5:

Cho biết a=5 = 2,2360679...a = \sqrt 5 \, = \,2,2360679..., khi làm tròn số a với độ chính xác 0,05 ta được:

2,22,2.
2,242,24.
2,232,23.
2,2362,236.
1 năm trước 50 lượt xem
Câu 6:

Số đường thẳng đi qua điểm MM nằm ngoài đường thẳng aa và song song với đường thẳng a là

1.
2.
0.
vô số.
1 năm trước 44 lượt xem
Câu 7:

Cho hình vẽ bên, biết AB∥CDAB\parallel CD thì góc bằng ABD^\widehat {ABD} là

BAD^.\widehat {BAD}.
BCD^.\widehat {BCD}.
ADB^.\widehat {ADB}.
BDC^.\widehat {BDC}.
1 năm trước 67 lượt xem
Câu 8:

Cho hình vẽ, biết CxCx là tia phân giác của ACy^\widehat {ACy} thì ACx^\widehat {ACx} có số đo là

50∘.50^\circ .
60∘.60^\circ .
65∘.65^\circ .
80∘.80^\circ .
1 năm trước 45 lượt xem
Câu 9:

Thực hiện phép tính (tính hợp lý nếu có thể) :

1) 34+123−79\frac{3}{4} + 1\frac{2}{3} - \frac{7}{9};                                2) 17⋅(43)2−17:911\frac{1}{7} \cdot {\left( {\frac{4}{3}} \right)^2} - \frac{1}{7}:\frac{9}{{11}};

3) (−49+35):115+(15−59):115\left( { - \frac{4}{9} + \frac{3}{5}} \right):1\frac{1}{5} + \left( {\frac{1}{5} - \frac{5}{9}} \right):1\frac{1}{5};               4) 0,5.49+(13−1,5)2−(23)9:(23)70,5.\frac{4}{9} + {\left( {\frac{1}{3} - 1,5} \right)^2} - {\left( {\frac{2}{3}} \right)^9}:{\left( {\frac{2}{3}} \right)^7}.

Hướng dẫn giải:

1) 34+123−79= 34+53−79=2736+6036−2836=5936\frac{3}{4} + 1\frac{2}{3} - \frac{7}{9} = \,\frac{3}{4} + \frac{5}{3} - \frac{7}{9} = \frac{{27}}{{36}} + \frac{{60}}{{36}} - \frac{{28}}{{36}} = \frac{{59}}{{36}}

2) 17⋅(43)2−17:911\frac{1}{7} \cdot {\left( {\frac{4}{3}} \right)^2} - \frac{1}{7}:\frac{9}{{11}}=17⋅169−17⋅119 = \frac{1}{7} \cdot \frac{{16}}{9} - \frac{1}{7} \cdot \frac{{11}}{9}

=17(169−119)=17⋅59=563 = \frac{1}{7}\left( {\frac{{16}}{9} - \frac{{11}}{9}} \right) = \frac{1}{7} \cdot \frac{5}{9} = \frac{5}{{63}}

3) (−49+35):115+(15−59):115\left( { - \frac{4}{9} + \frac{3}{5}} \right):1\frac{1}{5} + \left( {\frac{1}{5} - \frac{5}{9}} \right):1\frac{1}{5}

=(−49+35):65+(15−59):65 = \left( { - \frac{4}{9} + \frac{3}{5}} \right):\frac{6}{5} + \left( {\frac{1}{5} - \frac{5}{9}} \right):\frac{6}{5}

=(−49+35).56+(15−59).56 = \left( { - \frac{4}{9} + \frac{3}{5}} \right).\frac{5}{6} + \left( {\frac{1}{5} - \frac{5}{9}} \right).\frac{5}{6}

=(−49+35+15−59).56 = \left( { - \frac{4}{9} + \frac{3}{5} + \frac{1}{5} - \frac{5}{9}} \right).\frac{5}{6}= −15.56= −16 =  - \frac{1}{5}.\frac{5}{6} =  - \frac{1}{6}.

4)  0,5.49+(13−1,5)2−(23)9:(23)7\,0,5.\frac{4}{9} + {\left( {\frac{1}{3} - 1,5} \right)^2} - {\left( {\frac{2}{3}} \right)^9}:{\left( {\frac{2}{3}} \right)^7}

=12.49+(13−32)2−(23)2 = \frac{1}{2}.\frac{4}{9} + {\left( {\frac{1}{3} - \frac{3}{2}} \right)^2} - {\left( {\frac{2}{3}} \right)^2}=29+(−76)2−49 = \frac{2}{9} + {\left( {\frac{{ - 7}}{6}} \right)^2} - \frac{4}{9}

=29+4936−49=4136 = \frac{2}{9} + \frac{{49}}{{36}} - \frac{4}{9} = \frac{{41}}{{36}}.
1 năm trước 35 lượt xem
Câu 10:

Tìm xx, biết:

1) 52x−34=14\frac{5}{2}x - \frac{3}{4} = \frac{1}{4}                                                           

2) x+420=5x+4\,\frac{{x + 4}}{{20}} = \frac{5}{{x + 4}}

Hướng dẫn giải:

1) 52x−34=14⇔  52x=14+34\frac{5}{2}x - \frac{3}{4} = \frac{1}{4} \Leftrightarrow \,\,\frac{5}{2}x = \frac{1}{4} + \frac{3}{4}

⇔ 52x=1⇔ x=1:52⇔ x=25 \Leftrightarrow \,\frac{5}{2}x = 1 \Leftrightarrow \,x = 1:\frac{5}{2} \Leftrightarrow \,x = \frac{2}{5}

2) x+420=5x+4⇔  (x+4)(x+4)=5 . 20\frac{{x + 4}}{{20}} = \frac{5}{{x + 4}} \Leftrightarrow \,\,(x + 4)(x + 4) = 5\,.\,20

⇔ (x+4)2=100 \Leftrightarrow \,{(x + 4)^2} = 100

 ⇔  [x+4=10x+4= −10⇔  [x=6x= −14\, \Leftrightarrow \,\,\left[ \begin{array}{l}x + 4 = 10\\x + 4 =  - 10\end{array} \right. \Leftrightarrow \,\,\left[ \begin{array}{l}x = 6\\x =  - 14\end{array} \right.

Vậy x∈{6;  −14}x \in \left\{ {6;\,\, - 14} \right\}.
1 năm trước 42 lượt xem
Câu 11:

Tùng, Huy và Minh cùng trồng hoa cúc trong chậu để bán dịp tết. Tùng trồng được 6 chậu hoa, Huy trồng được 4 chậu hoa và Minh trồng được 5 chậu hoa. Ba bạn bán hết hoa thu được tổng số tiền là 1,5 triệu đồng. Ba bạn quyết định chia tiền tỉ lệ với số chậu hoa trồng được. Tính số tiền mỗi bạn nhận được?

Hướng dẫn giải:

Gọi số tiền ba bạn Tùng, Huy và Minh nhận được lần lượt là x,y,zx,{\rm{ }}y,{\rm{ }}z (x,y,z>0)\left( {x,{\rm{ }}y,{\rm{ }}z > 0} \right) (triệu đồng)

Vì tổng số tiền ba bạn nhận được khi bán hết chậu hoa là 1,51,5 triệu đồng nên ta có: x+y+z=1,5x + y + z = 1,5.

Vì số tiền mỗi bạn nhận được tỉ lệ với số chậu hoa trồng được nên ta có: x6=y4=z5\frac{x}{6} = \frac{y}{4} = \frac{z}{5}.

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

x6=y4=z5=x+y+z6+4+5=1,515=0,1\frac{x}{6} = \frac{y}{4} = \frac{z}{5} = \frac{{x + y + z}}{{6 + 4 + 5}} = \frac{{1,5}}{{15}} = 0,1

Suy ra:x6=0,1⇒x=0,1.6=0,6\frac{x}{6} = 0,1 \Rightarrow x = 0,1.6 = 0,6

   y4=0,1⇒y=0,1.4=0,4\frac{y}{4} = 0,1 \Rightarrow y = 0,1.4 = 0,4         

   z5=0,1⇒y=0,1.5=0,5\frac{z}{5} = 0,1 \Rightarrow y = 0,1.5 = 0,5 (thỏa mãn)               

Vậy số tiền bạn Tùng, Huy và Minh nhận được lần lượt là: 0,6 triệu đồng, 0,4 triệu đồng, 0,5 triệu đồng.
1 năm trước 50 lượt xem
Câu 13:

Tìm x,y,zx,{\rm{ }}y,{\rm{ }}z biết:

3x−2y4=2z−4x3=4y−3z2\frac{{3x - 2y}}{4} = \frac{{2z - 4x}}{3} = \frac{{4y - 3z}}{2} và x+y−−z= −10x + y--z =  - 10.

Hướng dẫn giải:

Ta có:3x−2y4=2z−4x3=4y−3z2\frac{{3x - 2y}}{4} = \frac{{2z - 4x}}{3} = \frac{{4y - 3z}}{2}

⇒12x−8y16=6z−12x9=8y−6z4 \Rightarrow \frac{{12x - 8y}}{{16}} = \frac{{6z - 12x}}{9} = \frac{{8y - 6z}}{4}

=12x−8y+6z−12x+8y−6z14+9+4=0 = \frac{{12x - 8y + 6z - 12x + 8y - 6z}}{{14 + 9 + 4}} = 0

Do đó:

{3x−2y=02z−4x=04y−3z=0⇒{3x=2y2z=4x4y=3z⇒{x2=y 3    (1)z4=x2y3=z4    (2)\left\{ \begin{array}{l}3x - 2y = 0\\2z - 4x = 0\\4y - 3z = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}3x = 2y\\2z = 4x\\4y = 3z\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\frac{x}{2} = \frac{{y\,}}{3}\,\,\,\,(1)\\\frac{z}{4} = \frac{x}{2}\\\frac{y}{3} = \frac{z}{4}\,\,\,\,(2)\end{array} \right.

Từ (1) và (2) ta có: x2=y 3=z4\frac{x}{2} = \frac{{y\,}}{3} = \frac{z}{4}

Suy ra : x2=y 3=z4=x+y−z2+3−4=−101= −10\frac{x}{2} = \frac{{y\,}}{3} = \frac{z}{4} = \frac{{x + y - z}}{{2 + 3 - 4}} = \frac{{ - 10}}{1} =  - 10

Từ đó ta có: x= −20;y= −30;z= −40x =  - 20;{\rm{ }}y =  - 30;{\rm{ }}z =  - 40.
1 năm trước 44 lượt xem

ĐỀ THI LIÊN QUAN: