Câu hỏi:
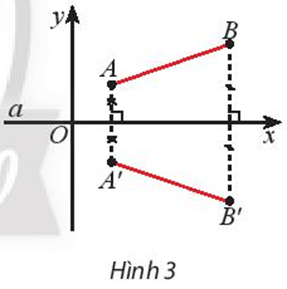
96 lượt xemGiả sử Đa là phép đối xứng trục qua đường thẳng a. Ta chọn hệ tọa độ Oxy sao cho trục Ox trùng với a. Lấy hai điểm tùy ý A(xA; yA) và B(xB; yB). Gọi A’, B’ lần lượt là ảnh của A, B qua phép đối xứng trục a (Hình 3). Xác định tọa độ của A’ và B’ rồi dùng công thức tính khoảng cách để so sánh A’B’ và AB.
Lời giải
Hướng dẫn giải:
⦁ Ta có A’ là ảnh của A qua Đa.
Suy ra a là đường trung trực của đoạn thẳng AA’ hay Ox là đường trung trực của đoạn thẳng AA’.
Do đó A’ đối xứng với A qua Ox nên chúng có cùng hoành độ và có tung độ đối nhau.
Vì vậy tọa độ A’(xA; –yA).
Tương tự như vậy, ta được tọa độ B’(xB; –yB).
Vậy tọa độ A’(xA; –yA) và B’(xB; –yB).
⦁ Ta có .
Suy ra .
Ta lại có .
Suy ra:
.
Vậy A’B’ = AB.
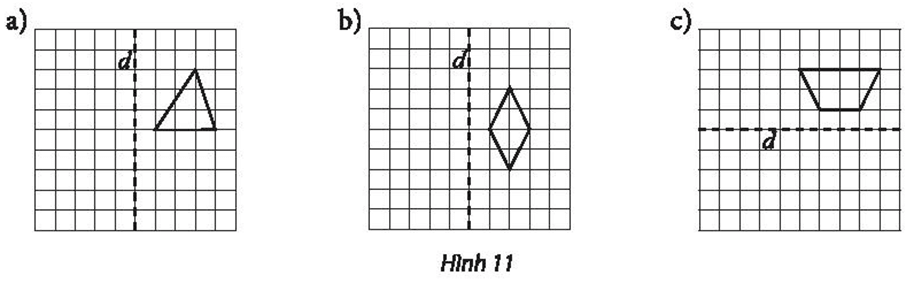
Tìm trục đối xứng của một hình thang cân ABCD có hai đáy là AB và CD.