Câu hỏi:
90 lượt xemLời giải
Hướng dẫn giải:
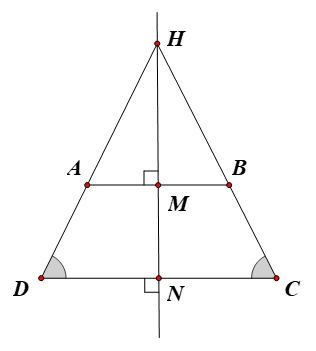
Gọi H là giao điểm của AD và BC.
Ta có (do ABCD là hình thang cân).
Suy ra tam giác HCD cân tại H.
Do đó HD = HC.
Vì vậy HD – AD = HC – BC (AD = BC vì ABCD là hình thang cân có hai đáy AB, CD).
Suy ra HA = HB.
Do đó tam giác HAB cân tại H.
Gọi M, N lần lượt là trung điểm của AB và CD.
Tam giác HCD cân tại H có HN là đường trung tuyến.
Suy ra HN cũng là đường cao của tam giác HCD, do đó HN ⊥ CD.
Chứng minh tương tự, ta được HM ⊥ AB.
Mà AB // CD (chứng minh trên).
Suy ra HM ⊥ CD
Lại có HN ⊥ CD (chứng minh trên).
Do đó ba điểm H, M, N thẳng hàng.
Ta có M là trung điểm AB và MN ⊥ AB (chứng minh trên).
Suy ra MN là đường trung trực của hai đoạn thẳng AB.
Khi đó B = ĐMN(A) và A = ĐMN(B).
Chứng minh tương tự, ta được D = ĐMN(C) và C = ĐMN(D).
Do đó ảnh của hình thang cân ABCD qua ĐMN là chính nó.
Vậy trục đối xứng cần tìm là đường thẳng MN, với M, N lần lượt là trung điểm của AB và CD.