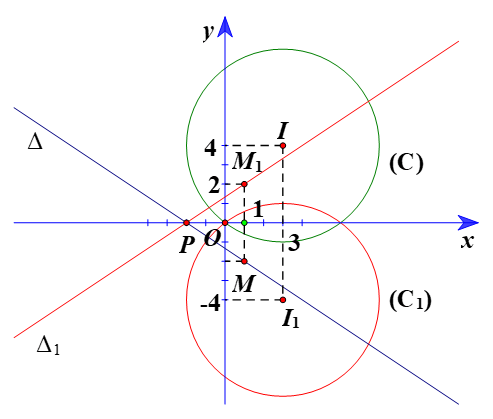
Đường tròn (C) có tâm I(3; 4), bán kính R = 5.

a)

⦁ Gọi (C₁) là ảnh của (C) qua Đ_Ox, khi đó (C₁) có tâm I₁ là ảnh của I(3; 4) Đ_Ox và bán kính R₁ = R = 5.

Ta có I₁ = Đ_Ox(I).

Suy ra Ox là đường trung trực của đoạn II₁

Do đó hai điểm I(3; 4) và I₁ có cùng hoành độ và có tung độ đối nhau.

Vì vậy tọa độ I₁(3; –4).

Vậy ảnh của đường tròn (C) qua Đ_Ox là đường tròn (C₁) có phương trình là:

(x – 3)² + (y + 4)² = 25.

⦁ Trục Ox: y = 0.

Với y = 0, ta có 2x + 3.0 + 4 = 0 ⇔ x = –2.

Suy ra giao điểm của ∆ và trục Ox là điểm P(–2; 0).

Khi đó P = Đ_Ox(P).

Chọn M(1; –2) ∈ ∆.

Gọi M₁ và ∆₁ theo thứ tự là ảnh của M và ∆ qua Đ_Ox.

Ta thấy Ox là đường trung trực của đoạn MM₁.

Do đó hai điểm M(1; –2) và M₁ có cùng hoành độ và có tung độ đối nhau.

Vì vậy tọa độ M₁(1; 2).

Ta có $\overrightarrow{M_{1}P}=\left(-3;-2\right)$.

Đường thẳng ∆₁ có vectơ chỉ phương $\overrightarrow{M_{1}P}=\left(-3;-2\right)$.

Suy ra ∆₁ có vectơ pháp tuyến ${\overrightarrow{n}}_{{\Delta }_1}=\left(2;-3\right)$.

Vậy đường thẳng ∆₁ đi qua P(–2; 0) và có vectơ pháp tuyến ${\overrightarrow{n}}_{{\Delta }_1}=\left(2;-3\right)$ nên có phương trình là:

2(x + 2) – 3(y – 0) = 0 hay 2x – 3y + 4 = 0.

b)

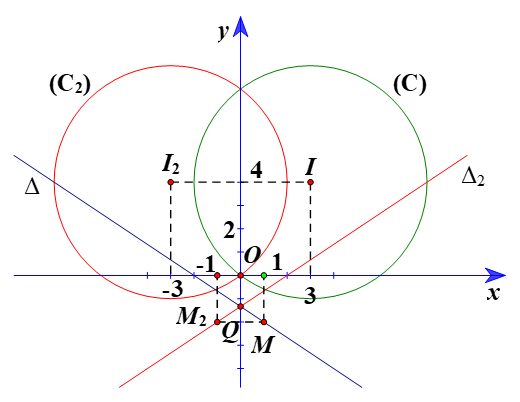
⦁ Gọi (C₂) là ảnh của (C) qua Đ_Oy, khi đó (C₂) có tâm I₂ là ảnh của I(3; 4) qua Đ_Oy và bán kính R₂ = R = 5.

Ta có I₂ = Đ_Oy(I).

Suy ra Oy là đường trung trực của đoạn II₂.

Do đó hai điểm I(3; 4) và I₂ có cùng tung độ và có hoành độ đối nhau.

Vì vậy tọa độ I₂(–3; 4).

Vậy ảnh của đường tròn (C) qua Đ_Oy là đường tròn (C₂) có phương trình là:

(x + 3)² + (y – 4)² = 25.

⦁ Trục Oy: x = 0.

Với x = 0, ta có 2.0 + 3y + 4 = 0 ⇔ $y=-\frac{4}{3}$.

Suy ra giao điểm của ∆ và trục Oy là điểm $Q\left(0;-\frac{4}{3}\right)$.

Khi đó Q = Đ_Oy(Q).

Chọn M(1; –2) ∈ ∆.

Gọi M₂ và ∆₂ theo thứ tự là ảnh của M và ∆ qua Đ_Oy.

Ta thấy Oy là đường trung trực của đoạn MM₂.

Do đó hai điểm M(1; –2) và M₂ có cùng tung độ và có hoành độ đối nhau.

Vì vậy tọa độ M₂(–1; –2).

Ta có $\overrightarrow{M_{2}Q}=\left(1;\frac{2}{3}\right)$.

Đường thẳng ∆₂ có vectơ chỉ phương ${\overrightarrow{u}}_2=3\overrightarrow{M_{2}Q}=\left(3;2\right)$.

Suy ra ∆₂ có vectơ pháp tuyến ${\overrightarrow{n}}_{{\Delta }_2}=\left(2;-3\right)$.

Vậy đường thẳng ∆₂ đi qua M₂(–1; –2) và có vectơ pháp tuyến ${\overrightarrow{n}}_{{\Delta }_2}=\left(2;-3\right)$ nên có phương trình là:

2(x + 1) – 3(y + 2) = 0 hay 2x – 3y – 4 = 0.

c)

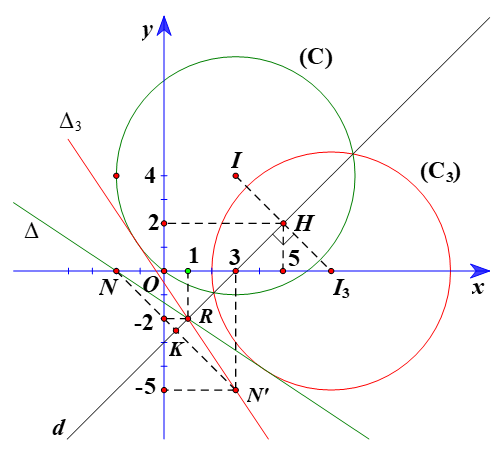
⦁ Gọi (C₃) là ảnh của (C) qua Đ_d, khi đó (C₂) có tâm I₃ là ảnh của I(3; 4) qua Đ_d và bán kính R₃ = R = 5.

Ta có I₃ = Đ_d(I).

Suy ra d là đường trung trực của đoạn II₃ nên II₃ ⊥ d tại trung điểm của II₃.

Mà đường thẳng d: x – y – 3 = 0 có vectơ pháp tuyến ${\overrightarrow{n}}_d=\left(1;-1\right)$.

Suy ra đường thẳng II₃ có vectơ chỉ phương ${\overrightarrow{n}}_d=\left(1;-1\right)$.

Do đó đường thẳng II₃ có vectơ pháp tuyến $\overrightarrow{u}=\left(1;1\right)$.

Vì vậy đường thẳng II₃ đi qua điểm I(3; 4) và nhận $\overrightarrow{u}=\left(1;1\right)$ làm vectơ pháp tuyến nên có phương trình là:

1(x – 3) + 1(y – 4) = 0 ⇔ x + y – 7 = 0.

Gọi H là giao điểm của II₃ và đường thẳng d.

Suy ra tọa độ H thỏa mãn hệ phương trình $\left\{\begin{array}{l}\mathrm{x}-\mathrm{y}-3=0\\ \mathrm{x}+\mathrm{y}-7=0\end{array}\right.\iff \left\{\begin{array}{l}\mathrm{x}=5\\ \mathrm{y}=2\end{array}\right.$

Do đó tọa độ H(5; 2).

Ta có H là trung điểm II₃.

Suy ra $\left\{\begin{array}{l}{\mathrm{x}}_{{\mathrm{I}}_3}=2{\mathrm{x}}_{\mathrm{H}}-{\mathrm{x}}_{\mathrm{I}}=2.5-3=7\\ {\mathrm{y}}_{{\mathrm{I}}_3}=2{\mathrm{y}}_{\mathrm{H}}-{\mathrm{y}}_{\mathrm{I}}=2.2-4=0\end{array}\right.$

Do đó tọa độ I₃(7; 0).

Vậy ảnh của đường tròn (C) qua Đ_d là đường tròn (C₃) có phương trình là:

(x – 7)² + y² = 25.

⦁ Gọi R là giao điểm của ∆ và d.

Suy ra tọa độ R thỏa mãn hệ phương trình:

$\left\{\begin{array}{l}2\mathrm{x}+3\mathrm{y}+4=0\\ \mathrm{x}-\mathrm{y}-3=0\end{array}\right.\iff \left\{\begin{array}{l}\mathrm{x}=1\\ \mathrm{y}=-2\end{array}\right.$

Do đó tọa độ R(1; –2).

Khi đó R = Đ_d(R).

Chọn N(–2; 0) ∈ ∆: 2x + 3y + 4 = 0.

Gọi N’ và ∆₃ theo thứ tự là ảnh của N và ∆ qua Đ_d.

Ta thấy d là đường trung trực của đoạn NN’.

Mà đường thẳng d: x – y – 3 = 0 có vectơ pháp tuyến ${\overrightarrow{n}}_d=\left(1;-1\right)$.

Suy ra đường thẳng NN’ có vectơ chỉ phương ${\overrightarrow{n}}_d=\left(1;-1\right)$.

Do đó đường thẳng NN’ có vectơ pháp tuyến $\overrightarrow{u}=\left(1;1\right)$.

Vì vậy đường thẳng NN’ đi qua N(–2; 0) và nhận $\overrightarrow{u}=\left(1;1\right)$ làm vectơ pháp tuyến nên có phương trình là:

1(x + 2) + 1(y – 0) = 0 ⇔ x + y + 2 = 0.

Gọi K là giao điểm của NN’ và đường thẳng d.

Suy ra tọa độ K thỏa mãn hệ phương trình:

$\left\{\begin{array}{l}\mathrm{x}+\mathrm{y}+2=0\\ \mathrm{x}-\mathrm{y}-3=0\end{array}\right.\iff \left\{\begin{array}{l}\mathrm{x}=\frac{1}{2}\\ \mathrm{y}=-\frac{5}{2}\end{array}\right.$

Do đó tọa độ $K\left(\frac{1}{2};-\frac{5}{2}\right)$.

Ta có K là trung điểm NN’.

Suy ra $\left\{\begin{array}{l}{\mathrm{x}}_{{\mathrm{N}}^{\text{'}}}=2{\mathrm{x}}_{\mathrm{K}}-{\mathrm{x}}_{\mathrm{N}}=2.\frac{1}{2}+2=3\\ {\mathrm{y}}_{{\mathrm{N}}^{\text{'}}}=2{\mathrm{y}}_{\mathrm{K}}-{\mathrm{y}}_{\mathrm{N}}=2.\left(-\frac{5}{2}\right)-0=-5\end{array}\right.$

Do đó tọa độ N’(3; –5).

Với R(1; –2), ta có $\overrightarrow{N^{\text{'}}R}=\left(-2;3\right)$.

Đường thẳng ∆₃ có vectơ chỉ phương $\overrightarrow{N^{\text{'}}R}=\left(-2;3\right)$.

Suy ra ∆₃ có vectơ pháp tuyến ${\overrightarrow{n}}_{{\Delta }_3}=\left(3;2\right)$.

Vậy đường thẳng ∆₃ đi qua N’(3; –5) và nhận ${\overrightarrow{n}}_{{\Delta }_3}=\left(3;2\right)$ làm vectơ pháp tuyến nên có phương trình là:

3(x – 3) + 2(y + 5) = 0 hay 3x + 2y + 1 = 0.