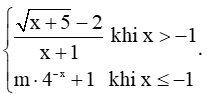Câu hỏi:
129 lượt xemGiả sử un là số hạng thứ n của dãy số (un) và .
a) Chứng tỏ rằng u1 = 1, u2 = 1 và un + 2 = un + 1 + un với mọi n ℕ*. Từ đó suy ra (un) là dãy số Fibonacci.
b) Viết 11 số hạng đầu tiên của dãy Fibonacci và 10 tỉ số đầu tiên.
Tính .
Lời giải
Hướng dẫn giải:
a) Ta có an + 2 – bn + 2 = an + 1.a − bn + 1.b
= an + 1.a + an + 1.b − bn + 1.b − bn + 1.a − an + 1.b + bn + 1.a
= an + 1.(a + b) − bn + 1.(a + b) – ab(an − bn)
= (an + 1 − bn + 1).(a + b) – ab(an − bn) (*)
Có .
.
Áp dụng (*), ta có:
= un+1 + un.
Vậy un + 2 = un+1 + un. Do đó (un) là dãy Fibonacci.
b) Ta có bảng sau
|
n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
un |
1 |
1 |
2 |
3 |
5 |
8 |
13 |
21 |
34 |
55 |
89 |
|
1 |
2 |
Ta có
Hàm số y = cos là hàm số tuần hoàn với chu kì
A. 2π.
B. π.
C. .
D. 3π.
Giá trị của m để hàm số 
A. 3.
B. 1.
C. −3.
D. −1.
Cho mẫu số liệu ghép nhóm sau về thời gian sử dụng mạng xã hội của một nhóm học sinh trong ngày.
|
Thời gian (giờ) |
[0; 0,5) |
[0,5; 1) |
[1; 1,5) |
[1,5; 2) |
[2; 2,5) |
|
Số học sinh |
2 |
5 |
8 |
6 |
4 |
Thời gian (giờ) sử dụng mạng xã hội trung bình trong ngày của nhóm học sinh là
A. 1,0.
B. 1,25.
C. 1,35.
D. 1,5.
Cho mẫu số liệu ghép nhóm sau về thời gian sử dụng mạng xã hội của một nhóm học sinh trong ngày.
|
Thời gian (giờ) |
[0; 0,5) |
[0,5; 1) |
[1; 1,5) |
[1,5; 2) |
[2; 2,5) |
|
Số học sinh |
2 |
5 |
8 |
6 |
4 |
Nhóm chứa tứ phân vị thứ ba là nhóm
A. [0,5; 1).
B. [1; 1,5).
C. [1,5; 2).
D. [2; 2,5).
Giải các phương trình sau:
a) ;
b) log3(x2 – x – 3) = log3(2x – 1) + 1.
Cho các hàm số f(x) = 32x −1 và g(x) = xln9. Giải bất phương trình f'(x) < g'(x).
Một công ty bất động sản đã thống kê số lượng khách hàng theo giá đất họ đầu tư và thu được kết quả như sau:
|
Mức giá (triệu đồng/m2) |
[10; 15) |
[15; 20) |
[20; 25) |
[25; 30) |
[30; 35) |
|
Số khách hàng |
15 |
25 |
38 |
29 |
13 |
a) Ước lượng mức giá có nhiều khách hàng lựa chọn nhất.
b) Công ty muốn hướng đến 25% khách hàng cao cấp nhất thì nên kinh doanh bất động sản với mức giá ít nhất là bao nhiêu?
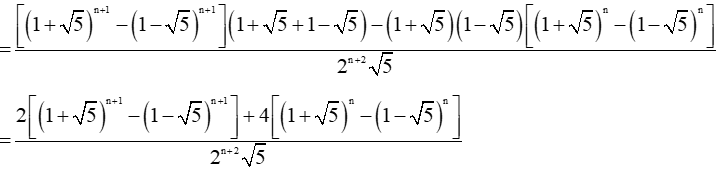
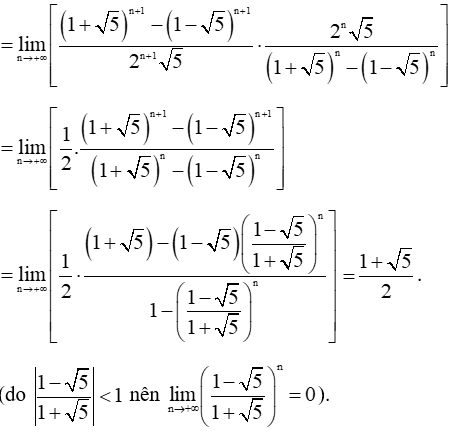
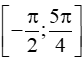 là
là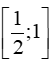 .
.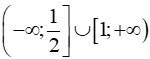 .
.