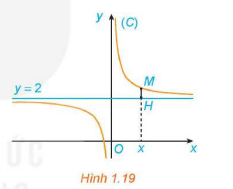
Cho hàm số có đồ thị (C). Với , xét điểm M (x; f(x)) thuộc (C). Gọi H là hình chiếu vuông góc của M trên đường thẳng (H.1.22).
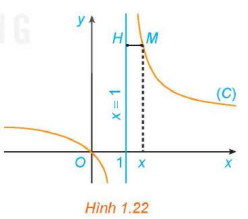
a) Tính khoảng cách MH.
b) Khi M thay đổi trên (C) sao cho khoảng cách MH dần đến 0, có nhận xét gì về tung độ của điểm M?
Giải Toán 12 (Kết nối tri thức) Bài 3: Đường tiệm cận của đồ thị hàm số
Một nhà sản xuất cần làm ra những chiếc bình có dạng hình trụ với dung tích . Mặt trên và mặt dưới của bình được làm bằng vật liệu có giá 1,2 nghìn đồng/, trong khi mặt bên của bình được làm bằng vật liệu có giá 0,75 nghìn đồng/. Tìm các kích thước của bình để chi phí vật liệu sản xuất mỗi chiếc bình là nhỏ nhất.
Giải Toán 12 (Kết nối tri thức) Bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
Một nhà sản xuất muốn thiết kế một chiếc hộp có dạng hình hộp chữ nhật không có nắp, có đáy là hình vuông và diện tích bề mặt bằng như Hình 1.17. Tìm các kích thước của chiếc hộp sao cho thể tích của hộp là lớn nhất.
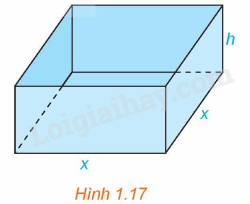
Giải Toán 12 (Kết nối tri thức) Bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
Giả sử sự lây lan của một loại virus ở một địa phương có thể được mô hình hóa bằng hàm số trong đó N là số người bị nhiễm bệnh (tính bằng trăm người) và t là thời gian (tuần).
a) Hãy ước tính số người tối đa bị nhiễm bệnh ở địa phương đó.
b) Đạo hàm N’(t) biểu thị tốc độ lây lan của virus (còn gọi là tốc độ truyền bệnh). Hỏi virus sẽ lây lan nhanh nhất khi nào?
Giải Toán 12 (Kết nối tri thức) Bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
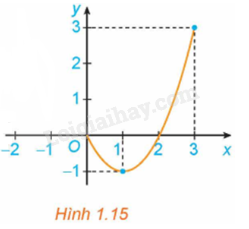
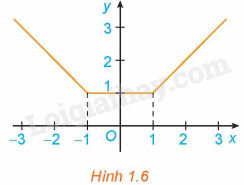
Xét hàm số trên đoạn , với đồ thị như Hình 1.16.
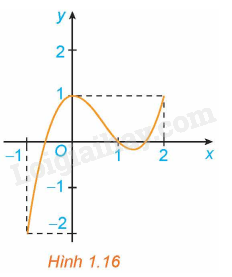
a) Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn .
b) Tính đạo hàm f’(x) và tìm các điểm mà .
c) Tính giá trị của hàm số tại hai đầu mút của đoạn và tại các điểm x đã tìm ở câu b. So sánh số nhỏ nhất trong các giá trị này với , số lớn nhất trong các giá trị này với .
Giải Toán 12 (Kết nối tri thức) Bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
Giả sử doanh số (tính bằng số sản phẩm) của một sản phẩm mới (trong vòng một số năm nhất định) tuân theo quy luật logistic được mô hình hóa bằng hàm số trong đó thời gian t được tính bằng năm, kể từ khi phát hành sản phẩm mới. Khi đó, đạo hàm f’(t) sẽ biểu thị tốc độ bán hàng. Hỏi sau khi phát hành bao nhiêu năm thì tốc độ bán hàng là lớn nhất?
Giải Toán 12 (Kết nối tri thức) Bài 1: Tính đơn điệu và cực trị của hàm số
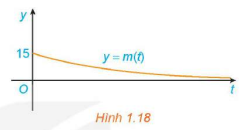
Giả sử số dân của một thị trấn sau t năm kể từ năm 2000 được mô tả bởi hàm số , trong đó N(t) được tính bằng nghìn người.
a) Tính số dân của thị trấn đó vào các năm 2000 và 2015.
b) Tính đạo hàm N’(t) và . Từ đó giải thích tại sao dân số của thị trấn đó luôn tăng nhưng sẽ không vượt qua một ngưỡng nào đó.
Giải Toán 12 (Kết nối tri thức) Bài 1: Tính đơn điệu và cực trị của hàm số
Tìm các khoảng đồng biến, khoảng nghịch biến của các hàm số có đồ thị như sau:
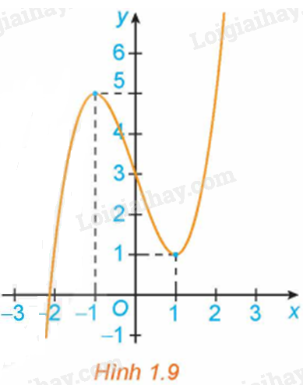
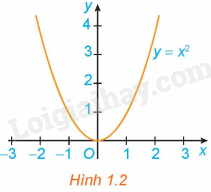
a) Đồ thị hàm số (H.1.11);
Tìm các khoảng đồng biến, khoảng nghịch biến của các hàm số có đồ thị như sau:
a) Đồ thị hàm số (H.1.11);
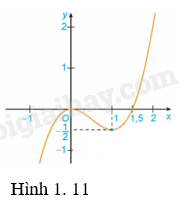
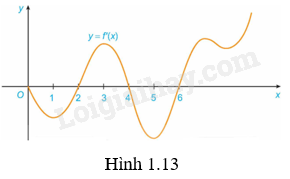
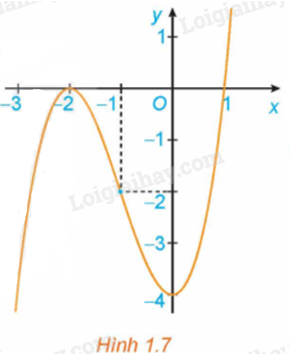
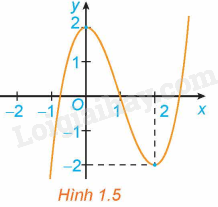
b) Đồ thị hàm số (H.1.12).
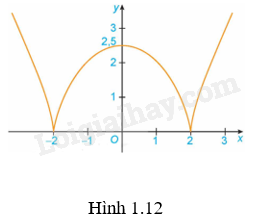
Giải Toán 12 (Kết nối tri thức) Bài 1: Tính đơn điệu và cực trị của hàm số
Một vật được phóng thẳng đứng lên trên từ độ cao 2m với vận tốc ban đầu là 24,5m/s. Trong Vật lí, ta biết rằng khi bỏ qua sức cản của không khí thì độ cao h (mét) của vật sau t (giây) được cho bởi công thức: . Hỏi tại thời điểm nào thì vật đạt độ cao lớn nhất?
Giải Toán 12 (Kết nối tri thức) Bài 1: Tính đơn điệu và cực trị của hàm số
Giải bài toán trong tình huống mở đầu bằng cách thực hiện lần lượt các yêu cầu sau:
a) Theo ý nghĩa cơ học của đạo hàm, vận tốc v(t) là đạo hàm của s(t). Hãy tìm vận tốc v(t).
b) Xét dấu của hàm v(t), từ đó suy ra câu trả lời.
Bài toán mở đầu:
Xét một chất điểm chuyển động trên một trục số nằm ngang, chiều dương từ trái sang phải (H.1.1). Giả sử vị trí s(t) (mét) của chất điểm trên trục số đã chọn tại thời điểm t (giây) được cho bởi công thức . Hỏi trong khoảng thời gian nào thì chất điểm chuyển động sang phải, trong khoảng thời gian nào thì chất điểm chuyển động sang trái?

Giải Toán 12 (Kết nối tri thức) Bài 1: Tính đơn điệu và cực trị của hàm số
Cho hàm số .
a) Tính đạo hàm và tìm các điểm x mà .
b) Lập bảng biến thiên của hàm số, tức là lập bảng thể hiện dấu của đạo hàm và sự đồng biến, nghịch biến của hàm số trên các khoảng tương ứng.
c) Nếu kết luận về khoảng đồng biến, nghịch biến của hàm số.
Giải Toán 12 (Kết nối tri thức) Bài 1: Tính đơn điệu và cực trị của hàm số