Câu hỏi:
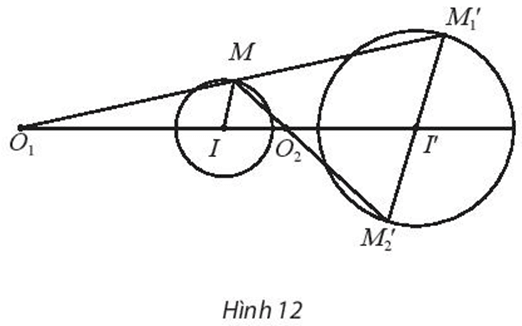
88 lượt xemCho hai đường tròn (I; R) và (I’; R’) (Hình 12) có tâm phân biệt và bán kính khác nhau. Hãy chứng minh có hai phép vị tự biến đường tròn (I; R) thành đường tròn (I’; R’).
Lời giải
Hướng dẫn giải:
Lấy điểm M bất kì thuộc (I; R).
Đường thẳng qua I’ và song song với IM cắt đường tròn (I’; R’) tại hai điểm và (giả sử M, nằm cùng phía đối với đường thẳng II’ và M, nằm khác phía đối với đường thẳng II’).
Giả sử đường thẳng cắt đường thẳng II’ tại điểm O1 nằm ngoài đoạn OO’ và đường thẳng cắt đường thẳng II’ tại điểm O2 nằm trong đoạn II’.
Ta có biến đường tròn (I; R) thành đường tròn (I’; R’).
Suy ra R’ = |k|.R.
Do đó .
Mà k > 0 (do I, I’ nằm cùng phía đối với O1).
Suy ra .
Ta có biến đường tròn (I; R) thành đường tròn (I’; R’).
Chứng minh tương tự, ta được khi I, I’ nằm khác phía đối với O2, ta có .
Vậy ta có hai phép vị tự thỏa mãn yêu cầu bài toán là và .
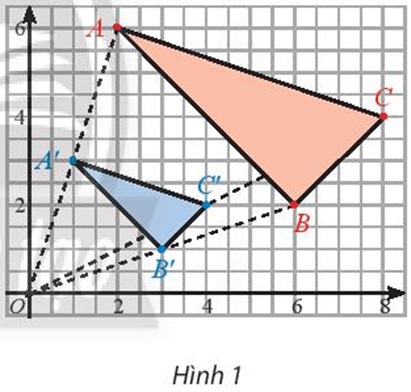
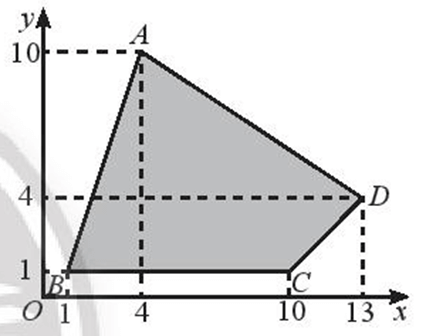
Vẽ Hình 11 ra giấy kẻ ô li và tìm ảnh của tứ giác ABCD qua phép vị tự .