Câu hỏi:
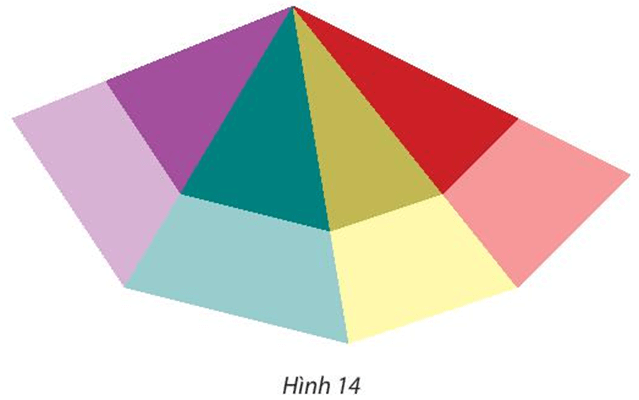
86 lượt xemTrong Hình 14, tìm phép vị tự được dùng để biến bốn tam giác nhỏ thành bốn tam giác lớn.
Lời giải
Hướng dẫn giải:
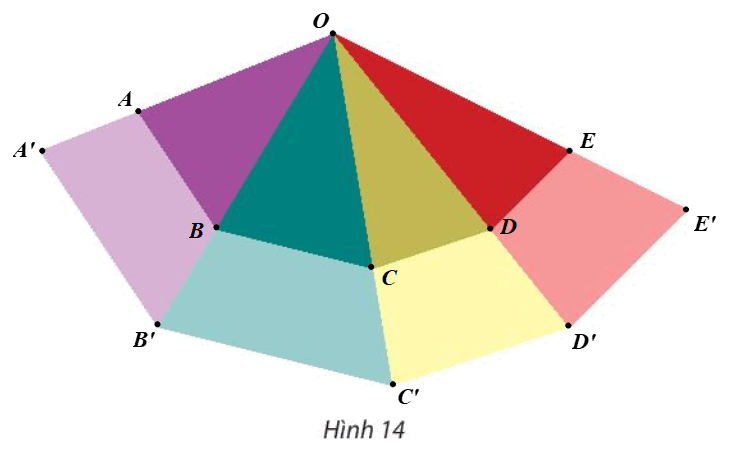
Giả sử ta chọn điểm O như hình vẽ.
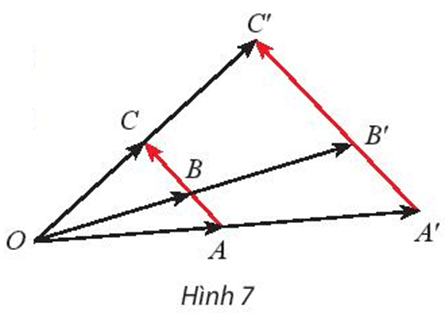
Ta đặt bốn tam giác nhỏ là ∆OAB, ∆OBC, ∆OCD và ∆ODE và bốn tam giác lớn là ∆OA’B’, ∆OB’C’, ∆OC’D’ và ∆OD’E’ (hình vẽ).
Yêu cầu bài toán đưa về tìm phép vị tự biến ∆OAB, ∆OBC, ∆OCD và ∆ODE lần lượt thành ∆OA’B’, ∆OB’C’, ∆OC’D’ và ∆OD’E’.
Tức là ta đi tìm phép vị tự biến các điểm O, A, B, C, D, E lần lượt thành O, A’, B’, C’, D’, E’.
Ta thấy O là giao điểm của các đường thẳng AA’, BB’, CC’, DD’, EE’.
Ta chứng minh các điểm O, A’, B’, C’, D’, E’ lần lượt là ảnh của các điểm O, A, B, C, D, E qua V(O, k).
Thật vậy, ta có V(O, k)(A) = A’.
Suy ra và OA’ = |k|.OA.
Vì A, A’ nằm cùng phía đối với O nên k > 0.
Do đó .
Mà nên , do đó V(O, k)(B) = B’.
Tương tự như trên ta chứng minh được V(O, k)(C) = C’, V(O, k)(D) = D’, V(O, k)(E) = E’.
Vậy là phép vị tự cần tìm.
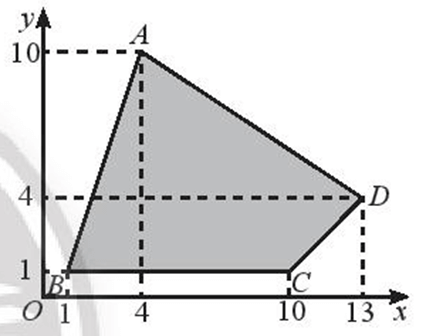
Vẽ Hình 11 ra giấy kẻ ô li và tìm ảnh của tứ giác ABCD qua phép vị tự .