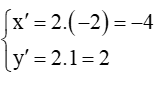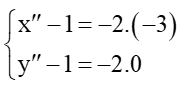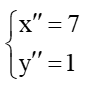Câu hỏi:
93 lượt xemTrong mặt phẳng tọa độ Oxy, cho đường tròn (C) có phương trình:
(C): x2 + y2 + 4x – 2y – 4 = 0.
Viết phương trình ảnh của (C)
a) qua phép vị tự tâm O, tỉ số k = 2;
b) qua phép vị tự tâm I(1; 1), tỉ số k = –2.
Lời giải
Hướng dẫn giải:
Đường tròn (C): x2 + y2 + 4x – 2y – 4 = 0 có tâm A(–2; 1) và bán kính .
a) Gọi đường tròn (C’) là ảnh của đường tròn (C) qua V(O, 2)
Khi đó (C’) có tâm ảnh của A qua V(O, 2) và bán kính R’ = |2|.R = 2.3 = 6.
Gọi A’(x’; y’) là ảnh của A qua V(O, 2).
Suy ra với và
Do đó
Vì vậy A’(–4; 2).
Vậy phương trình đường tròn (C’) là: (x + 4)2 + (y – 2)2 = 36.
b) Gọi đường tròn (C’’) là ảnh của đường tròn (C) qua V(I, –2).
Khi đó (C’’') có tâm ảnh của A qua V(I, –2) và bán kính R’’ = |–2|.R = 2.3 = 6.
Gọi A”(x”; y”) là ảnh của A qua V(I, –2).
Suy ra với và
Do đó
Vì vậy
Suy ra tọa độ A”(7; 1).
Vậy phương trình đường tròn (C”) là: (x – 7)2 + (y – 1)2 = 36.
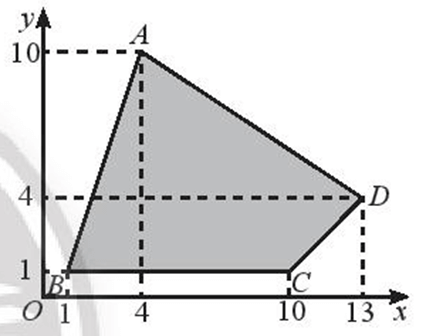
Vẽ Hình 11 ra giấy kẻ ô li và tìm ảnh của tứ giác ABCD qua phép vị tự .