Lý thuyết Bất phương trình bậc hai một ẩn (Cánh diều 2024) Toán 10

Video giải Toán 10 Bài 4: Bất phương trình bậc hai một ẩn - Cánh diều

A. Lý thuyết Bất phương trình bậc hai một ẩn

1. Bất phương trình bậc hai một ẩn

– Bất phương trình bậc hai một ẩn x là bất phương trình có một trong các dạng sau: ax2 + bx + c < 0; ax2 + bx + c ≤ 0; ax2 + bx + c > 0; ax2 + bx + c ≥ 0, trong đó a, b, c là các số thực đã cho, a ≠ 0.

– Đối với bất phương trình bậc hai có dạng ax2 + bx + c < 0, mỗi số x0 ∈ ℝ sao cho ${{\mathrm{ax}}_0}^2+{\mathrm{bx}}_0+\mathrm{c}<0$ được gọi là một nghiệm của bất phương trình đó.

Tập hợp các nghiệm x như thế còn được gọi là tập nghiệm của bất phương trình bậc hai đã cho.

Nghiệm và tập nghiệm của các dạng bất phương trình bậc hai ẩn x còn lại được định nghĩa tương tự.

Ví dụ: Cho bất phương trình bậc hai một ẩn ${\mathrm{x}}^2-3\mathrm{x}+2\le 0$ (1). Trong các giá trị sau đây của x, giá trị nào là nghiệm của bất phương trình (1)?

a) x = 2;                                     

b) x = 0;                                   

 c) x = 3.

Hướng dẫn giải

a) Với x = 2, ta có: 22 – 3.2 + 2 = 0. Vậy x = 2 là nghiệm của bất phương trình (1).

b) Với x = 0, ta có: 02 – 3.0 + 2 = 2 > 0.Vậy x = 0 không phải là nghiệm của bất phương trình (1).

c) Với x = 3, ta có: 32 – 3.3 + 3 > 0. Vậy x = 3 không phải là nghiệm của bất phương trình (1).

Chú ý: Giải bất phương trình bậc hai ẩn x là đi tìm tập nghiệm của bất phương trình đó.

2. Giải bất phương trình bậc hai một ẩn

2.1. Giải bất phương trình bậc hai một ẩn bằng cách xét dấu của tam thức bậc hai

Nhận xét: Để giải bất phương trình bậc hai (một ẩn) có dạng:

 f(x) > 0 (f(x) = ax2 + bx + c), ta chuyển việc giải bất phương trình đó về việc tìm tập hợp những giá trị của x sao cho f(x) mang dấu “+”. Cụ thể, ta làm như sau:

Bước 1. Xác định dấu của hệ số a và tìm nghiệm của f(x) (nếu có).

Bước 2. Sử dụng định lí về dấu của tam thức bậc hai để tìm tập hợp những giá trị của x sao cho f(x) mang dấu “+”.

Chú ý: Các bất phương trình bậc hai có dạng f(x) < 0, f(x) ≥ 0, f(x) ≤ 0 được giải bằng cách tương tự.

Ví dụ: Giải các bất phương trình bậc hai sau:

a) ${\mathrm{x}}^2-5\mathrm{x}+4>0$;

b) $-{\mathrm{x}}^2-3\mathrm{x}+4>0$.

Hướng dẫn giải

a) Tam thức bậc hai ${\mathrm{x}}^2-5\mathrm{x}+4>0$ có hai nghiệm phân biệt ${\mathrm{x}}_1=1$, ${\mathrm{x}}_2=4$ và có hệ số a = 1 > 0. Sử dụng định lí về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của x sao cho tam thức ${\mathrm{x}}^2-5\mathrm{x}+4>0$ mang dấu “+” là $(-\infty ;1)\cup (4;+\infty ).$

Vậy tập nghiệm của bất phương trình ${\mathrm{x}}^2-5\mathrm{x}+4>0$ là $(-\infty ;1)\cup (4;+\infty ).$

b) Tam thức bậc hai $-{\mathrm{x}}^2-3\mathrm{x}+4>0$ có hai nghiệm ${\mathrm{x}}_1=-4$,${\mathrm{x}}_2=1$ và có hệ số $\mathrm{a}=-1<0$.

Sử dụng định lí về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của x sao cho tam thức $-{\mathrm{x}}^2-3\mathrm{x}+4>0$ mang dấu “+” là (– 4; 1).

Vậy tập nghiệm của bất phương trình – x2 – 3x + 4 > 0 là ($-$4; 1).

2.2. Giải bất phương trình bậc hai một ẩn bằng cách sử dụng đồ thị

– Giải bất phương trình bậc hai ax2 + bx + c > 0 là tìm tập hợp những giá trị của x ứng với phần parabol y = ax2 + bx + c nằm phía trên trục hoành.

– Tương tự, giải bất phương trình bậc hai ax2 + bx + c < 0 là tìm tập hợp những giá trị của x ứng với phần parabol y = ax2 + bx + c nằm phía dưới trục hoành.

Như vậy, để giải bất phương trình bậc hai (một ẩn) có dạng:

f(x) > 0 (f(x) = ax2 + bx + c) bằng cách sử dụng đồ thị, ta có thể làm như sau: Dựa vào parabol y = ax2 + bx + c, ta tìm tập hợp những giá trị của x ứng với phần parabol đó nằm phía trên trục hoành. Đối vổi các bất phương trình bậc hai có dạng f(x) < 0, f(x) ≥ 0, ,f(x) ≤ 0, ta cũng làm tương tự.

Ví dụ: Quan sát đồ thị và giải các bất phương trình bậc hai sau:

a) ${\mathrm{x}}^2-3\mathrm{x}+2<0$                                         

 b) $-{\mathrm{x}}^2+2\mathrm{x}$ > 0

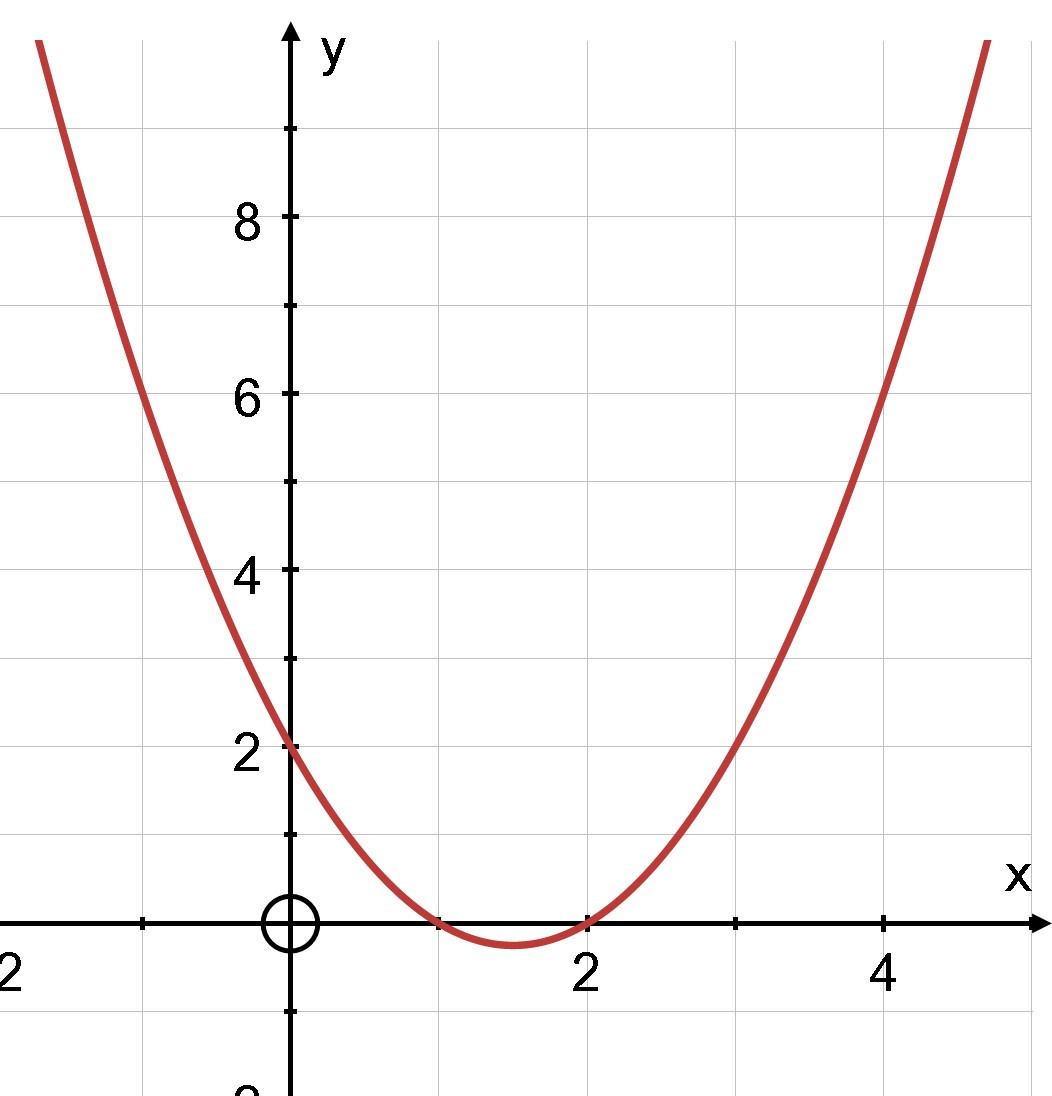
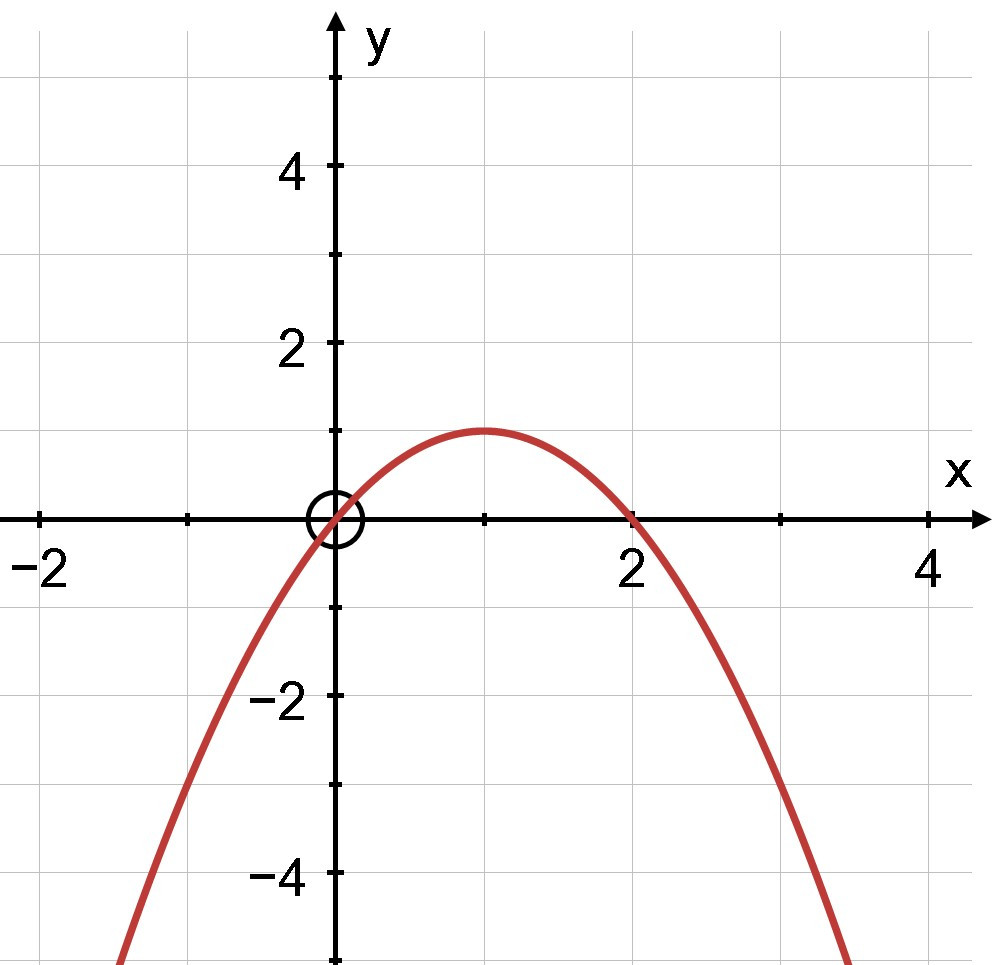
Đồ thị y =${\mathrm{x}}^2-3\mathrm{x}+2$                                                                                    Đồ thị y =$-{\mathrm{x}}^2+2\mathrm{x}$

Hướng dẫn giải

a) Quan sát đồ thị, ta thấy${\mathrm{x}}^2-3\mathrm{x}+2<0$ biểu diễn phần parabol y =${\mathrm{x}}^2-3\mathrm{x}+2$ nằm phía dưới trục hoành, tương ứng với 1 < x < 2.

Vậy tập nghiệm của bất phương trình ${\mathrm{x}}^2-3\mathrm{x}+2<0$ là khoảng (1; 2).

b) Quan sát đồ thị, ta thấy $-{\mathrm{x}}^2+2\mathrm{x}$ > 0 biểu diễn phần parabol y =$-{\mathrm{x}}^2+2\mathrm{x}$ nằm phía trên trục hoành, tương ứng với 0 < x < 2.

Vậy tập nghiệm của bất phương trình $-{\mathrm{x}}^2+2\mathrm{x}$ > 0  là khoảng (0 ; 2).

2.3. Ứng dụng của bất phương trình bậc hai một ẩn

Bất phương trình bậc hai một ẩn có nhiều ứng dụng, chẳng hạn: giải một số hệ bất phương trình; ứng dụng vào tính toán lợi nhuận trong kinh doanh; tính toán điểm rơi trong pháo binh;...

Chúng ta sẽ làm quen với những ứng dụng đó qua một số ví dụ sau đây.

Ví dụ 4: Tìm giao các tập nghiệm của hai bất phương trình sau:

${\mathrm{x}}^2+2\mathrm{x}-3<0$ (3) và ${\mathrm{x}}^2-4\mathrm{x}+3<0$ (4)

Hướng dẫn giải

Ta có: $\left(3\right) \iff -3<\text{x}<1.$ Tập nghiệm của bất phương trình (3) là S3= (−3 ; 1);

$\left(4\right) \iff 1<\text{x}<3.$ Tập nghiệm của bất phương trình (4) là S4= (1 ; 3).

Giao các tập nghiệm của hai bất phương trình trên là:

$\mathrm{S}={\mathrm{S}}_3\cap {\mathrm{S}}_4=\left(-3;1\right)\cap \left(1;3\right)=\varnothing$.

B. Bài tập tự luyện

B.1 Bài tập tự luận

Bài 1. Tìm tổng các nghiệm nguyên của bất phương trình: $\mathrm{x}\left(2-\mathrm{x}\right)\ge \mathrm{x}\left(7-\mathrm{x}\right)-6\left(\mathrm{x}-1\right)$ trên đoạn $\left[-10;10\right]$.

Hướng dẫn giải

Bất phương trình: $\mathrm{x}\left(2-\mathrm{x}\right)\ge \mathrm{x}\left(7-\mathrm{x}\right)-6\left(\mathrm{x}-1\right)$

$\iff 2\mathrm{x}-{\mathrm{x}}^2\ge 7\mathrm{x}-{\mathrm{x}}^2-6\mathrm{x}+6\iff \mathrm{x}\ge 6\underset{\mathrm{x}\in \mathrm{\mathbb{Z}}}{\overset{\mathrm{x}\in \left[-10;10\right]}{\to }}\mathrm{x}\in \left\{6;7;8;9;10\right\}$.

Tổng tất cả các nghiệm là: 6 + 7 + 8 + 9 + 10 = 40.

Bài 2. Tìm tập nghiệm của bất phương trình: $\sqrt{2}{\mathrm{x}}^2-\left(\sqrt{2}+1\right)\mathrm{x}+1<0$.

Hướng dẫn giải

Ta có: $\mathrm{f}\left(\mathrm{x}\right)=\sqrt{2}{\mathrm{x}}^2-\left(\sqrt{2}+1\right)\mathrm{x}+1=0\iff \left[\begin{array}{l}\mathrm{x}=\frac{\sqrt{2}}{2}\\ \mathrm{x}=1\end{array}\right.$.

Bảng xét dấu

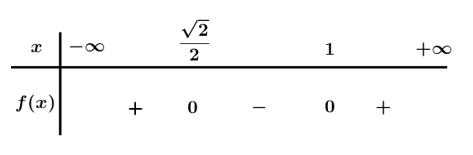
Dựa vào bảng xét dấu $\mathrm{f}\left(\mathrm{x}\right)<0\iff \frac{\sqrt{2}}{2}<\mathrm{x}<1$.

B.2 Bài tập trắc nghiệm

Câu 1. Tập nghiệm của bất phương trình: $–{\mathrm{x}}^2+6\mathrm{x}+7 \ge 0$là:

A. $\left(-\infty ;-1\right]\cup \left[7;+\infty \right)$;                   

B. $\left[-1;7\right]$;          

C. $\left(-\infty ;-7\right]\cup \left[1;+\infty \right)$;                   

D. $\left[-7;1\right]$.

Hướng dẫn giải

Đáp án đúng là: B

Ta có: f(x) = $–{\mathrm{x}}^2+6\mathrm{x}+7 =0\iff \left[\begin{array}{l}\mathrm{x}=7\\ \mathrm{x}=-1\end{array}\right.$.

Bảng xét dấu

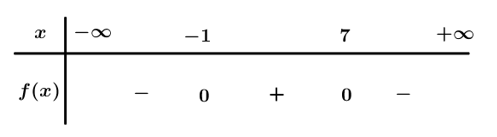
Dựa vào bảng xét dấu $–{\mathrm{x}}^2+6\mathrm{x}+7 \ge 0\iff -1\le \mathrm{x}\le 7.$ 

Câu 2. Số thực dương x lớn nhất thỏa mãn ${\mathrm{x}}^2-\mathrm{x}-12\le 0$ là?

A. 1;

B. 2;

C. 3;  

D. 4.  

Hướng dẫn giải

Đáp án đúng là: D

Ta có $\mathrm{f}\left(\mathrm{x}\right)={\mathrm{x}}^2-\mathrm{x}-12=0\iff \left[\begin{array}{l}\mathrm{x}=4\\ \mathrm{x}=-3\end{array}\right.$.

Bảng xét dấu

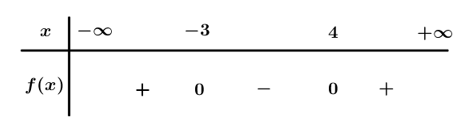
Dựa vào bảng xét dấu $\mathrm{f}\left(\mathrm{x}\right)\le 0\iff -3\le \mathrm{x}\le 4$. Suy ra số thực dương x lớn nhất thỏa ${\mathrm{x}}^2-\mathrm{x}-12\le 0$ là 4.

Câu 3. Giải bất phương trình $\mathrm{x}\left(\mathrm{x}+5\right)\le 2\left({\mathrm{x}}^2+2\right).$

A. $\mathrm{x}\le 1;$             

B. $1\le \mathrm{x}\le 4;$        

C. $\mathrm{x}\in \left(-\infty ;1\right]\cup \left[4;+\infty \right);$     

D. $\mathrm{x}\ge 4.$

Hướng dẫn giải

Đáp án đúng là: C

Bất phương trình $\mathrm{x}\left(\mathrm{x}+5\right)\le 2\left({\mathrm{x}}^2+2\right)\iff {\mathrm{x}}^2+5\mathrm{x}\le 2{\mathrm{x}}^2+4\iff {\mathrm{x}}^2-5\mathrm{x}+4\ge 0$

Xét phương trình ${\mathrm{x}}^2-5\mathrm{x}+4=0\iff \left(\mathrm{x}-1\right)\left(\mathrm{x}-4\right)=0\iff \left[\begin{array}{l}\mathrm{x}=1\\ \mathrm{x}=4\end{array}\right..$ 

Lập bảng xét dấu

Dựa vào bảng xét dấu, ta thấy ${\mathrm{x}}^2-5\mathrm{x}+4\ge 0\iff \mathrm{x}\in \left(-\infty ;1\right]\cup \left[4;+\infty \right).$