Lý thuyết Tổng và hiệu của hai vectơ (Cánh diều 2024) Toán 10

Lý thuyết Toán lớp 10 Bài 4: Tổng và hiệu của hai vectơ

Video giải Toán 10 Bài 4: Tổng và hiệu của hai vectơ - Cánh diều

A. Lý thuyết Tổng và hiệu của hai vectơ

1. Tổng của hai vectơ

1.1. Định nghĩa

– Với ba điểm bất kì A, B, C, vectơ $\overrightarrow{\mathrm{AC}}$ được gọi là tổng của hai vectơ $\overrightarrow{\mathrm{AB}}$ và $\overrightarrow{\mathrm{BC}}$, kí hiệu là $\overrightarrow{\mathrm{AC}}$ = $\overrightarrow{\mathrm{AB}}$ + $\overrightarrow{\mathrm{BC}}$.

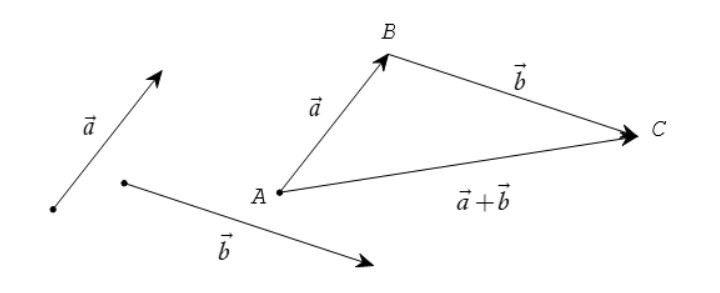
– Cho hai vectơ $\overrightarrow{\mathrm{a}}$ và $\overrightarrow{\mathrm{b}}$. Lấy một điểm A tùy ý, vẽ $\overrightarrow{\mathrm{AB}}$= $\overrightarrow{\mathrm{a}}$ và $\overrightarrow{\mathrm{BC}}$= $\overrightarrow{\mathrm{b}}$. Vectơ $\overrightarrow{\mathrm{AB}}$ được gọi là tổng của hai vectơ $\overrightarrow{\mathrm{a}}$ và $\overrightarrow{\mathrm{b}}$. Ta kí hiệu tổng của hai vectơ $\overrightarrow{\mathrm{a}}$ và $\overrightarrow{\mathrm{b}}$ là $\overrightarrow{\mathrm{a}}$ + $\overrightarrow{\mathrm{b}}$. Vậy $\overrightarrow{\mathrm{AC}}$ = $\overrightarrow{\mathrm{a}}$ + $\overrightarrow{\mathrm{b}}$.

Phép lấy tổng của hai vectơ còn được gọi là phép cộng vectơ.

Ví dụ: Cho hình chữ nhật ABCD tâm O. Tính:

a) $\overrightarrow{\mathrm{OA}}$+ $\overrightarrow{\mathrm{DC}}$

b) $\overrightarrow{\mathrm{BC}}$ + $\overrightarrow{\mathrm{OA}}$

Hướng dẫn giải:

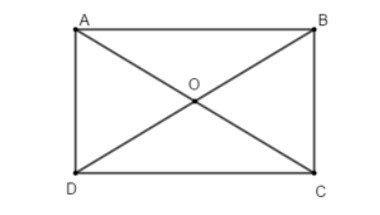
a) Vì ABCD là hình chữ nhật nên AB // CD và AB = CD.

⇒ $\overrightarrow{\mathrm{DC}}$ = $\overrightarrow{\mathrm{AB}}$.

⇒ $\overrightarrow{\mathrm{OA}}$+ $\overrightarrow{\mathrm{DC}}$ = $\overrightarrow{\mathrm{OA}}$+ $\overrightarrow{\mathrm{AB}}$= $\overrightarrow{\mathrm{OB}}$.

b) Vì A, O, C thẳng hàng (O là trung điểm của đường chéo AC)

⇒ $\overrightarrow{\mathrm{OA}}$= $\overrightarrow{\mathrm{CO}}$.

⇒ $\overrightarrow{\mathrm{BC}}$ + $\overrightarrow{\mathrm{OA}}$= $\overrightarrow{\mathrm{BC}}$ + $\overrightarrow{\mathrm{CO}}$ = $\overrightarrow{\mathrm{BO}}$.

1.2. Quy tắc hình bình hành

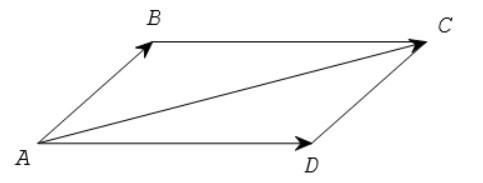
Nếu ABCD là hình bình hành thì $\overrightarrow{\mathrm{AB}}$+$\overrightarrow{\mathrm{AD}}$= $\overrightarrow{\mathrm{AC}}$.

Ví dụ: Chứng minh quy tắc hình bình hành.

Hướng dẫn giải:

Ta có: $\overrightarrow{\mathrm{AD}}$= $\overrightarrow{\mathrm{BC}}$.

Suy ra: $\overrightarrow{\mathrm{AB}}$+$\overrightarrow{\mathrm{AD}}$= $\overrightarrow{\mathrm{AB}}$+ $\overrightarrow{\mathrm{BC}}$= $\overrightarrow{\mathrm{AC}}$.

1.3. Tính chất

Với ba vectơ tùy ý $\overrightarrow{\mathrm{a}}$, $\overrightarrow{\mathrm{b}}$, $\overrightarrow{\mathrm{c}}$ ta có:

$\overrightarrow{\mathrm{a}}$ + $\overrightarrow{\mathrm{b}}$ = $\overrightarrow{\mathrm{b}}$ + $\overrightarrow{\mathrm{a}}$ (tính chất giao hoán) ;

($\overrightarrow{\mathrm{a}}$ + $\overrightarrow{\mathrm{b}}$) + $\overrightarrow{\mathrm{c}}$ = $\overrightarrow{\mathrm{a}}$ + ($\overrightarrow{\mathrm{b}}$ + $\overrightarrow{\mathrm{c}}$) (tính chất kết hợp);

$\overrightarrow{\mathrm{a}}$ + $\overrightarrow{0}$ = $\overrightarrow{0}$ + $\overrightarrow{\mathrm{a}}$ = $\overrightarrow{\mathrm{a}}$ (tính chất của vectơ–không).

Chú ý: Tổng ba vectơ $\overrightarrow{\mathrm{a}}$ + $\overrightarrow{\mathrm{b}}$ + $\overrightarrow{\mathrm{c}}$ được xác định theo một trong hai cách sau:

($\overrightarrow{\mathrm{a}}$ + $\overrightarrow{\mathrm{b}}$) + $\overrightarrow{\mathrm{c}}$ hoặc $\overrightarrow{\mathrm{a}}$ + ($\overrightarrow{\mathrm{b}}$ + $\overrightarrow{\mathrm{c}}$).

Ví dụ: Cho 5 điểm tùy ý A, B, C, D, E. Chứng minh rằng:

a) $\overrightarrow{\mathrm{CD}}+\overrightarrow{\mathrm{EC}}+\overrightarrow{\mathrm{DA}}+\overrightarrow{\mathrm{BE}}$ = $\overrightarrow{\mathrm{BA}}$.

b) $\overrightarrow{\mathrm{AB}}$+ $\overrightarrow{\mathrm{CD}}$+ $\overrightarrow{\mathrm{EA}}$= $\overrightarrow{\mathrm{CB}}$ + $\overrightarrow{\mathrm{ED}}$.

Hướng dẫn giải:

a) Ta có:

$\overrightarrow{\mathrm{CD}}+\overrightarrow{\mathrm{EC}}+\overrightarrow{\mathrm{DA}}+\overrightarrow{\mathrm{BE}}$ 

= $\overrightarrow{\mathrm{CD}}+\overrightarrow{\mathrm{DA}}+\overrightarrow{\mathrm{BE}}+\overrightarrow{\mathrm{EC}}$              (áp dụng tính chất giao hoán)

= $\left(\overrightarrow{\mathrm{CD}}+\overrightarrow{\mathrm{DA}}\right)+\left(\overrightarrow{\mathrm{BE}}+\overrightarrow{\mathrm{EC}}\right)$        (áp dụng tính chất kết hợp)

= $\overrightarrow{\mathrm{CA}}+\overrightarrow{\mathrm{BC}}$  (áp dụng quy tắc cộng vectơ)

= $\overrightarrow{\mathrm{BC}}+\overrightarrow{\mathrm{CA}}$  (áp dụng tính chất giao hoán)

= $\overrightarrow{\mathrm{BA}}$ (áp dụng quy tắc cộng vectơ) (đpcm).

Vậy $\overrightarrow{\mathrm{CD}}+\overrightarrow{\mathrm{EC}}+\overrightarrow{\mathrm{DA}}+\overrightarrow{\mathrm{BE}}$ = $\overrightarrow{\mathrm{BA}}$.

b) Ta có:

$\overrightarrow{\mathrm{AB}}$+ $\overrightarrow{\mathrm{CD}}$+ $\overrightarrow{\mathrm{EA}}$

= $\left(\overrightarrow{\mathrm{AC}}+\overrightarrow{\mathrm{CB}}\right)+\overrightarrow{\mathrm{CD}}+\left(\overrightarrow{\mathrm{ED}}+\overrightarrow{\mathrm{DA}}\right)$         (áp dụng quy tắc cộng vectơ)

= $\overrightarrow{\mathrm{CB}}+\overrightarrow{\mathrm{ED}}+\overrightarrow{\mathrm{AC}}+\overrightarrow{\mathrm{CD}}+\overrightarrow{\mathrm{DA}}$               (áp dụng tính chất giao hoán)

= $\overrightarrow{\mathrm{CB}}+\overrightarrow{\mathrm{ED}}+\left(\overrightarrow{\mathrm{AC}}+\overrightarrow{\mathrm{CD}}\right)+\overrightarrow{\mathrm{DA}}$  (áp dụng tính chất kết hợp)

= $\overrightarrow{\mathrm{CB}}+\overrightarrow{\mathrm{ED}}+\stackrel{\rightharpoonup }{\mathrm{AD}}+\overrightarrow{\mathrm{DA}}$             (áp dụng quy tắc cộng vectơ)

= $\overrightarrow{\mathrm{CB}}+\overrightarrow{\mathrm{ED}}+\left(\stackrel{\rightharpoonup }{\mathrm{AD}}+\overrightarrow{\mathrm{DA}}\right)$           (áp dụng tính chất kết hợp)

= $\overrightarrow{\mathrm{CB}}+\overrightarrow{\mathrm{ED}}+\overrightarrow{\mathrm{AA}}$ 

= $\overrightarrow{\mathrm{CB}}+\overrightarrow{\mathrm{ED}}+\overrightarrow{0}$      (vectơ có điểm đầu và điểm cuối trùng nhau là vectơ–không)

= $\overrightarrow{\mathrm{CB}}+\overrightarrow{\mathrm{ED}}$            (áp dụng tính chất vectơ–không) (đpcm).

2. Hiệu của hai vectơ

2.1. Hai vectơ đối nhau

Định nghĩa: Vectơ có cùng độ dài và ngược hướng với vectơ $\overrightarrow{\mathrm{a}}$ được gọi là vectơ đối của vectơ $\overrightarrow{\mathrm{a}}$, kí hiệu là –$\overrightarrow{\mathrm{a}}$. Hai vectơ $\overrightarrow{\mathrm{a}}$ và –$\overrightarrow{\mathrm{a}}$ được gọi là hai vectơ đối nhau.

Quy ước: Vectơ đối của vectơ $\overrightarrow{0}$ là vectơ $\overrightarrow{0}$.

Nhận xét:

+) $\overrightarrow{\mathrm{a}}$ + (–$\overrightarrow{\mathrm{a}}$) = (–$\overrightarrow{\mathrm{a}}$) + $\overrightarrow{\mathrm{a}}$ = $\overrightarrow{0}$

+) Hai vectơ $\overrightarrow{\mathrm{a}}$, $\overrightarrow{\mathrm{b}}$ là hai vectơ đối nhau khi và chỉ khi $\overrightarrow{\mathrm{a}}$ + $\overrightarrow{\mathrm{b}}$ = $\overrightarrow{0}$.

+) Với hai điểm A, B, ta có: $\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{BA}}=\overrightarrow{0}$.

Lưu ý: Cho hai điểm A, B. Khi đó hai vectơ $\overrightarrow{\mathrm{AB}}$ và $\overrightarrow{\mathrm{BA}}$ là hai vectơ đối nhau, tức là $\overrightarrow{\mathrm{BA}}=-\overrightarrow{\mathrm{AB}}.$  

Chú ý:

– I là trung điểm của đoạn thẳng AB khi và chỉ khi $\overrightarrow{\mathrm{IA}}+\overrightarrow{\mathrm{IB}}=\overrightarrow{0}$.

– G là trọng tâm của tam giác ABC khi và chỉ khi $\overrightarrow{\mathrm{GA}}+\overrightarrow{\mathrm{GB}}+\overrightarrow{\mathrm{GC}}=\overrightarrow{0}$.

Ví dụ: Cho hình vuông ABCD có tâm O. Tìm vectơ đối của các vectơ $\overrightarrow{\mathrm{AB}}$, $\overrightarrow{\mathrm{AO}}$.

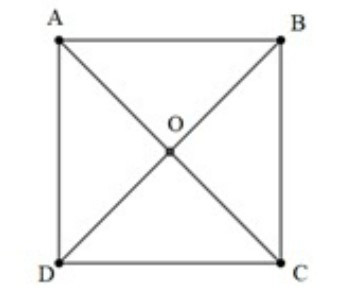
Hướng dẫn giải:

+ Vì $\left|\overrightarrow{\mathrm{BA}}\right|=\left|\overrightarrow{\mathrm{AB}}\right|$= AB và $\overrightarrow{\mathrm{BA}}$ ngược hướng với  $\overrightarrow{\mathrm{AB}}$

⇒ $\overrightarrow{\mathrm{BA}}$ = –$\overrightarrow{\mathrm{AB}}$

Þ $\overrightarrow{\mathrm{BA}}$ là vectơ đối của vectơ $\overrightarrow{\mathrm{AB}}$.

+ Vì AB = CD, AB // CD (ABCD là hình vuông)

⇒ $\left|\overrightarrow{\mathrm{AB}}\right|=\left|\overrightarrow{\mathrm{CD}}\right|$ và $\overrightarrow{\mathrm{CD}}$ ngược hướng với $\overrightarrow{\mathrm{AB}}$

⇒ $\overrightarrow{\mathrm{CD}}$ = –$\overrightarrow{\mathrm{AB}}$

Þ $\overrightarrow{\mathrm{CD}}$ là vectơ đối của vectơ $\overrightarrow{\mathrm{AB}}$.

Vì A, O, C là ba điểm thẳng hàng và OA = OC (ABCD là hình vuông)

⇒ $\overrightarrow{\mathrm{AO}}$ ngược hướng với $\overrightarrow{\mathrm{CO}}$ và $\left|\overrightarrow{\mathrm{AO}}\right|=\left|\overrightarrow{\mathrm{CO}}\right|$

⇒ $\overrightarrow{\mathrm{CO}}$ = –$\overrightarrow{\mathrm{AO}}$

Þ $\overrightarrow{\mathrm{CO}}$ là vectơ đối của $\overrightarrow{\mathrm{AO}}$.

Vậy $\overrightarrow{\mathrm{BA}}$, $\overrightarrow{\mathrm{CD}}$ là vectơ đối của vectơ $\overrightarrow{\mathrm{AB}}$ và $\overrightarrow{\mathrm{CO}}$ là vectơ đối của $\overrightarrow{\mathrm{AO}}$.

2.2. Hiệu của hai vectơ

Hiệu của hai vectơ $\overrightarrow{\mathrm{a}}$ và $\overrightarrow{\mathrm{b}}$, kí hiệu là $\overrightarrow{\mathrm{a}}$ – $\overrightarrow{\mathrm{b}}$, là tổng của vectơ $\overrightarrow{\mathrm{a}}$ và vectơ đối của vectơ $\overrightarrow{\mathrm{b}}$, tức là $\overrightarrow{\mathrm{a}}$ – $\overrightarrow{\mathrm{b}}$ = $\overrightarrow{\mathrm{a}}$ + (–$\overrightarrow{\mathrm{b}}$).

Phép lấy hiệu của hai vectơ được gọi là phép trừ hai vectơ.

Nhận xét: Với ba điểm bất kì A, B, O ta có: $\overrightarrow{\mathrm{AB}}$ = $\overrightarrow{\mathrm{OB}}-\overrightarrow{\mathrm{OA}}$.

Ví dụ: Cho 4 điểm A, B, C, D phân biệt. Chứng minh rằng:

$\overrightarrow{\mathrm{AB}}$ – $\overrightarrow{\mathrm{AD}}$ = $\overrightarrow{\mathrm{DC}}-\overrightarrow{\mathrm{BC}}$

Hướng dẫn giải:

Ta có:

$\overrightarrow{\mathrm{AB}}$ – $\overrightarrow{\mathrm{AD}}$ = $\overrightarrow{\mathrm{DB}}$             (áp dụng quy tắc về hiệu hai vectơ) (1)

$\overrightarrow{\mathrm{DC}}-\overrightarrow{\mathrm{BC}}$ = $\overrightarrow{\mathrm{DC}}+\left(-\overrightarrow{\mathrm{BC}}\right)$ = $\overrightarrow{\mathrm{DC}}+\overrightarrow{\mathrm{CB}}$ = $\overrightarrow{\mathrm{DB}}$           (vectơ đối) (2)

Từ (1) và (2) suy ra: $\overrightarrow{\mathrm{AB}}$ – $\overrightarrow{\mathrm{AD}}$ = $\overrightarrow{\mathrm{DC}}-\overrightarrow{\mathrm{BC}}$ (đpcm).

B. Bài tập tự luyện

B.1 Bài tập tự luận

Bài 1. Cho tam giác ABC có G là trọng tâm của tam giác.

Tính độ dài vectơ $\overrightarrow{\mathrm{GA}}+\overrightarrow{\mathrm{GB}}+\overrightarrow{\mathrm{GC}}$.

Hướng dẫn giải:

Vì G là trọng tâm tam giác ABC nên ta áp dụng quy tắc trọng tâm có:

$\overrightarrow{\mathrm{GA}}+\overrightarrow{\mathrm{GB}}+\overrightarrow{\mathrm{GC}}=\overrightarrow{0}$

⇒ $\left|\overrightarrow{\mathrm{GA}}+\overrightarrow{\mathrm{GB}}+\overrightarrow{\mathrm{GC}}\right|=\left|\overrightarrow{0}\right|=0$

Vậy độ dài vectơ $\overrightarrow{\mathrm{GA}}+\overrightarrow{\mathrm{GB}}+\overrightarrow{\mathrm{GC}}$ là 0.

Bài 2. Cho hình vuông ABCD tâm O. Tính tổng $\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{CB}}$ và $\overrightarrow{\mathrm{CO}}+\overrightarrow{\mathrm{AD}}$.

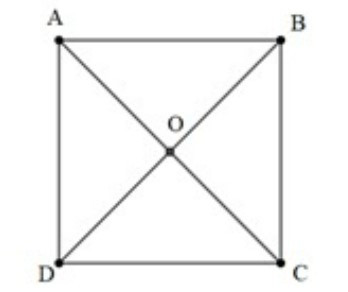
Hướng dẫn giải:

+ Vì ABCD là hình vuông nên AB // DC và AB = DC.

⇒ $\overrightarrow{\mathrm{AB}}=\overrightarrow{\mathrm{DC}}$

⇒ $\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{CB}}=\overrightarrow{\mathrm{DC}}+\overrightarrow{\mathrm{CB}}$

Áp dụng quy tắc cộng hai vectơ ta có:

$\overrightarrow{\mathrm{DC}}+\overrightarrow{\mathrm{CB}}=\overrightarrow{\mathrm{DB}}$

Do đó, $\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{CB}}$= $\overrightarrow{\mathrm{DB}}$.

+ Vì A, O, C cùng nằm trên một đường thẳng và OA = OC (O là tâm hình vuông ABCD).

⇒ $\overrightarrow{\mathrm{CO}}=\overrightarrow{\mathrm{OA}}$

⇒ $\overrightarrow{\mathrm{CO}}+\overrightarrow{\mathrm{AD}}=\overrightarrow{\mathrm{OA}}+\overrightarrow{\mathrm{AD}}$

Áp dụng quy tắc công hai vectơ ta có:

$\overrightarrow{\mathrm{OA}}+\overrightarrow{\mathrm{AD}}=\overrightarrow{\mathrm{OD}}$

Vậy $\overrightarrow{\mathrm{CO}}+\overrightarrow{\mathrm{AD}}$ = $\overrightarrow{\mathrm{OD}}$.

B.2 Bài tập trắc nghiệm

Câu 1. Cho ba điểm phân biệt A, B, C. Đẳng thức nào sau đây đúng?

A. $\overrightarrow{\mathrm{CA}}-\overrightarrow{\mathrm{BA}}=\overrightarrow{\mathrm{BC}};$                                                     

B. $\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{AC}}=\overrightarrow{\mathrm{BC}};$

C. $\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{CA}}=\overrightarrow{\mathrm{CB}};$                                                     

D. $\overrightarrow{\mathrm{AB}}-\overrightarrow{\mathrm{BC}}=\overrightarrow{\mathrm{CA}}.$

Hướng dẫn giải

Đáp án đúng là: C

Xét các đáp án:

- Đáp án A. Ta có $\overrightarrow{\mathrm{CA}}-\overrightarrow{\mathrm{BA}}=\overrightarrow{\mathrm{CA}}+\overrightarrow{\mathrm{AB}}=\overrightarrow{\mathrm{CB}}=-\overrightarrow{\mathrm{BC}}$. Vậy A sai.

- Đáp án B sai vì $\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{BC}}=\overrightarrow{\mathrm{AC}}\Rightarrow \overrightarrow{\mathrm{BC}}=\overrightarrow{\mathrm{AC}}-\overrightarrow{\mathrm{AB}}$$\ne \overrightarrow{\mathrm{AC}}+\overrightarrow{\mathrm{AB}}$.

- Đáp án C. Ta có $\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{CA}}=\overrightarrow{\mathrm{CA}}+\overrightarrow{\mathrm{AB}}=\overrightarrow{\mathrm{CB}}$. Vậy C đúng.

Câu 2. Cho 5 điểm bất kỳ A, B, C, D, E. Tính tổng $\overrightarrow{\mathrm{CD}}+\overrightarrow{\mathrm{EC}}+\overrightarrow{\mathrm{DA}}+\overrightarrow{\mathrm{BE}}$.

A. $\overrightarrow{\mathrm{BC}}$; 

B. $\overrightarrow{\mathrm{CA}}$;

C. $\overrightarrow{\mathrm{EC}}$;               

D. $\overrightarrow{\mathrm{BA}}$.

Hướng dẫn giải

Đáp án đúng là: D

$\overrightarrow{\mathrm{CD}}+\overrightarrow{\mathrm{EC}}+\overrightarrow{\mathrm{DA}}+\overrightarrow{\mathrm{BE}}$ 

= $(\overrightarrow{\mathrm{CD}}+\overrightarrow{\mathrm{DA}})+(\overrightarrow{\mathrm{BE}}+\overrightarrow{\mathrm{EC}})$         (tính chất giao hoán và kết hợp)

= $\overrightarrow{\mathrm{CA}}+\overrightarrow{\mathrm{BC}}$          (quy tắc ba điểm)

= $\overrightarrow{\mathrm{BC}}+\overrightarrow{\mathrm{CA}}$          (tính chất giao hoán)

= $\overrightarrow{\mathrm{BA}}$.

Câu 3. Cho hình bình hành ABCD tâm O. Khi đó, $\overrightarrow{\mathrm{OA}}+\overrightarrow{\mathrm{BO}}=?$

A. $\overrightarrow{\mathrm{OC}}+\overrightarrow{\mathrm{OB}}$;

B. $\overrightarrow{\mathrm{AB}}$;

C. $\overrightarrow{\mathrm{OC}}+\overrightarrow{\mathrm{DO}}$;

D. $\overrightarrow{\mathrm{CD}}$.

Hướng dẫn giải:

Đáp án đúng là: D.

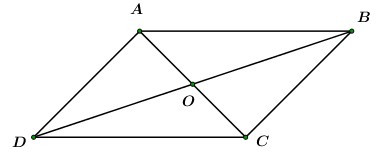
Áp dụng tính chất giao hoán và quy tắc ba điểm cho ba điểm A, O, B ta có:  $\overrightarrow{\mathrm{OA}}+\overrightarrow{\mathrm{BO}}=\overrightarrow{\mathrm{BO}}+\overrightarrow{\mathrm{OA}}=\overrightarrow{\mathrm{BA}}$.

Xét hình bình hành ABCD có: $\overrightarrow{\mathrm{BA}}=\overrightarrow{\mathrm{CD}}$

Vậy $\overrightarrow{\mathrm{OA}}+\overrightarrow{\mathrm{BO}}=\overrightarrow{\mathrm{CD}}$.