Lý thuyết Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụng (Cánh diều 2024) Toán 10
Tóm tắt lý thuyết Toán 10 Bài 2: Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụng ngắn gọn, chính xác sách Kết nối tri thức sẽ giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt Toán 10.
Lý thuyết Toán lớp 10 Bài 2: Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụng
Video giải Toán 10 Bài 2: Hàm số bậc hai. Đồ thị hàm số bậc hai - Cánh diều
A. Lý thuyết Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụng
1. Hàm số bậc hai
Hàm số bậc hai là hàm số được cho bằng biểu thức có dạng y = ax2+bx+cax2+bx+c, trong đó a, b, c là những hằng số và a ≠ 0. Tập xác định của hàm số là ℝ.
Ví dụ:
– Hàm số y = 2x2+3x−22x2+3x−2 là hàm số bậc hai có hệ số của x2 bằng 2, hệ số của x bằng 3 và hệ số tự do bằng –2.
– Hàm số y = 2x – 3 không phải là hàm số bậc số do hệ số của x2 ở đây bằng 0.
2. Đồ thị hàm số bậc hai
Đồ thị hàm số bậc hai y = ax2+bx+cax2+bx+c (a ≠ 0) là một đường parabol có đỉnh là điểm với toạ độ (−b2a;−Δ4a)(−b2a;−Δ4a) và trục đối xứng là đường thẳng x=−b2ax=−b2a.
Chú ý: Cho hàm số f(x) = ax2+bx+cax2+bx+c (a ≠ 0), ta có: −Δ4a−Δ4a = f(−b2a)(−b2a)
Để vẽ đồ thị hàm số y = ax2+bx+cax2+bx+c (a ≠ 0) ta thực hiện các bước:
Bước 1: Xác định toạ độ đỉnh: (−b2a;−Δ4a)(−b2a;−Δ4a);
Bước 2: Vẽ trục đối xứng x=−b2ax=−b2a;
Bước 3: Xác định một số điểm đặc biệt, chẳng hạn: giao điểm với trục tung (có toạ độ (0; c)) và trục hoành (nếu có), điểm đối xứng với điểm có toạ độ (0; c) qua trục đối xứng x=−b2ax=−b2a
Bước 4: Vẽ đường parabol đi qua các điểm đã xác định ta nhận được đồ thị hàm số.
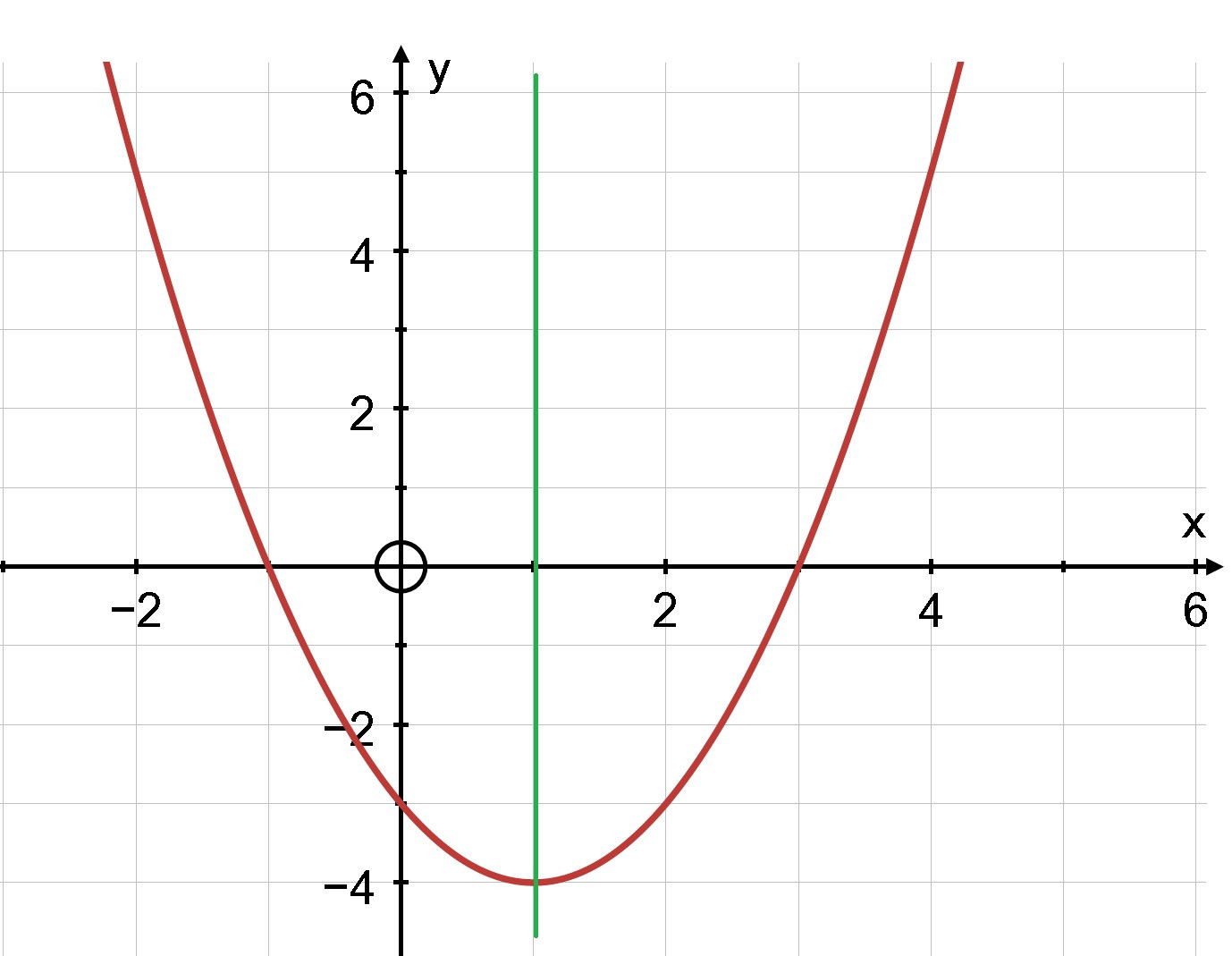
Ví dụ: Vẽ đồ thị hàm số bậc hai y = x2−2x−3x2−2x−3
Hướng dẫn giải
– Tập xác định: D = ℝ
– Ta có: a = 1; b = –2; c = –3; Δ=b2−4acΔ=b2−4ac = (−2)2(−2)2– 4.1.(–3) = 16
– Toạ độ đỉnh I = (−b2a;−Δ4a)(−b2a;−Δ4a) = (22.1;−164.1)=(1;−4)(22.1;−164.1)=(1;−4)
– Trục đối xứng x=−b2ax=−b2a= 1
– Giao điểm của parabol với trục Oy là A(0; –3)
– Giao điểm của parabol với trục Ox là B (–1; 0); (3; 0)
– Điểm đối xứng với điểm A qua trục đối xứng x = 1 là D (2; –3)
Vẽ parabol qua các điểm trên:
Chú ý:
Cho hàm số f(x) = ax2+bx+cax2+bx+c (a ≠ 0)
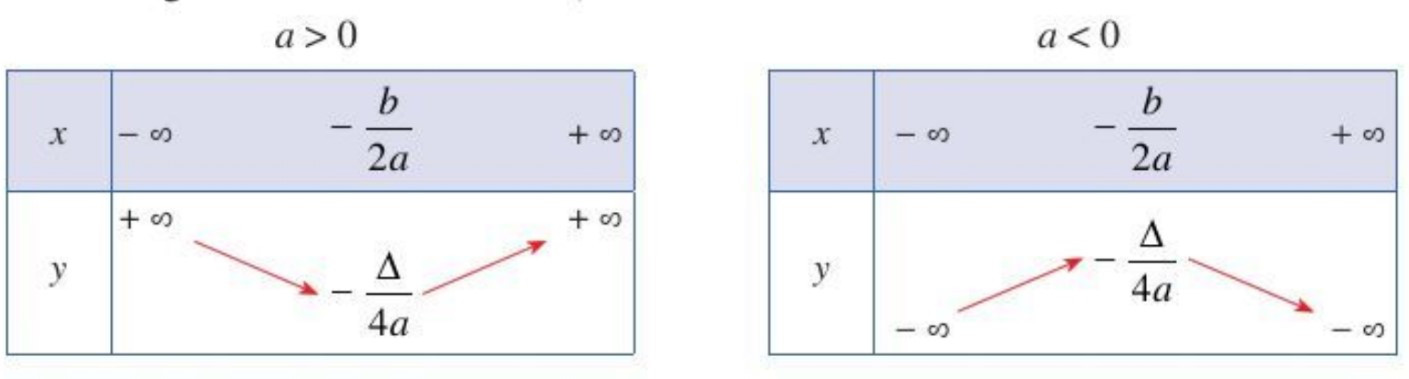
– Nếu a > 0 thì hàm số nghịch biến trên khoảng (−∞;−b2a)(−∞;−b2a); đồng biến trên khoảng (−b2a;+∞)(−b2a;+∞).
– Nếu a < 0 thì hàm số đồng biến trên khoảng (−∞;−b2a)(−∞;−b2a); nghịch biến trên khoảng (−b2a;+∞)(−b2a;+∞).
Bảng biến thiên:
B. Bài tập tự luyện
B.1 Bài tập tự luận
Bài 1. Vẽ đồ thị của mỗi hàm số sau:
a) y = 2x2 – 6x + 4;
b) y = –3x2 – 6x – 3.
Hướng dẫn giải
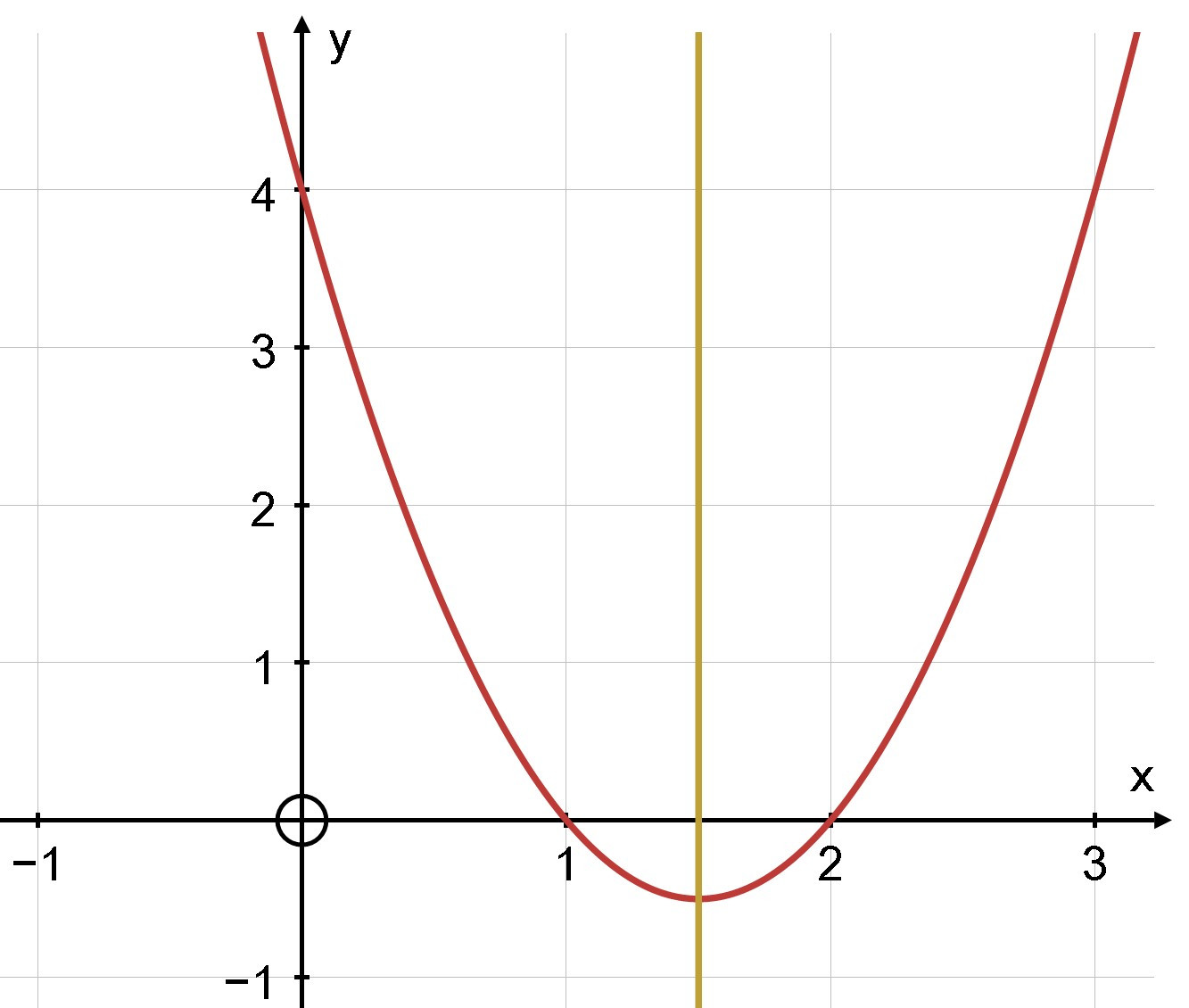
a)
– Tập xác định: D = ℝ
– Ta có: a = 2; b = –6; c = 4; Δ=b2−4acΔ=b2−4ac = (– 6)2 – 4.2.4 = 4
– Toạ độ đỉnh I = (−b2a;−Δ4a)(−b2a;−Δ4a) = (62.2;−44.2)=(32;−12)(62.2;−44.2)=(32;−12)
– Trục đối xứng x=−b2ax=−b2a= 3232
– Giao điểm của parabol với trục Oy là A(0; 4)
– Giao điểm của parabol với trục Ox là B (1; 0); (2; 0)
– Chọn một điểm thuộc đồ thị cho x = –1 thay vào y = 2x2 – 6x + 4 ta được điểm
D(–1; 12)
Vẽ parabol qua các điểm trên:
b)
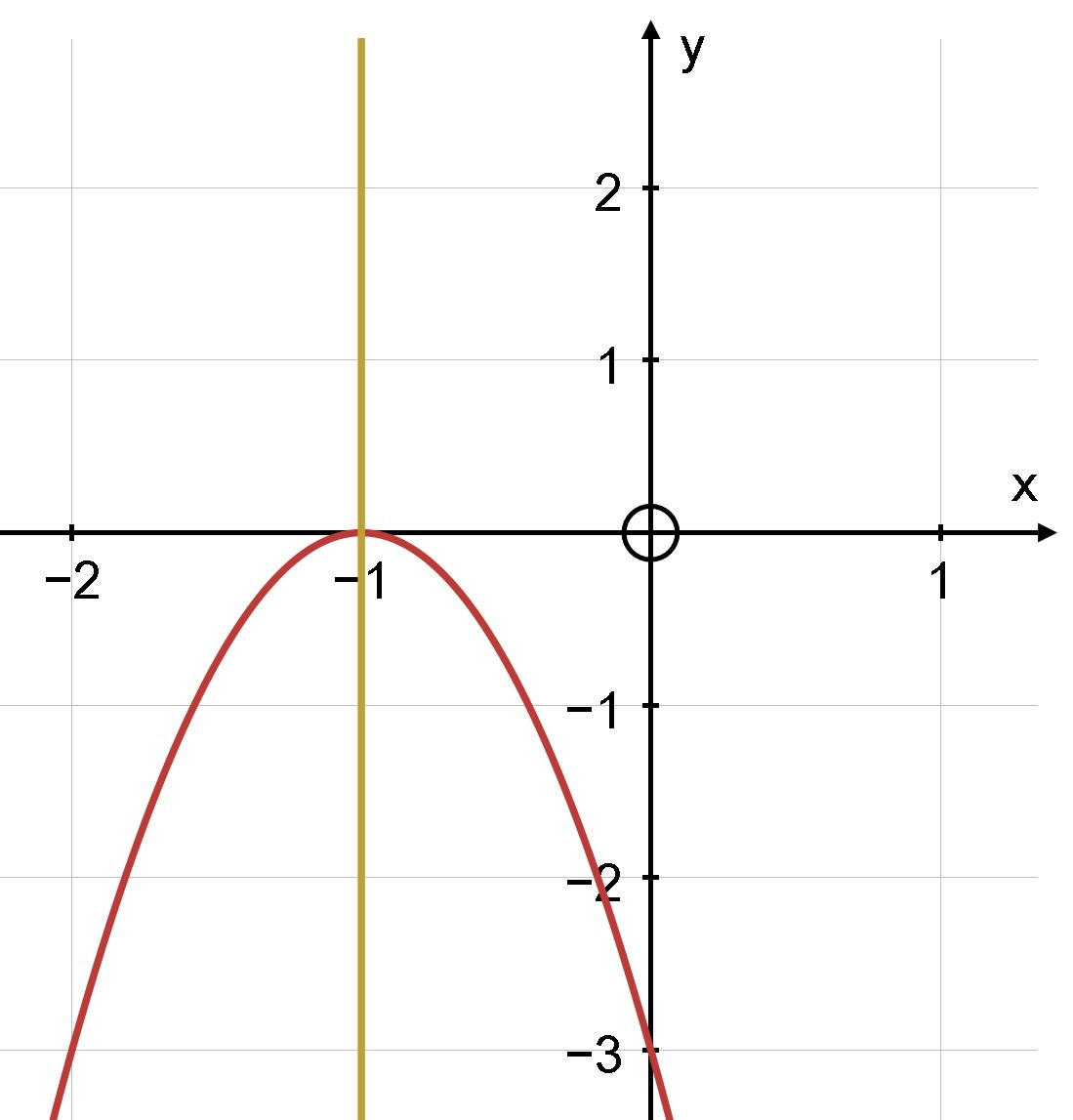
– Tập xác định: D = ℝ
– Ta có: a = –3; b = –6; c = –3; Δ=b2−4acΔ=b2−4ac = (– 6)2 – 4.(–3).(–3) = 0
– Toạ độ đỉnh I = (−b2a;−Δ4a)(−b2a;−Δ4a) = (62.(−3);04.(−3))=(−1;0)(62.(−3);04.(−3))=(−1;0)
– Trục đối xứng x=−b2ax=−b2a= –1
– Giao điểm của parabol với trục Oy là A(0; –3)
– Giao điểm của parabol với trục Ox là B (–1; 0)
– Chọn một điểm thuộc đồ thị cho x = 1 thay vào y = –3x2 – 6x – 3 ta được điểm
D(1; –12)
– Chọn một điểm thuộc đồ thị cho x = –2 thay vào y = –3x2 – 6x – 3 ta được điểm
D(–2; –3)
Vẽ parabol qua các điểm trên:
Bài 2. Xác định parabol y = ax2+bx+4ax2+bx+4 trong mỗi trường hợp sau:
a) Đi qua điểm M(1; 12) và N(–3; 4);
b) Có đỉnh là I(–3; –5).
Hướng dẫn giải
a) Thay x = 1; y = 12 vào phương trình y = ax2+bx+4ax2+bx+4 ta được:
12 = a. 1212+ b.1 + 4 = a + b = 8 (1)
Thay x = –3; y = 4 vào phương trình y = ax2+bx+4ax2+bx+4 ta được:
4 = a.(−3)2(−3)2+ (–3).b + 4 = 9a – 3b = 0 (2)
Từ (1) và (2) ta có: {a+b=89a−3b=0⇔{a=2b=6 . Như vậy y = 2x2+6x+4
b) Ta có: Toạ độ đỉnh I (−b2a;−Δ4a)= (–3; –5)
Δ=b2−4ac= b2 – 4.a.4 = b2 – 16a
{−b2a=−3−b2−16a4a=−5⇔{b−6a=0b2−36a=0⇔{6b−36a=0b2−36a=0⇔b2– 6b = 0 ⇔b(b – 6) = 0
⇔[b=0b=6⇔[a=0a=1. Như vậy trường a = 0; b = 0 không thoả mãn, ta chọn được:
a = 1; b = 6 ⇒ phương trình y = x2 + 6x + 4.
B.2 Bài tập trắc nghiệm
Câu 1. Cho hàm số y=ax2+bx+c(a≠0) có đồ thị như hình sau. Khẳng định nào sau đây đúng?
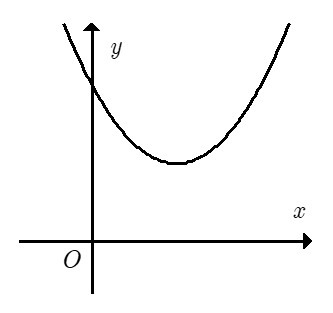
A. a > 0, b < 0, c < 0;
B. a > 0, b < 0, c > 0;
C. a > 0, b > 0, c > 0;
D. a < 0, b < 0, c > 0.
Hướng dẫn giải
Đáp án đúng là: B
Bề lõm hướng lên nên a > 0.
Hoành độ đỉnh parabol x=−b2a>0 nên b < 0.
Parabol cắt trục tung tại điểm có tung độ dương nên c > 0.
Câu 2. Đồ thị sau đây là đồ thị của hàm số nào trong các phương án dưới đây?
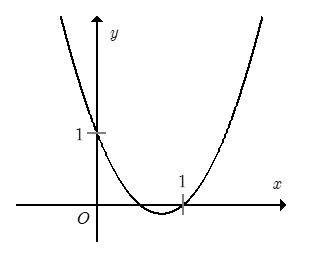
A. y=−x2+3x−1;
B. y=−2x2+3x−1;
C. y=2x2−3x+1;
D. y=x2−3x+1.
Hướng dẫn giải
Đáp án đúng là: C
Parabol có bề lõm hướng lên nên a > 0. Loại đáp án A, B.
Parabol cắt trục hoành tại điểm (1; 0), thay x = 1; y = 0 vào các hàm số ở đáp án C và D:
- Thay x = 1; y = 0 vào y=2x2−3x+1:
0 = 2.12 – 3.1 + 1 (luôn đúng), như vậy điểm (1; 0) thuộc đồ thị hàm số ở đáp án C.
- Thay x = 1; y = 0 vào y=x2−3x+1:
0 = 12 – 3.1 + 1 (vô lí), như vậy điểm (1; 0) không thuộc đồ thị hàm số ở đáp án D.
Câu 3. Bảng biến thiên ở dưới là bảng biến thiên của hàm số nào trong các hàm số được cho ở bốn phương án A, B, C, D sau đây?
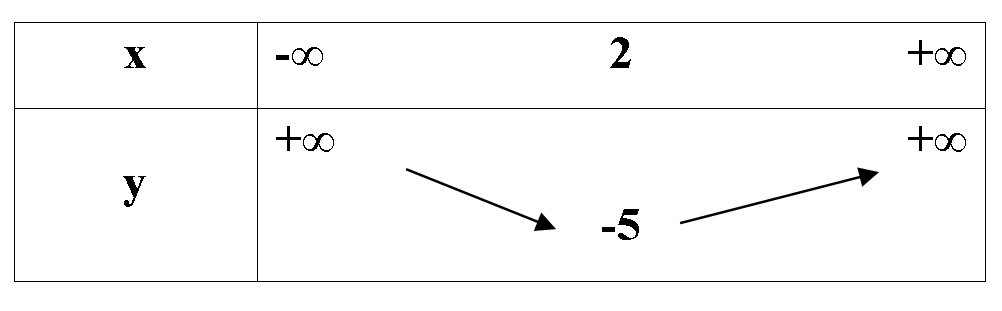
A. y=−x2+4x−9;
B. y=x2−4x−1;
C. y=−x2+4x;
D. y=x2−4x−5.
Hướng dẫn giải
Đáp án đúng là: B
Bảng biến thiên có bề lõm hướng lên nên a > 0. Do đó, loại đáp án A và C.
Đỉnh của parabol có tọa độ là (2; – 5). Xét các đáp án còn lại, ta có:
- Thay x = 2; y = – 5 vào phương trình y=x2−4x−1:
– 5 = 22 – 4.2 – 1 = – 5. Như vậy điểm (2; – 5) thuộc đồ thị của hàm số.
- Thay x = 2; y = – 5 vào phương trình y=x2−4x−5:
– 5 = 22 – 4.2 – 5 = – 9 (Vô lí). Như vậy (2; – 5) không thuộc đồ thị hàm số.