Lý thuyết Bất phương trình và hệ bất phương trình bậc nhất hai ẩn (Cánh diều 2024) Toán 10

Lý thuyết Toán lớp 10 Chương 2: Bất phương trình và hệ bất phương trình bậc nhất hai ẩn

Video giải Toán 10 Chương 2: Bất phương trình và hệ bất phương trình bậc nhất hai ẩn - Cánh diều

A. Lý thuyết Toán lớp 10 Chương 2: Bất phương trình và hệ bất phương trình bậc nhất hai ẩn

1. Bất phương trình bậc nhất hai ẩn

• Bất phương trình bậc nhất hai ẩn x, y là bất phương trình có một trong các dạng sau:

ax + by < c;          ax + by > c

ax + by ≤ c;           ax + by ≥ c

trong đó:    

x, y là các ẩn,

a, b, c là các số cho trước với a, b không đồng thời bằng 0.

• Cho bất phương trình bậc nhất hai ẩn ax + by < c (*).

Mỗi cặp số (x0; y0) sao cho ax0 + by0 < c gọi là một nghiệm của bất phương trình (*).

Trong mặt phẳng toạ độ Oxy, tập hợp các điểm có toạ độ là nghiệm của bất phương trình (*) được gọi là miền nghiệm của bất phương trình đó.

Nghiệm và miền nghiệm của các bất phương trình dạng ax + by > c; ax + by ≤ c và ax + by ≥ c được định nghĩa tương tự.

• Trong mặt phẳng toạ độ Oxy, đường thẳng d: ax + by = c chia mặt phẳng thành hai nửa mặt phẳng. Một trong hai nửa mặt phẳng (không kể d) là miền nghiệm của bất phương trình ax + by < c, nửa mặt phẳng còn lại (không kể d) là miền nghiệm của bất phương trình ax + by > c.

• Biểu diễn miền nghiệm của bất phương trình bậc nhất hai ẩn:

Bước 1. Vẽ đường thẳng d: ax + by = c. Đường thẳng d chia mặt phẳng toạ độ thành hai nửa mặt phẳng.

Bước 2. Lấy một điểm M(x0; y0) không nằm trên d (thường lấy gốc toạ độ O nếu c ≠ 0). Tính ax0 + by0 và so sánh với c.

Bước 3. Kết luận:

+ Nếu ax0 + by0 < c thì nửa mặt phẳng chứa điểm M (không kể d) là miền nghiệm của bất phương trình ax + by < c.

+ Nếu ax0 + by0 > c thì nửa mặt phẳng chứa điểm M (không kể d) là miền nghiệm của bất phương trình ax + by > c.

2. Hệ bất phương trình bậc nhất hai ẩn

• Hệ bất phương trình bậc nhất hai ẩn x, y là một hệ gồm một số bất phương trình bậc nhất hai ẩn x, y. Mỗi nghiệm chung của các bất phương trình trong hệ được gọi là một nghiệm của hệ bất phương trình đó.

• Miền nghiệm của hệ bất phương trình là giao của các miền nghiệm của các bất phương trình trong hệ.

• Biểu diễn miền nghiệm của hệ bất phương trình bậc nhất hai ẩn:

+ Trong cùng mặt phẳng toạ độ, biểu diễn miền nghiệm của mỗi bất phương trình trong hệ bằng cách gạch bỏ phần không thuộc miền nghiệm của nó.

+ Phần không bị gạch sau cùng là miền nghiệm cần tìm.

• Giá trị lớn nhất (hoặc nhỏ nhất) của biểu thức bậc nhất F(x , y) = ax + by trong miền đa giác A1A2…An là giá trị của F(x , y) tại một trong các đỉnh của đa giác đó.

B. Bài tập tự luyện

B.1 Bài tập tự luận

Bài 1. Một gia đình cần ít nhất 900 đơn vị protein và 400 đơn vị lipit trong thức ăn mỗi ngày. Mỗi kg thịt bò chừa 800 đơn vị protein và 200 đơn vị lipit. Mỗi kg thịt lợn chứa 600 đơn vị protein và 400 đơn vị lipit. Biết rằng gia đình này chỉ mua nhiều nhất 1,6 kg thịt bò và 1,1 kg thịt lợn, giá thịt bò là 250 nghìn/kg và thịt lợn là 160 nghìn/kg. Tính xem gia đình cần mua bao nhiêu kg mỗi loại thịt để chi phí là ít nhất.

Hướng dẫn giải:

Giả sử mỗi ngày gia đình này mua x kg thịt bò và y kg thịt lợn.

Điều kiện 0 ≤ x ≤ 1,6; 0 ≤ y ≤ 1,2.

Lượng protein và lipit trong thức ăn hàng ngày lần lượt là:

P = 800x + 600y ≥ 900 (đơn vị)

L = 200x + 400y ≥ 400 (đơn vị)

Từ đó, ta có hệ bất phương trình: $\left\{\begin{array}{l}0\le x\le 1,6\\ 0\le y\le 1,2\\ 8x+6y\ge 9\\ 2x+4y\ge 4\end{array}\right.$ 

Miền nghiệm của hệ bất phương trình được giới hạn bởi tứ giác ABCD, trong đó:

A(0,225 ; 1,2), B(1,6 ; 1,2), C(1,6 ; 0,2), D(0,6 ; 0,7).

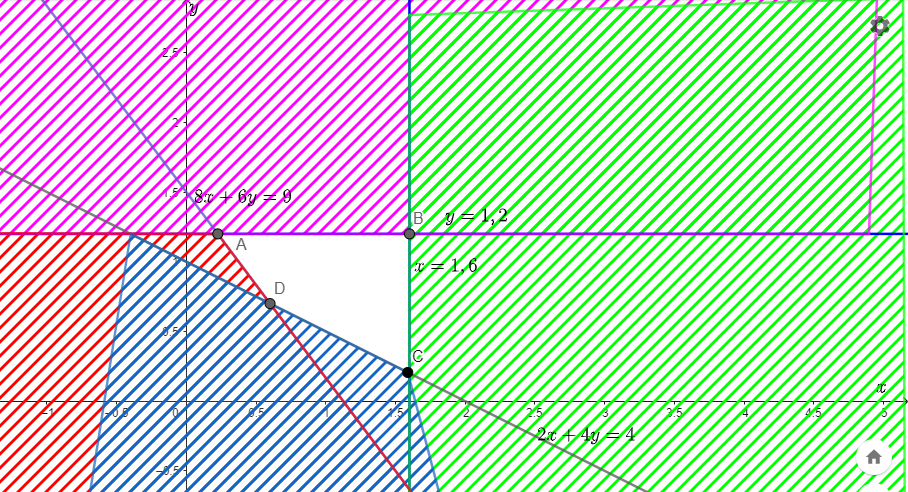
Số tiền mua thức ăn hàng ngày là:

T = 250x + 160y (nghìn đồng)

Xét giá trị của T tại các đỉnh của tứ giác ABCD, ta có:

Tại A(0,225 ; 1,2), với x = 0,225 và y = 1,2 thì T = 250.0,225 + 160.1,2 = 248,25;

Tại B(1,6 ; 1,2), với x = 1,6 và y = 1,2 thì T = 250.1,6 + 160.1,2 = 592;

Tại C(1,6 ; 0,2), với x = 1,6 và y = 0,2 thì T = 250.1,6 + 160.0,2 = 432;

Tại D(0,6 ; 0,7), với x = 0,6 và y = 0,7 thì T = 250.0,6 + 160.0,7 = 262.

Giá trị nhỏ nhất của T là 248,25 đạt được khi (x ; y) = (0,225; 1,2).

Vậy gia đình cần mua 0,025 kg thịt bò và 1,2 kg thịt lợn.

Bài 2. Biểu diễn miền nghiệm của mỗi bất phương trình sau:

a) $\frac{x}{3}+\frac{y}{2}<-1$                          

b) $x-\frac{3y}{2}\le 0$                           

c) $\frac{x+y}{2}\ge \frac{2x-y+1}{3}$ 

Hướng dẫn giải:

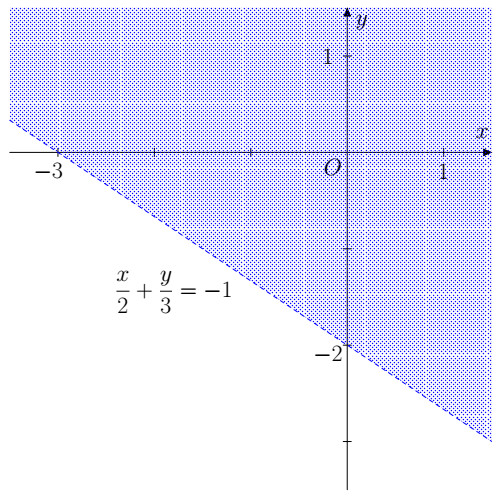
a) Dựng đường thẳng $\frac{x}{3}+\frac{y}{2}=-1$.

Thay giá trị (0 ; 0) vào bất phương trình, ta có $\frac{0}{2}+\frac{0}{3}=0<-1$ là mệnh đề sai.

Miền nghiệm là miền không chứa điểm (0 ; 0), không tính đường thẳng biên.

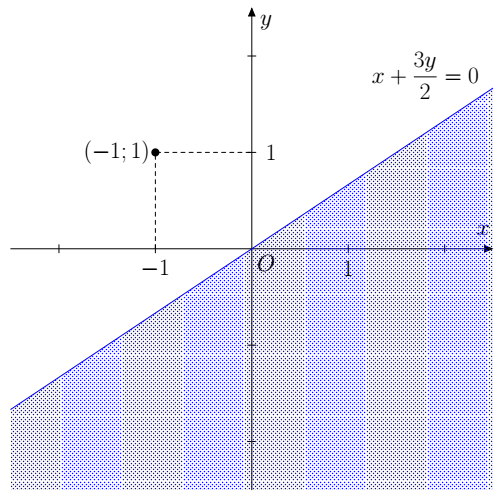
b) Dựng đường thẳng $x-\frac{3y}{2}=0$.

Lấy điểm (–1 ; 1) ta có: $-1-\frac{3.1}{2}=-\frac{5}{2}\le 0$ là mệnh đề đúng.

Miền nghiệm là miền chứa điểm (–1 ; 1) kể cả đường thẳng biên.

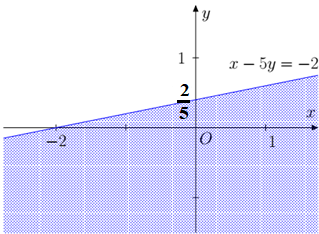
c) $\frac{x+y}{2}\ge \frac{2x-y+1}{3}$⇔3.(x + y) $\ge$ 2.(2x – y + 1) ⇔ x – 5y ≤ –2

Dựng đường thẳng x – 5y = –2.

Thay giá trị (0 ; 0) vào bất phương trình, ta có 0 – 0 = 0 ≤ –2 là mệnh đề sai.

Miền nghiệm là miền không chứa điểm (0 ; 0), kể cả đường thẳng biên.

Bài 3. Một gian hàng trưng bày bàn và ghế rộng 60m2. Diện tích để kê một chiếc ghế là 0,5m2, một chiếc bàn là 1,2m2. Gọi x là số ghế và y là số bàn được kê (x ≥ 0, y ≥ 0)

a) Viết bất phương trình bậc nhất hai ẩn x, y cho phần mặt sàn để kê bàn ghế.

b) Chỉ ra ba nghiệm của bất phương trình trên.

Hướng dẫn giải:

a) Diện tích kê x chiếc ghế và y chiếc bàn là 0,5x + 1,2y (m2).

Diện tích này không thể lớn hơn 60m2 nên ta được bất phương trình cần tìm:

0,5x + 1,2y ≤ 60 hay 5x + 12y ≤ 600.

b) Lấy ví dụ các cặp giá trị (10 ; 10), (30; 15), (24; 40), ta có:

5 . 10 + 12 . 10 = 170 ≤ 600 là mệnh đề đúng.

5 . 30 + 12 . 15 = 330 ≤ 600 là mệnh đề đúng.

5 . 24 + 12 . 40 = 600 ≤ 600 là mệnh đề đúng.

Vậy (10 ; 10), (30; 15), (24; 40) là ba nghiệm của bất phương trình 5x + 12y ≤ 600.

Bài 4. Biểu diễn trên hệ toạ độ miền nghiệm của hệ bất phương trình $\left\{\begin{array}{l}y+2x\le 8\\ x\le 4\\ x-2y\ge 3\\ x+y\ge 1\end{array}\right.$.

Từ đó tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức F(x , y) = –x – y với (x ; y) thoả mãn hệ bất phương trình trên.

Hướng dẫn giải:

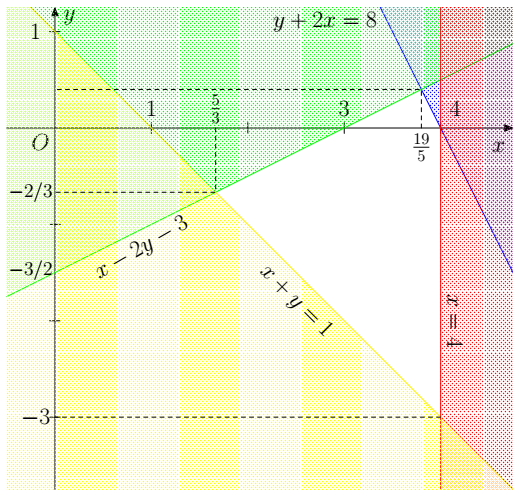
Dựng các đường thẳng y + 2x = 8, x = 4, x – 2y = 3, x + y = 1.

Do tọa độ điểm (3; 0) thỏa mãn các bất phương trình trong hệ nên miền nghiệm của từng bất phương trình trong hệ lần lượt là những nửa mặt phẳng không bị gạch chứa điểm (3; 0) không kể cả đường thẳng d1 và kể cả đường thẳng d2.

Miền nghiệm của hệ bất phương trình là miền tứ giác giới hạn bởi 4 điểm:

$\left(\frac{5}{3};-\frac{2}{3}\right)$; $\left(\frac{19}{5};\frac{2}{5}\right)$; (4 ; 0); (4 ; –3).

Lần lượt tính giá trị của F(x , y) tại các đỉnh của tứ giác, ta có:

$F\left(\frac{5}{3};-\frac{2}{3}\right)=-1$;    

$F\left(\frac{19}{5};\frac{2}{5}\right)=\frac{-21}{5}$;            

F(4 ; 0) = -4;         

F(4 ; -3) = -1

Vậy, giá trị lớn nhất của F là -1 đạt được tại $\left(\frac{5}{3};-\frac{2}{3}\right)$ và (4 ; -3); giá trị nhỏ nhất của F là $-\frac{21}{5}$ đạt được tại $\left(\frac{19}{5};\frac{2}{5}\right)$.

Bài 5. Biểu diễn miền nghiệm của các hệ bất phương trình sau:

a) $\left\{\begin{array}{l}x-2y>0\\ x+3y>-2\\ x-y\le 2\end{array}\right.$                                                     

b) $\left\{\begin{array}{l}y-2x>10\\ x>-5\\ y>5\\ x+y<5\end{array}\right.$ 

Hướng dẫn giải:

a) Dựng các đường thẳng x – y = 2; x – 2y = 0 và x + 3y = –2.

Điểm (1 ; 0) là nghiệm của cả ba bất phương trình x – 2y  > 0; x + 3y > –2 và x – y ≤ 2.

Miền nghiệm của hệ là miền không bị gạch trong hình dưới.

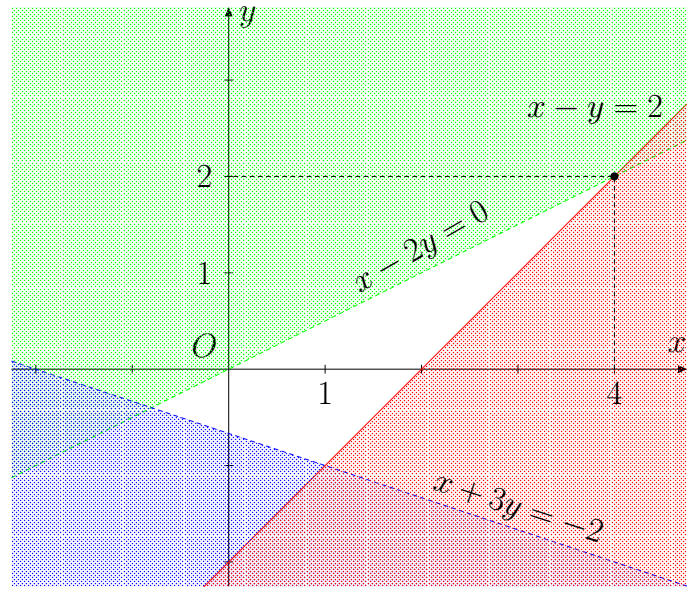
(Đường nét liền là miền nghiệm gồm cả biên, đường nét đứt là không gồm biên)

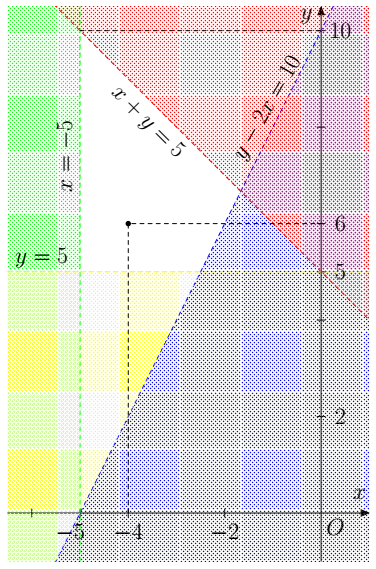
b) Dựng các đường thẳng y – 2x = 10; x = –5; y = 5 và x + y = 5.

Xét điểm (–4 ; 6) là nghiệm của cả bốn bất phương trình x – 2y > 10; x > –5; y > 5 và        x + y < 5.

Miền nghiệm của hệ là miền không bị gạch trong hình dưới.

Bài 6. Biểu diễn miền nghiệm của hệ bất phương trình:

$\left\{\begin{array}{l}\frac{x}{2}+\frac{y}{3}>0\\ \frac{x}{3}+\frac{y}{2}-1\le 0\\ x-\frac{3y}{2}<1\end{array}\right.$                                              

Hướng dẫn giải:

Ta có hệ bất phương trình được rút gọn: $\left\{\begin{array}{l}3x+2y>0\\ 2x+3y\le 6\\ 2x-3y<2\end{array}\right.$

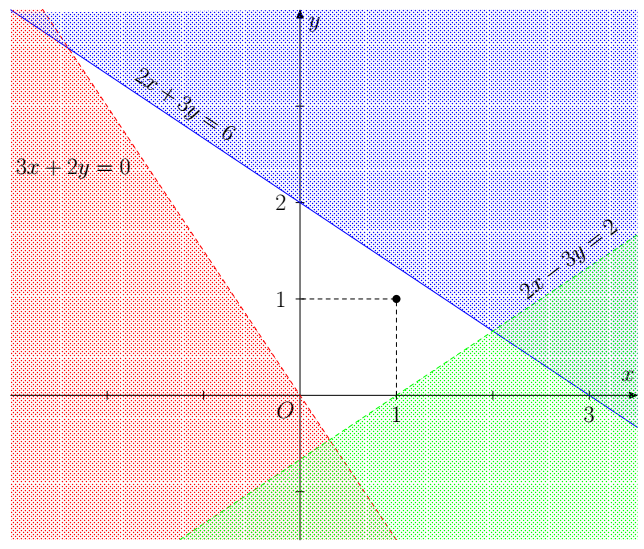
Dựng các đường thẳng:

d1: 3x + 2y = 0;

d2: 2x +3y = 6;

d3: 2x – 3y =2.

Do tọa độ điểm (1; 1) thỏa mãn các bất phương trình trong hệ nên miền nghiệm của từng bất phương trình trong hệ lần lượt là những nửa mặt phẳng không bị gạch chứa điểm (1; 1) không kể cả đường thẳng d1, d3 và kể cả đường thẳng d2.

Miền nghiệm của hệ là miền không bị gạch trong hình dưới.

Bài 7. Một hộ dân dự định dùng tối đa 8ha rừng để trồng cây keo và cây bạch đàn. Nếu trồng keo thì mỗi ha cần 20 công và thu về 300 triệu đồng, nếu trồng bạch đàn thì mỗi ha cần 30 công và thu về 400 triệu đồng. Hỏi cần trồng mỗi loại cây trên với diện tích là bao nhiêu để thủ được lãi cao nhất, với tổng số công không quá 180?

Hướng dẫn giải:

Gọi x (ha) là diện tích trồng keo, y (ha) là diện tích trồng bạch đàn.

Điều kiện x ≥ 0, y ≥ 0.

Tổng diện tích không quá 8 ha, tức là x + y ≤ 8 (ha).

Số công cần cho x ha keo là 20x (công)

Số công cần cho y ha bạch đàn là 30y (công)

Vì tổng số công không quá 180 nên ta có bất phương trình 20x + 30y ≤ 180 hay 2x + 3y ≤ 18.

Số tiền thu được là T = 300x + 400y (triệu đồng).

Ta cần tìm x, y thoả mãn hệ bất phương trình $\left\{\begin{array}{l}x\ge 0\\ y\ge 0\\ x+y\le 8\\ 2x+3y\le 18\end{array}\right.$ 

sao cho T = 300x + 400y đạt giá trị lớn nhất.

Miền nghiệm của hệ bất phương trình được biểu diễn bởi miền tứ giác OABC với O(0 ; 0), A(0 ; 6), B(6 ; 2), C(8 ; 0).

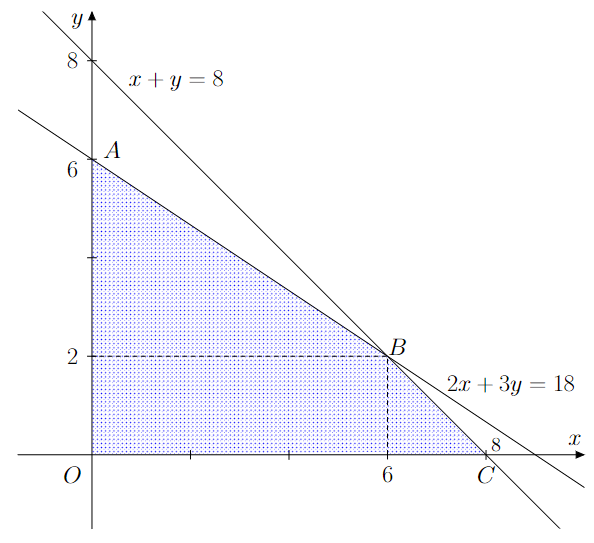
Xét giá trị của T tại các đỉnh của tứ giác, ta có:

Tại O(0 ; 0), với x = 0 và y = 0 thì T = 300.0 + 400.0 = 0;

Tại A(0 ; 6), với x = 0 và y = 6 thì T = 300.0 + 400.6 = 2 400;

Tại B(6 ; 2), với x = 6 và y = 2 thì T = 300.6 + 400.2 = 2 600;

Tại C(8 ; 0), với x = 8 và y = 0 thì T = 300.8 + 400.0 = 2 400.

Suy ra giá trị lớn nhất là T = 2 600 khi x = 6, y = 2 (toạ độ điểm B).

Vậy cần trồng 6 ha keo và 2 ha bạch đàn để thu được lợi nhuận lớn nhất.

B.2 Bài tập trắc nghiệm

Bài 1. Cho bất phương trình 2x + y > 3. Khẳng định nào sau đây là đúng:

A. Bất phương trình đã cho có nghiệm duy nhất;

B. Bất phương trình đã cho vô nghiệm;

C. Bất phương trình đã cho có vô số nghiệm;

D. Bất phương trình đã cho có tập nghiệm là [3 ; +∞).

Hướng dẫn giải:

Đáp án đúng là B

Bất phương trình bậc nhất hai ẩn 2x + y > 3 có vô số nghiệm, được biểu diễn bởi vô số điểm nằm trên nửa phẳng có biên là đường thẳng 2x + y = 3.

Câu 2. Phần không bị gạch trong hình vẽ nào trong các hình sau biểu diễn miền nghiệm của hệ bất phương trình $\left\{\begin{array}{c}x+y-2<0\\ 2x-y+2>0\end{array}\right.$.

A.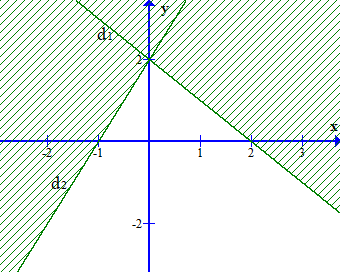 

B.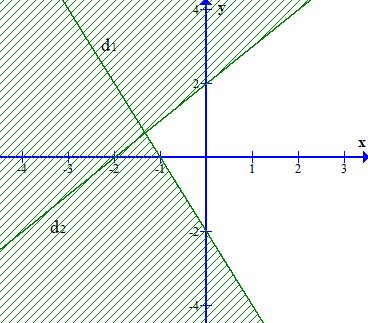 

C.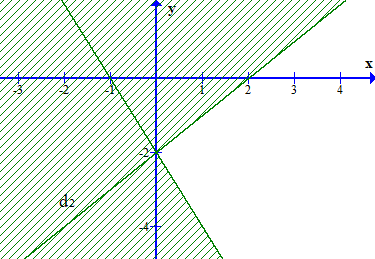 

D.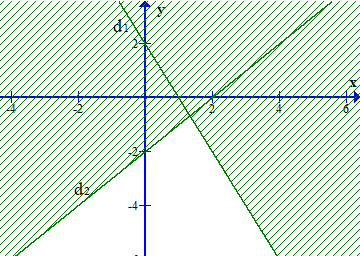 

Hướng dẫn giải

Đáp án đúng là: A

Vẽ đường thẳng d2: 2x – y + 2 = 0. Ta có đường thẳng đi qua hai điểm (0; 2) và (– 1; 0)

Xét điểm O(0; 0) thay vào phương trình đường thẳng ta có 2.0 – 0 + 2 > 0 thoả mãn bất phương trình 2x – y + 2 > 0. Vậy điểm O(0; 0) thuộc miền nghiệm của bất phương trình. Vậy miền nghiệm là phần nửa mặt phẳng được chia bởi đường thẳng d2 và chứa gốc toạ độ O(0; 0).

Vẽ đường thẳng d1: x + y – 2 = 0. Ta có đường thẳng đi qua hai điểm (0; 2) và (2; 0)

Xét điểm O(0; 0) thay vào phương trình đường thẳng ta có 0 + 0 – 2 < 0 thoả mãn bất phương trình x + y – 2 < 0. Vậy điểm O(0; 0) thuộc miền nghiệm của bất phương trình. Vậy miền nghiệm là phần nửa mặt phẳng được chia bởi đường thẳng d1 và chứa gốc toạ độ O(0; 0).

Vậy phần không bị gạch trong hình ở đáp án A biểu diễn miền nghiệm của hệ bất phương trình $\left\{\begin{array}{c}x+y-2<0\\ 2x-y+2>0\end{array}\right.$.

Câu 3. Cho bất phương trình 3x + 2 + 2(y – 2) < 2(x + 1) miền nghiệm của bất phương trình không chứa điểm nào sau đây?

A. (0; 0);

B. (1; 1);

C. (1; – 1);

D. (4; 2).

Hướng dẫn giải

Đáp án đúng là: D

3x + 2 + 2(y – 2) < 2(x + 1) ⇔ 3x + 2 + 2y – 4 < 2x + 2 ⇔ x + 2y – 4 < 0.

Xét đáp án A ta có: 0 + 2.0 – 4 < 0 thoả mãn bất phương trình x + 2y – 4 < 0, vậy điểm (0; 0) thuộc miền nghiệm.

Xét đáp án B ta có: 1 + 2.1 – 4 < 0 thoả mãn bất phương trình x + 2y – 4 < 0, vậy điểm (1; 1) thuộc miền nghiệm.

Xét đáp án C ta có: 0 + 2.( –1) – 4 < 0 thoả mãn bất phương trình x + 2y – 4 < 0, vậy điểm (1; – 1) thuộc miền nghiệm.

Xét đáp án D ta có: 4 + 2.2 – 4 > 0 không thoả mãn bất phương trình x + 2y – 4 < 0, vậy điểm (4; 2) không thuộc miền nghiệm.

Câu 4. Phần không bị gạch trong hình vẽ nào trong các hình sau biểu diễn miền nghiệm của hệ bất phương trình $\left\{\begin{array}{l}x-2y<1\\ 2x-y+2>0\end{array}\right.$.

A.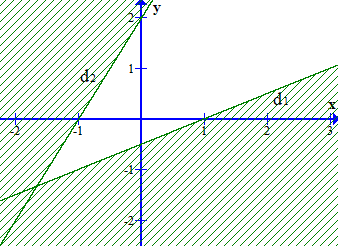 

B.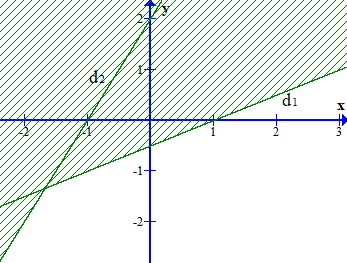 

C.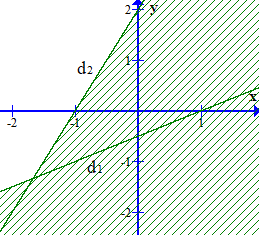 

D.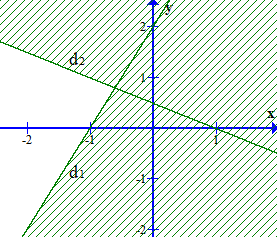 

Hướng dẫn giải

Đáp án đúng là: A

Vẽ đường thẳng d1 : x – 2y = 1, đường thẳng đi qua hai điểm $\left(0;-\frac{1}{2}\right)$ và (1; 0).

Xét điểm O(0; 0) thay vào phương trình đường thẳng ta có 0 – 2.0 = 0 < 1 thoả mãn bất phương trình x – 2y < 1. Vậy điểm O(0; 0) thuộc miền nghiệm của bất phương trình. Miền nghiệm là nửa mặt phẳng được chia bởi đường thẳng d1 và chứa gốc toạ độ O(0; 0).

Vẽ đường thẳng d2: 2x – y + 2 = 0, đường thẳng đi qua hai điểm (0; 2) và (– 1; 0)

Xét điểm O(0; 0) thay vào phương trình đường thẳng ta có 2.0 – 0 + 2 > 0 thoả mãn bất phương trình 2x – y + 2 > 0. Vậy điểm O(0; 0) thuộc miền nghiệm của bất phương trình. Vậy miền nghiệm là phần nửa mặt phẳng được chia bởi đường thẳng d2 và chứa gốc toạ độ O(0; 0).

Vậy phần không bị gạch trong hình ở đáp án A biểu diễn miền nghiệm của hệ bất phương trình $\left\{\begin{array}{l}x-2y<1\\ 2x-y+2>0\end{array}\right.$.

Câu 5. Cặp số nào sau đây không là nghiệm của bất phương trình 5x – 2(y – 1) ≤ 0?

A. (0; 1) ;

B. (1 ; 3);

C. (– 1; 1);

D. (– 1; 0).

Hướng dẫn giải

Đáp án đúng là: B

Ta có 5x – 2(y – 1) ≤ 0 ⇔ 5x – 2y + 2 ≤ 0.

Xét đáp án A: Thay cặp số (0; 1) vào bất phương trình ta có 5.0 – 2.1 + 2 = 0 thoả mãn bất phương trình 5x – 2y + 2 ≤ 0. Cặp số (0; 1) là nghiệm của bất phương trình. Đáp án A sai.

Xét đáp án B: Thay cặp số (1; 3) vào bất phương trình ta có 5.1 – 2.3 + 2 = 1 không thoả mãn bất phương trình 5x – 2y + 2 ≤ 0. Cặp số (1; 3) không là nghiệm của bất phương trình. Đáp án B đúng.

Xét đáp án C: Thay cặp số (– 1; 1) vào bất phương trình ta có 5.( – 1) – 2.1 + 2 = – 5 thoả mãn bất phương trình 5x – 2y + 2 ≤ 0. Cặp số (– 1; 1) là nghiệm của bất phương trình. Đáp án C sai.

Xét đáp án D: Thay cặp số (– 1; 0) vào bất phương trình ta có 5.( – 1) – 2.0 + 2 = – 3 thoả mãn bất phương trình 5x – 2y + 2 ≤ 0. Cặp số (– 1; 0) là nghiệm của bất phương trình. Đáp án D sai.