Lý thuyết Tổng và hiệu của hai vectơ (Chân trời sáng tạo 2024) Toán 10

Tóm tắt lý thuyết Toán 10 Bài 2: Tổng và hiệu của hai vectơ ngắn gọn, chính xác sách Chân trời sáng tạo sẽ giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt Toán 10.

1 77 lượt xem

Bài trước

Bài sau

Nội dung bài viết

A. Lý thuyết Tổng và hiệu của hai vectơ

1. Tổng của hai vectơ

2. Tính chất của phép cộng các vectơ

3. Hiệu của hai vectơ

4. Tính chất vectơ của trung điểm đoạn thẳng và trọng tâm tam giác

B. Bài tập tự luyện

Lý thuyết Toán lớp 10 Bài 2: Tổng và hiệu của hai vectơ

A. Lý thuyết Tổng và hiệu của hai vectơ

1. Tổng của hai vectơ

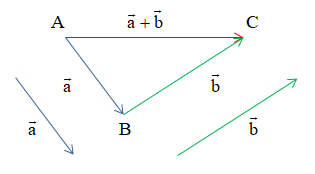
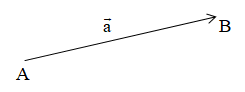
Cho hai vectơ $\vec{a}$ và $\vec{b}$ . Từ một điểm A tùy ý, lấy hai điểm B, C sao cho $\vec{A B} = \vec{a}, \vec{B C} = \vec{b}$ . Khi đó $\vec{A C}$ được gọi là tổng của hai vectơ $\vec{a}$ và $\vec{b}$ và được kí hiệu là $\vec{a} + \vec{b}$ .

Vậy $\vec{a} + \vec{b} = \vec{A B} + \vec{B C} = \vec{A C}$ .

Phép toán tìm tổng của hai vectơ được gọi là phép cộng vectơ.

Quy tắc ba điểm

Với ba điểm M, N, P, ta có $\vec{M N} + \vec{N P} = \vec{M P}$ .

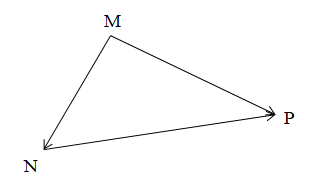
Chú ý: Khi cộng vectơ theo quy tắc ba điểm, điểm cuối của vectơ thứ nhất phải là điểm đầu của vectơ thứ hai.

Ví dụ: Cho các điểm A, B, C, D, E, F phân biệt. Thực hiện phép cộng các vectơ:

$\vec{A C} + \vec{C D}; \vec{B C} + \vec{C B}; \vec{D C} + \vec{C E} + \vec{E F}$ .

Hướng dẫn giải

Áp dụng quy tắc ba điểm, ta có:

$\vec{A C} + \vec{C D} = \vec{A D}$ .

$\vec{B C} + \vec{C B} = \vec{B B} = \vec{0}$ .

$\vec{D C} + \vec{C E} + \vec{E F} = \vec{D E} + \vec{E F} = \vec{D F}$ .

Quy tắc hình bình hành

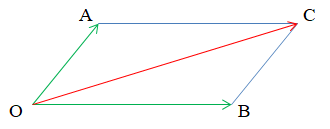
Nếu OACB là hình bình hành thì ta có $\vec{O A} + \vec{O B} = \vec{O C}$ .

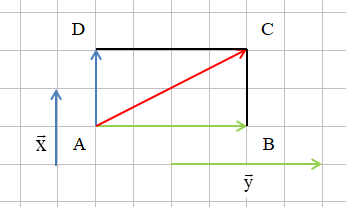
Ví dụ: Cho hình chữ nhật MNPQ và hai vectơ $\vec{x}, \vec{y}$ như hình bên. Tính tổng của hai vectơ $\vec{x}$ và $\vec{y}$ .

Hướng dẫn giải

Ta có $\vec{x} = \vec{A D}, \vec{y} = \vec{A B}$ .

Suy ra $\vec{x} + \vec{y} = \vec{A D} + \vec{A B}$ .

Theo quy tắc hình bình hành, ta có $\vec{A D} + \vec{A B} = \vec{A C}$ .

Vậy $\vec{x} + \vec{y} = \vec{A C}$ .

2. Tính chất của phép cộng các vectơ

Phép cộng vectơ có các tính chất sau:

+ Tính chất giao hoán: $\vec{a} + \vec{b} = \vec{b} + \vec{a}$ .

+ Tính chất kết hợp: $(\vec{a} + \vec{b}) + \vec{c} = \vec{a} + (\vec{b} + \vec{c})$ .

+ Với mọi $\vec{a}$ , ta luôn có: $\vec{a} + \vec{0} = \vec{0} + \vec{a} = \vec{a}$ .

Chú ý: Từ tính chất kết hợp, ta có thể xác định được tổng của ba vectơ $\vec{a}, \vec{b}, \vec{c}$ ,kí hiệu là $\vec{a} + \vec{b} + \vec{c}$ với $\vec{a} + \vec{b} + \vec{c} = (\vec{a} + \vec{b}) + \vec{c}$ .

Ví dụ: Cho tứ giác MNPQ. Thực hiện các phép cộng vectơ sau:

a) $(\vec{M N} + \vec{P M}) + \vec{N Q}$ .

b) $\vec{M N} + \vec{Q P} + \vec{N Q} + \vec{P M}$ .

Hướng dẫn giải

Áp dụng tính chất giao hoán và tính chất kết hợp của phép cộng vectơ, ta được:

a) $(\vec{M N} + \vec{P M}) + \vec{N Q} = (\vec{P M} + \vec{M N}) + \vec{N Q} = \vec{P N} + \vec{N Q} = \vec{P Q}$ .

b) $\vec{M N} + \vec{Q P} + \vec{N Q} + \vec{P M} = (\vec{M N} + \vec{N Q}) + (\vec{Q P} + \vec{P M}) = \vec{M Q} + \vec{Q M} = \vec{M M} = \vec{0}$ .

Chú ý: Cho vectơ tùy ý $\vec{a} = \vec{A B}$ .

Ta có $\vec{a} + (- \vec{a}) = \vec{A B} + (- \vec{A B}) = \vec{A B} + \vec{B A} = \vec{A A} = \vec{0}$ .

Tổng hai vectơ đối nhau luôn bằng vectơ-không: $\vec{a} + (- \vec{a}) = \vec{0}$ .

3. Hiệu của hai vectơ

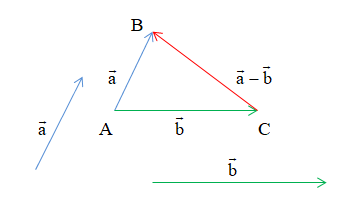
Cho hai vectơ $\vec{a}$ và $\vec{b}$ . Hiệu của hai vectơ $\vec{a}$ và $\vec{b}$ là vectơ \ $\vec{a} + (- \vec{b})$ và kí hiệu là $\vec{a} - \vec{b}$ .

Phép toán tìm hiệu của hai vectơ được gọi là phép trừ vectơ.

Ví dụ: Cho các điểm D, E, F, G phân biệt. Thực hiện các phép trừ vectơ sau: $\vec{D E} - \vec{F E}; \vec{G D} - \vec{G F}$ .

Hướng dẫn giải

Ta có: $\vec{D E} - \vec{F E} = \vec{D E} + (- \vec{F E}) = \vec{D E} + \vec{E F} = \vec{D F}$ .

$\vec{G D} - \vec{G F} = \vec{G D} + (- \vec{G F}) = \vec{G D} + \vec{F G} = \vec{F G} + \vec{G D} = \vec{F D}$ .

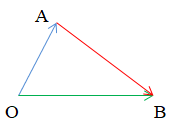
Chú ý: Cho ba điểm O, A, B, ta có: $\vec{O B} - \vec{O A} = \vec{A B}$ .

Ví dụ: Cho hình vuông ABCD và một điểm M tùy ý. Thực hiện các phép trừ vectơ sau: $\vec{O B} - \vec{O D}; (\vec{O C} - \vec{O A}) + (\vec{D B} - \vec{D C})$ .

Hướng dẫn giải

Ta có $\vec{O B} - \vec{O D} = \vec{D B}$ .

$(\vec{O C} - \vec{O A}) + (\vec{D B} - \vec{D C}) = \vec{A C} + \vec{C B} = \vec{A B}$ .

4. Tính chất vectơ của trung điểm đoạn thẳng và trọng tâm tam giác

Điểm M là trung điểm của đoạn thẳng AB khi và chỉ khi $\vec{M A} + \vec{M B} = \vec{0}$ .

Điểm G là trọng tâm của tam giác ABC khi và chỉ khi $\vec{G A} + \vec{G B} + \vec{G C} = \vec{0}$ .

Ví dụ: Cho hình bình hành ABCD có tâm O. Hai điểm E, F lần lượt là trung điểm AB, BC. Gọi G là trọng tâm của tam giác ABC. Chứng minh rằng:

a) $\vec{O A} + \vec{O C} + \vec{O D} + \vec{O E} + \vec{O F} = \vec{0}$ .

b) $\vec{G A} + \vec{G C} + \vec{G D} = \vec{B D}$ .

Hướng dẫn giải

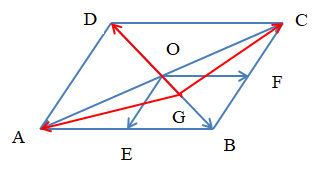
a) Vì ABCD là hình bình hành tâm O nên O là trung điểm AC (tính chất hình bình hành).

Lại có E là trung điểm AB (gt)

Do đó OE là đường trung bình của tam giác ABC.

Suy ra OE // BC và OE = $\frac{1}{2} B C$ = BF (với F là trung điểm BC).

Khi đó ta có tứ giác OEBF là hình bình hành.

Áp dụng quy tắc hình bình hành cho OEBF, ta được: $\vec{O E} + \vec{O F} = \vec{O B}$ .

Vì ABCD là hình bình hành tâm O nên O là trung điểm AC và BD (tính chất hình bình hành).

Do đó $\vec{O A} + \vec{O C} = \vec{0}$ và $\vec{O D} + \vec{O B} = \vec{0}$ .

Ta có $\vec{O A} + \vec{O C} + \vec{O D} + \vec{O E} + \vec{O F}$

$= (\vec{O A} + \vec{O C}) + \vec{O D} + (\vec{O E} + \vec{O F})$

$= \vec{0} + \vec{O D} + \vec{O B} = \vec{0} + \vec{0} = \vec{0}$ .

Vậy $\vec{O A} + \vec{O C} + \vec{O D} + \vec{O E} + \vec{O F} = \vec{0}$ .

b) Vì G là trọng tâm của tam giác ABC nên $\vec{G A} + \vec{G B} + \vec{G C} = \vec{0}$ .

Theo quy tắc ba điểm, ta có: $\vec{G D} = \vec{G B} + \vec{B D} = \vec{G B} + \vec{B C} + \vec{C D}$ .

Ta có $\vec{G A} + \vec{G C} + \vec{G D}$

$= \vec{G A} + \vec{G C} + \vec{G B} + \vec{B C} + \vec{C D}$

$= (\vec{G A} + \vec{G C} + \vec{G B}) + (\vec{B C} + \vec{C D})$

$= \vec{0} + \vec{B D} = \vec{B D}$ .

Vậy $\vec{G A} + \vec{G C} + \vec{G D} = \vec{B D}$ .

B. Bài tập tự luyện

Bài 1. Cho hình vuông ABCD cạnh a, tâm O. Tính độ dài các vectơ:

a) $\vec{A B} + \vec{A D}$ .

b) $\vec{O A} - \vec{C B}$ .

Hướng dẫn giải

a) Vì ABCD là hình vuông nên $\vec{A B} + \vec{A D} = \vec{A C}$ .

Do đó $|\vec{A B} + \vec{A D}| = |\vec{A C}| = A C$ .

Tam giác ABC vuông tại B: AC2 = AB2 + BC2 (Định lý Py ‒ ta ‒ go)

⇔ AC2 = a2 + a2 = 2a2

⇒ AC = $a \sqrt{2}$ .

Vậy $|\vec{A B} + \vec{A D}| = a \sqrt{2}$ .

b) Vì ABCD là hình vuông nên ta có BD = AC = $a \sqrt{2}$ và AD = CB.

Mà $\vec{C B}, \vec{A D}$ ngược hướng.

Do đó $\vec{A D} = - \vec{C B}$ .

Ta có $\vec{O A} - \vec{C B} = \vec{O A} + \vec{A D} = \vec{O D}$ .

Do đó $|\vec{O A} - \vec{C B}| = |\vec{O D}| = O D$ .

Vì O là tâm của hình vuông ABCD nên O là trung điểm BD.

Do đó OD = $\frac{B D}{2} = \frac{a \sqrt{2}}{2}$ .

Vậy $|\vec{O A} - \vec{C B}| = \frac{a \sqrt{2}}{2}$ .

Bài 2. Cho hình bình hành ABCD có O là giao điểm của hai đường chéo. Chứng minh rằng:

a) $\vec{O A} + \vec{O B} + \vec{O C} + \vec{O D} = \vec{0}$ .

b) $\vec{D A} - \vec{D B} + \vec{D C} = \vec{0}$ .

c) $\vec{D O} + \vec{A O} = \vec{A B}$ .

Hướng dẫn giải

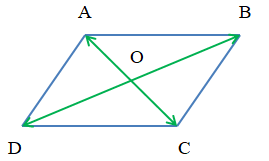
a) Vì O là tâm của hình bình hành ABCD nên O là trung điểm của AC và BD (tính chất hình bình hành).

Do đó ta có $\vec{O A} + \vec{O C} = \vec{0}$ (1) và $\vec{O B} + \vec{O D} = \vec{0}$ (2).

Lấy (1) + (2) vế theo vế ta được: $\vec{O A} + \vec{O B} + \vec{O C} + \vec{O D} = \vec{0} + \vec{0} = \vec{0}$ .

b) Vì ABCD là hình bình hành nên BA // DC và BA = DC.

Mà $\vec{B A}, \vec{D C}$ ngược hướng.

Do đó $\vec{B A} = - \vec{D C}$ .

Ta suy ra $\vec{B A} + \vec{D C} = \vec{0}$ .

Ta có $\vec{D A} - \vec{D B} + \vec{D C} = \vec{B A} + \vec{D C} = \vec{0}$ .

c) Ta có O là trung điểm BD nên DO = OB.

Mà $\vec{D O}, \vec{O B}$ cùng hướng.

Do đó $\vec{D O} = \vec{O B}$ .

Ta có $\vec{D O} + \vec{A O} = \vec{O B} + \vec{A O} = \vec{A O} + \vec{O B} = \vec{A B}$ .

Bài 3. Một con thuyền trôi theo hướng nam vận tốc 25 km/h, dòng nước chảy theo hướng đông với vận tốc 10 km/h. Tính độ dài vectơ tổng của hai vectơ nói trên (làm tròn kết quả đến hàng trăm).

Hướng dẫn giải

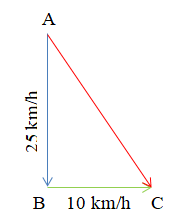
Gọi A là vị trí con thuyền xuất phát.

Vận tốc của con thuyền được biểu diễn bởi $\vec{A B}$ .

Vận tốc của dòng nước được biểu diễn bởi $\vec{B C}$ .

Khi đó ta có vectơ tổng của hai vectơ nói trên là $\vec{A B} + \vec{B C} = \vec{A C}$ .

Do đó độ lớn của vectơ cần tìm là: $|\vec{A B} + \vec{B C}| = |\vec{A C}| = A C$ .

Vì con thuyền trôi theo hướng nam và dòng nước chảy theo hướng đông.

Nên ta có AB ⊥ BC.

Ta có độ lớn vận tốc con thuyền là 25 km/h.

Suy ra $|\vec{A B}|$ = AB = 25.

Ta có độ lớn vận tốc dòng nước là 10 km/h.

Suy ra $|\vec{B C}|$ = BC = 10.

Tam giác ABC vuông tại B: AC2 = AB2 + BC2 (Định lý Py ‒ ta ‒ go)

⇔ AC2 = 252 + 102 = 725.

⇒ AC = $5 \sqrt{29}$ ≈ 26,93.

Vậy độ dài vectơ tổng của hai vectơ nói đến trong bài xấp xỉ bằng 26,93 (km/h).

1 77 lượt xem

Bài trước

Bài sau

Lý thuyết Tổng và hiệu của hai vectơ (Chân trời sáng tạo 2024) Toán 10