Lý thuyết Xác suất của biến cố (Chân trời sáng tạo 2024) Toán 10

Lý thuyết Toán lớp 10 Bài 2: Xác suất của biến cố

A. Lý thuyết Xác suất của biến cố

1. Xác suất của biến cố

– Giả sử một phép thử có không gian mẫu Ω gồm hữu hạn các kết quả có cùng khả năng xảy ra và A là một biến cố.

Xác suất của biến cố A là một số, kí hiệu là P(A), được xác định bởi công thức:

P(A) = $\frac{n\left(A\right)}{n\left(\Omega \right)}$   

Trong đó n(A) và n($\Omega$) lần lượt là kí hiệu số phần tử của tập A và $\Omega$ .

Chú ý:

+ Định nghĩa trên được gọi là định nghĩa cổ điển của xác suất.

+ Với mọi biến cố A, 0 ≤ P(A) ≤ 1.

+ P($\Omega$) = 1, P(∅) = 0.

+ Xác suất của mỗi biến cố đo lường xảy ra của biến cố đó. Biến cố có khả năng xảy ra càng cao thì xác suất của nó càng gần 1.

Ví dụ: Trong hộp có 3 viên bi xanh và 5 viên bi đỏ. Lấy ngẫu nhiên trong hộp 3 viên bi. Tính xác suất của biến cố A: “Lấy ra được 3 viên bi màu đỏ”.

Hướng dẫn giải

– Tính số phần tử của không gian mẫu:

Lấy 3 viên bi ngẫu nhiên trong 8 viên bi có $C_8^3$  cách.

Do đó số phần tử của không gian mẫu là n($\Omega$) = $C_8^3$ = 56.

– Tính số kết quả thuận lợi cho biến cố A:

Lấy được 3 viên bi màu đỏ trong số 5 viên bi màu đỏ có $C_5^3$  cách.

Do đó, số kết quả thuận lợi cho biến cố A là n(A) = $C_5^3$  = 10.

Xác suất của biến cố A: “Lấy ra được 3 viên bi màu đỏ” là:

P(A) = $\frac{n\left(A\right)}{n\left(\Omega \right)}$  =$\frac{10}{56}=\frac{5}{28}$

Vậy xác suất của biến cố A là P(A) = $\frac{5}{28}$ .

2. Tính xác suất bằng sơ đồ hình cây

– Trong chương VIII, chúng ta đã được làm quen với phương pháp sử dụng sơ đồ hình cây để liệt kê các kết quả của một thí nghiệm. Ta cũng có thể sử dụng sơ đồ hình cây để tính xác suất

Ví dụ: Tung một đồng xu cân đối và đồng chất 3 lần liên tiếp. Tính xác suất của biến cố A: “Trong 3 lần tung có ít nhất 1 lần xuất hiện mặt ngửa”.

Hướng dẫn giải

Kí hiệu S nếu tung được mặt sấp, N nếu tung được mặt ngửa.

Các kết quả có thể xảy ra trong 3 lần tung được thể hiện trong sơ đồ hình cây dưới đây:

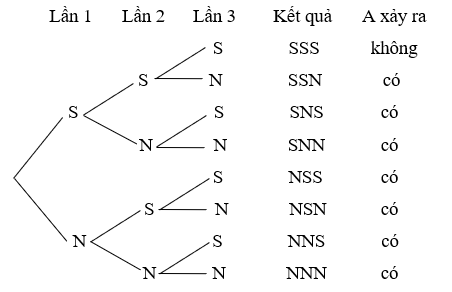
Có tất cả 8 kết quả xảy ra, trong đó có 7 kết quả thuận lợi cho biến cố A.

Do đó:

P(A) = $\frac{7}{8}$ .

3. Biến cố đối

– Cho A là một biến cố. Khi đó biến cố “Không xảy ra A”, kí hiệu là $\left(\overline{A}\right)$ , được gọi là biến cố đối của A.

$\overline{A}=\Omega \backslash A$; P$\left(\overline{A}\right)$  + P(A) = 1.

Ví dụ: Trong giỏ có 3 quả cam, 4 quả táo và 2 quả đào. Lấy ngẫu nhiên từ trong giỏ ra 4 quả. Tính xác suất để trong 4 quả lấy ra có ít nhất 1 quả táo.

Hướng dẫn giải

Gọi A là biến cố “Trong 4 quả lấy ra có ít nhất 1 quả táo”.

Thì biến cố đối của A là $\overline{A}$ : “Trong 4 quả lấy ra không có quả táo nào”.

Ta sẽ tính xác suất của biến cố $\overline{A}$ :

Lấy 4 quả trong tổng số 3 + 4 + 2 = 9 quả có  cách.

Do đó, số phần tử của không gian mẫu là n$\left(\Omega \right)$= $C_9^4$  = 126.

Lấy 4 quả trong số 5 quả cam và đào thì có $C_5^4$cách.

Do đó, số kết quả thuận lợi cho biến cố $\overline{A}$ là: n($\overline{A}$) = $C_5^4$ = 5.

Xác suất của biến cố $\overline{A}$  là: P$\left(\overline{A}\right)$ =$\frac{n\left(\overline{A}\right)}{n\left(\Omega \right)}=\frac{5}{126}$

Suy ra xác suất của biến cố A là:

P(A) = 1 – P$\left(\overline{A}\right)$ =$\frac{121}{126}$.

4. Nguyên lí xác suất bé

Trong thực tế, các biến cố có xác suất xảy ra gần bằng 1 thì gần như là luôn xảy ra trong một phép thử. Ngược lại, các biến cố mà xác suất xảy ra gần bằng 0 thi gần như không xảy ra trong một phép thử.

Trong Lí thuyết Xác suất, Nguyên lí xác suất bé được phát biểu như sau:

Nếu một biến cố có xác suất rất bé thì trong một phép thử, biến cố đó sẽ không xảy ra.

Ví dụ: Khi một con tàu lưu thông trên biển, xác suất nó bị đắm là số dương. Tuy nhiên, nếu tuân thủ các quy tắc an toàn thi xác suất xảy ra biển cố này là rất nhỏ, con tàu có thể yên tâm hoạt động.

Nếu một nhà sản xuất tuyên bố tỉ lệ gây sốc phản vệ nặng khi tiêm một loại vắc xin là rất nhỏ, chỉ khoảng 0,001, thì có thể tiêm vắc xin đó cho mọi người được không? Câu trả lời là không, vì sức khoẻ và tính mạng con người là vô giá, nếu tiêm loại vắc xin đó cho hàng tỉ người thì khả năng có nhiều người bị sốc phản vệ nặng là rất cao.

B. Bài tập tự luyện

Bài 1. Chọn ngẫu nhiên ba số tự nhiên trong các số tự nhiên từ 1 đến 50. Tính xác suất của biến cố B: “Trong ba số có một số là số chính phương, hai số còn lại chia hết cho 5”.

Hướng dẫn giải

Từ 1 đến 50 có 50 số tự nhiên.

Chọn ngẫu nhiên 3 số tự nhiên trong 50 số ta có $C_{50}^3$  cách.

Do đó số phần tử của không gian mẫu là: n$\left(\Omega \right)$= $C_{50}^3$  = 19 600.

Từ 1 đến 50 có các số chính phương là: 1, 4, 9, 16, 25, 36, 49 (7 số).

Từ 1 đến 50 có các số chia hết cho 5 là: 5; 10; 15; 20; 25; 30; 35; 40; 45; 50 (10 số).

Chọn 1 số trong 7 số chính phương có $C_7^1$  cách.

Chọn 2 số trong 10 số chính phương có $C_{10}^2$  cách.

Theo quy tắc nhân, số kết quả thuận lợi cho biến cố B là:

n(B) = $C_7^1$ .$C_{10}^2$  = 315.

Xác suất của biến cố B là: P(B) = $\frac{n\left(B\right)}{n\left(\Omega \right)}=\frac{315}{19600}=\frac{9}{560}$ .

Vậy xác suất của biến cố B: “Trong ba số có một số là số chính phương, hai số còn lại chia hết cho 5” là

Bài 2. Trong một chiếc hộp có 20 viên bi, trong đó có 8 viên bi màu đỏ, 7 viên bi màu xanh và 5 viên bi màu vàng. Lấy ngẫu nhiên ra 3 viên bi. Tính xác suất để 3 viên bi lấy ra đều màu đỏ.

Hướng dẫn giải

Gọi biến cố A: “3 viên bi lấy ra đều màu đỏ”.

Số cách lấy 3 viên bi từ 20 viên bi là: $C_{20}^3$ .

Do đó số phần tử của không gian mẫu là: n$\left(\Omega \right)$= $C_{20}^3$ = 1140.

Lấy 3 viên bi màu đỏ từ 8 viên bi đỏ là: $C_8^3$.

Số kết quả thuận lợi cho biến cố A là: n(A) = $C_8^3$ = 56.

Xác suất của biến cố A: “3 viên bi lấy ra đều màu đỏ” là:

P(A) =$\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{56}{1140}=\frac{14}{285}$ .

Vậy xác suất để 3 viên bi lấy ra đều màu đỏ là $\frac{14}{285}.$

Bài 3. Bạn Nam có 3 chiếc ảnh giấy. Nam tung lần lượt từng chiếc ảnh lên để rơi trên bàn. Tính xác suất để sau 3 lần tung thì 3 chiếc ảnh có 2 chiếc sấp, 1 chiếc ngửa. (Tính theo phương pháp sơ đồ hình cây).

Hướng dẫn giải

Gọi A là biến cố “Sau 3 lần tung thì 3 chiếc ảnh có 2 chiếc sấp, 1 chiếc ngửa”.

Kí hiệu S nếu Nam tung được mặt sấp, N nếu Nam tung được mặt ngửa.

Các kết quả có thể xảy ra trong 3 lần tung được thể hiện trong sơ đồ hình cây dưới đây:

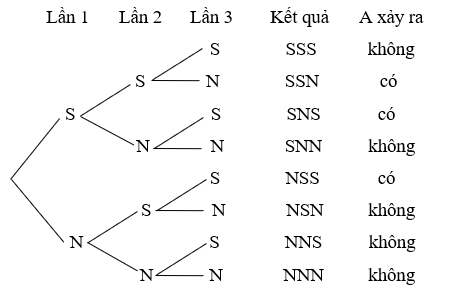
Có tất cả 8 kết quả xảy ra, trong đó có 3 kết quả thuận lợi cho biến cố A.

Do đó: P(A) =$\frac{3}{8}$  

Vậy xác suất để sau 3 lần tung thì 3 chiếc ảnh có 2 chiếc sấp, 1 chiếc ngửa là $\frac{3}{8}$

Bài 4. Ngân hàng đề thi môn Toán gồm 100 câu hỏi chỉ nằm trong 2 chương I và II. Thầy giáo chọn 10 câu hỏi để ra đề. Tính xác suất để thầy giáo chọn ít nhất 1 câu trong chương I, biết số câu hỏi của chương I gấp 3 lần số câu hỏi chương II.

Hướng dẫn giải

Số câu hỏi của chương I gấp 3 lần số câu hỏi chương II mà tổng số câu hỏi của 2 chương là 100 nên số câu hỏi của chương I là 75 câu và số câu hỏi của chương II là 25 câu.

Thầy giáo chọn 10 câu hỏi trong 100 câu hỏi có $C_{100}^{10}$ cách.

Do đó số phần tử của không gian mẫu là n$\left(\Omega \right)$=$C_{100}^{10}$ .

Gọi A là biến cố: “Thầy giáo chọn ít nhất 1 câu trong chương I”.

Suy ra biến cố $\overline{A}$ là: “Thầy giáo không chọn câu nào trong chương I”.

Chọn 10 câu hỏi trong 25 câu hỏi của chương II có $C_{25}^{10}$  cách.

Do đó sối kết quả thuận lợi cho biến cố $\overline{A}$  là: n$\left(\overline{A}\right)$= $C_{25}^{10}$ .

Xác suất của biến cố $\overline{A}$  là: P$\left(\overline{A}\right)$=$\frac{n\left(\overline{A}\right)}{n\left(\Omega \right)}=\frac{C_{25}^{10}}{C_{100}^{10}}$  

Xác suất của biến cố A là:

P(A) = 1 – P$\left(\overline{A}\right)$ = 1 – $\frac{C_{25}^{10}}{C_{100}^{10}}$  ≈ 0,9999998112.

Vậy xác suất để thầy giáo chọn ít nhất 1 câu trong chương I là khoảng 0,9999998112.