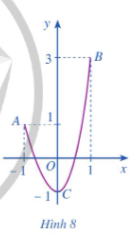
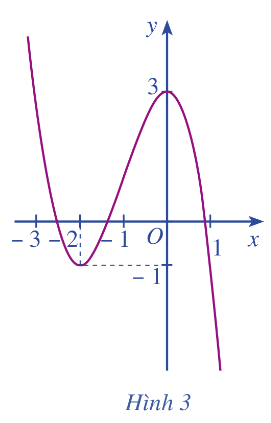
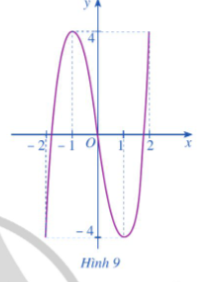
Cho hàm số có đồ thị là đường cong ở Hình 9.
a) Dựa vào đồ thị ở Hình 9, hãy cho biết các giá trị bằng bao nhiêu.
b) Giải phương trình với
c) Tính các giá trị của hàm số tại hai đầu mút và tại các điểm mà ở đó
d) So sánh M (hoặc m) với số lớn nhất (hoặc số bé nhất) trong các giá trị tính được ở câu c
Giải Toán 12 (Cánh Diều) Bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
Kính viễn vọng không gian Hubble được đưa vào vũ trụ ngày 24/4/1990 bằng tàu con thoi Discovery. Vận tốc của tàu con thoi trong sứ mệnh này, từ lúc cất cánh tại thời điểm cho đến khi tên lửa đẩy được phóng đi tại thời điểm , cho bởi hàm số sau:
.
(v được tính bằng ft/s, 1 feet = 0,3048 m)
Hỏi gia tốc của tàu con thoi sẽ tăng trong khoảng thời gian nào tính từ thời điểm cất cánh cho đến khi tên lửa đẩy được phóng đi?
Giải Toán 12 (Cánh Diều) Bài 1: Tính đơn điệu của hàm số
a) Nêu định nghĩa hàm số đồng biến, hàm số nghịch biến trên tập , trong đó K là một khoảng, đoạn hoặc nửa khoảng.
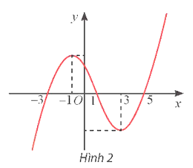
b) Cho hàm số có đồ thị như Hình 2.
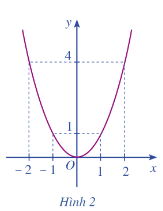
- Xác định khoảng đồng biến, nghịch biến của hàm số đó.
- Xét dấu đạo hàm .
- Nêu mối liên hệ giữa sự đồng biến, nghịch biến của hàm số và dấu của đạo hàm trên mỗi khoảng .
- Hoàn thành bảng biến thiên sau:
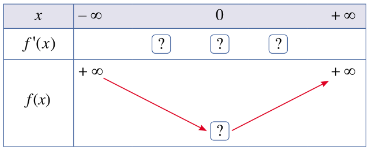
Giải Toán 12 (Cánh Diều) Bài 1: Tính đơn điệu của hàm số
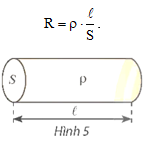
Điện trở R(Ω) của một đoạn dây dẫn hình trụ được làm từ vật liệu có điện trở suất ρ (Ωm), chiều dài ℓ (m) và tiết diện S (m2) được cho bởi công thức
(Vật lí 11 — Chân trời sáng tạo, Nhà xuất bản Giáo dục Việt Nam, 2023, trang 104)
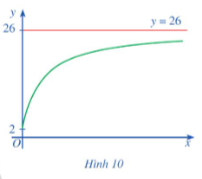
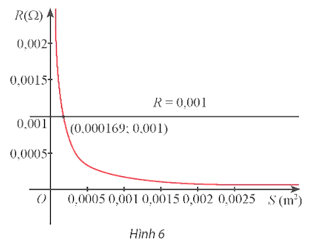
Giả sử người ta khảo sát sự biến thiên của điện trở R theo tiết diện S (ở nhiệt độ 20 °C) của một sợi dây điện dài 10 m làm từ kim loại có điện trở suất ρ và thu được đồ thị hàm số như Hình 6.
a) Có nhận xét gì về sự biến thiên của điện trở R theo tiết điện S?
b) Từ đồ thị, hãy giải thích ý nghĩa của toạ độ giao điểm của đồ thị hàm số với đường thẳng R = 0,001.
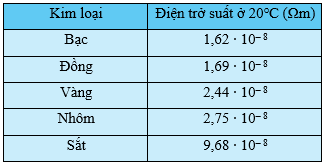
c) Tính điện trở suất ρ của dây điện. Từ đó, hãy cho biết dây điện được làm bằng kim loại nào trong số các kim loại được cho ở bảng sau:
Giải Toán 12 (Chân trời sáng tạo) Bài tập cuối chương 1 trang 37
Trong một nhà hàng, mỗi tuần để chế biến x phần ăn (x lấy giá trị trong khoảng từ 30 đến 120) thì chi phí trung bình (đơn vị: nghìn đồng) của một phần ăn được cho bởi công thức:
a) Khảo sát và vẽ đồ thị hàm số trên [30; 120].
b) Từ kết quả trên, tìm số phần ăn sao cho chi phí trung bình của một phần ăn là thấp nhất.
Giải Toán 12 (Chân trời sáng tạo) Bài tập cuối chương 1 trang 37
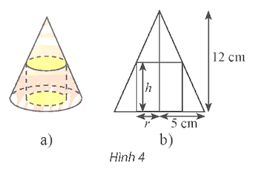
Cho một hình trụ nội tiếp trong hình nón có chiều cao bằng 12 cm và bán kính đáy bằng 5 cm (Hình 4a). Người ta cắt hình nón, trụ này theo mặt phẳng chứa đường thẳng nối đỉnh và tâm hình tròn đáy của hình nón thì thu được một hình phẳng như Hình 4b.
a) Chứng minh rằng công thức tính bán kính r của đáy hình trụ theo chiều cao h của nó là: .
b) Chứng minh biểu thức sau biểu thị thể tích khối trụ theo h: .
c) Tìm h để khối trụ có thể tích lớn nhất.
Giải Toán 12 (Chân trời sáng tạo) Bài tập cuối chương 1 trang 37
Cho hàm số .
a) Khảo sát và vẽ đồ thị của hàm số.
b) Gọi A là giao điểm của đồ thị hàm số với trục Oy, I là giao điểm của hai đường tiệm cận của đồ thị hàm số. Tìm điểm B đối xứng với A qua I. Chứng minh rằng điểm B cũng thuộc đồ thị hàm số này.
Giải Toán 12 (Chân trời sáng tạo) Bài tập cuối chương 1 trang 37
Cho hàm số . Trong các khẳng định sau, khẳng định nào đúng?
A. Hàm số đồng biến trên (– ∞; – 4) và nghịch biến trên (– 4; + ∞).
B. Hàm số đồng biến trên (– ∞; 4) và (4; + ∞).
C. Hàm số nghịch biến trên (– ∞; 4) và (4; + ∞).
D. Hàm số nghịch biến trên (– ∞; – 4) và (– 4; + ∞).
Giải Toán 12 (Chân trời sáng tạo) Bài tập cuối chương 1 trang 37
Cho hàm số . Trong các khẳng định sau, khẳng định nào đúng?
A. Hàm số đạt cực tiểu tại x = 3, giá trị cực tiểu là y = 2.
B. Hàm số đạt cực tiểu tại x = 5, giá trị cực tiểu là y = 6.
C. Hàm số đạt cực tiểu tại x = 3, giá trị cực tiểu là y = 6.
D. Hàm số đạt cực tiểu tại x = 5, giá trị cực tiểu là y = 2.
Giải Toán 12 (Chân trời sáng tạo) Bài tập cuối chương 1 trang 37