Câu hỏi:
128 lượt xemHoạt động 2 trang 31 Toán 10 Tập 2:
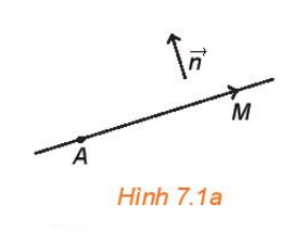
Trong mặt phẳng toạ độ, cho đường thẳng ∆ đi qua điểm A(x0; y0) và có vectơ pháp tuyến (a; b). Chứng minh rằng điểm M(x; y) thuộc ∆ khi và chỉ khi
a(x – x0) + b(y – y0) = 0
Lời giải
Hướng dẫn giải:
Lời giải:
* Giả sử M(x; y) thuộc đường thẳng ∆, ta cần chứng minh: a(x – x0) + b(y – y0) = 0
Vì M ∈ ∆ nên
. = 0
Mà = (x – x0; y – y0) và (a; b)
a(x – x0) + b(y – y0) = 0 (đpcm) (1)
* Giả sử, với M(x; y) thỏa mãn a(x – x0) + b(y – y0) = 0; ta cần chứng minh M thuộc đường thẳng ∆
Theo giả thiết ta có: a(x – x0) + b(y – y0) = 0
Mà = (x – x0; y – y0) và (a; b)
Nên . = 0 hay
Do đó là vectơ pháp tuyến của đường thẳng AM
Mặt khác cũng là vectơ pháp tuyến của đường thẳng ∆
Suy ra đường thẳng AM và đường thẳng ∆ có giá song song hoặc trùng nhau.
Vì đường thẳng ∆ đi qua A nên đường thẳng AM trùng ∆.
Hay điểm M cũng thuộc đường thẳng ∆ (đpcm) (2)
Từ (1) và (2) ta có: điểm M(x; y) thuộc ∆ khi và chỉ khi a(x – x0) + b(y – y0) = 0.
Bài 7.2 trang 34 Toán 10 Tập 2:
Lập phương trình tổng quát của các trục toạ độ