Câu hỏi:
154 lượt xemGiải Toán 10 trang 86 Tập 2
Luyện tập 4 trang 86 Toán 10 Tập 2: Có ba hộp A, B, C. Hộp A có chứa ba thẻ mang số 1, số 2, số 3. Hộp B chứa hai thẻ mang số 2 và số 3. Hộp C chứa hai thẻ mang số 1 và số 2. Từ mỗi hộp ta rút ra ngẫu nhiên một thẻ.
a) Vẽ sơ đồ cây để mô tả các phần tử của không gian mẫu.
b) Gọi M là biến cố: “Trong ba thẻ rút ra có ít nhất một thẻ số 1”. Biến cố là tập con nào của không gian mẫu?
c) Tính P(M) và P()
Lời giải
Hướng dẫn giải:
Lời giải
a) Kí hiệu 1, 2, 3 tương ứng là thẻ mang số 1, 2, 3. Khi đó ta có sơ đồ hình cây mô tả các phần tử của không gian mẫu như sau:
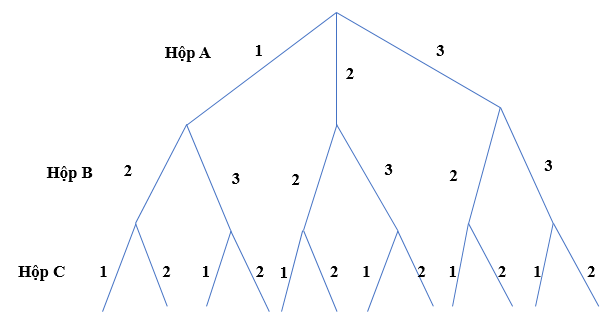
Các kết quả có thể khi rút mỗi hộp một thẻ là: 121; 122; 131; 132; 221; 222; 231; 232; 321; 322; 331; 332.
⇒ Ω ={121; 122; 131; 132; 221; 222; 231; 232; 321; 322; 331; 332}
⇒ n(Ω) = 12.
b) M là biến cố: “Trong ba thẻ rút ra có ít nhất một thẻ số 1”.
Khi đó M không xảy ra khi trong ba thẻ rút ra không có thẻ số 1.
Suy ra biến cố đối của biến cố M là : “Trong ba thẻ rút ra không có thẻ số 1”.
⇒ = {222; 232; 322; 332}
c) Với = {222; 232; 322; 332}
⇒ n() = 4.
⇒ .
Mặt khác, ta có P() = 1 – P(M)
⇒ P(M) = 1 – P() = 1 – = .
Vậy P(M) = , P() = .