30 câu Trắc nghiệm Phân tích một số ra thừa số nguyên tố (có đáp án 2024) – Toán 6 Cánh diều
Bộ 30 câu hỏi trắc nghiệm Toán 6 (có đáp án) Bài 11: Phân tích một số ra thừa số nguyên tố đầy đủ các mức độ sách Cánh diều giúp học sinh ôn luyện trắc nghiệm Toán 6 Bài 11.
Trắc nghiệm Toán lớp 6 Bài 11: Phân tích một số ra thừa số nguyên tố
Câu 1: Chọn đáp án đúng. Phân tích một số tự nhiên lớn hơn 1 ra thừa số nguyên tố là
A. viết số đó dưới dạng một tổng các số nguyên tố
B. viết số đó dưới dạng một hiệu các số nguyên tố
C. viết số đó dưới dạng một thương các số nguyên tố
D. viết số đó dưới dạng một tích các thừa số nguyên tố
Lời giải
Theo lý thuyết: Phân tích một số tự nhiên lớn hơn 1 ra thừa số nguyên tố là viết số đó dưới dạng một tích các thừa số nguyên tố.
Chọn đáp án D
Câu 2: Chọn câu đúng.
A.Mọi số tự nhiên lớn hơn 1 đều phân tích được thành tích các thừa số nguyên tố
B.Chỉ các số nguyên tố mới phân tích được thành tích các số nguyên tố
C.Chỉ các hợp số mới phân tích được thành tích các số nguyên tố
D.Cả A, B, C đều sai
Lời giải
Mọi số tự nhiên lớn hơn 1 đều phân tích được thành tích các thừa số nguyên tố nên A đúng.
Chọn đáp án A.
Câu 3: Phân tích số 24 thành thừa số nguyên tố:
A.24 = 2 . 12
B.24 = 2 + 19 + 3
C.24 = 2 + 2 + 2 + 3
D.24 = 23 . 3
Lời giải
Nhận thấy,
+ Đáp án A: 12 không phải số nguyên tố nên A sai
+ Đáp án B và đáp án C là phân tích 24 thành tổng các số hạng nên đây không phải là phân tích một số ra thừa số nguyên tố nên B và C sai
+ Đáp án D: Ta có: 23 . 3 = 8 . 3 = 24, hơn nữa, 2 và 3 là các số nguyên tố nên đáp án D đúng.
Chọn đáp án D.
Câu 4: Một ước nguyên tố của số 63 là:
A. 1
B. 2
C. 3
D. 5
Lời giải
Trong các đáp án đã cho, ta thấy 1 không phải là số nguyên tố, nên đáp án A sai.
Các số 2, 3, 5 là các số nguyên tố, để tìm ước nguyên tố của 63, ta lần lượt chia 63 cho các số trên, ta thấy 63 chỉ chia hết cho 3 (theo dấu hiệu chia hết).
Vậy một ước nguyên tố của 63 là 3.
Chọn đáp án C.
Câu 5: Phân tích số a ra thừa số nguyên tố, ta được a = p1m1.p2m2 ...pkmk , khẳng định nào sau đây đúng?
A. Các số p1; p2; ...; pk là các số dương
B. Các số p1; p2; ...; pk là các số nguyên tố
C. Các số p1; p2; ...; pk là các số tự nhiên
D. Các số p1; p2; ...; pk tùy ý
Lời giải
Khi phân tích một số a = p1m1.p2m2 ...pkmk ra thừa số nguyên tố thì p1; p2; ...; pk là các số nguyên tố.
Chọn đáp án B.
Câu 6: Phân tích số 18 ra thừa số nguyên tố.
A. 18 = 18 . 1
B. 18 = 10 + 8
C. 18 = 2 . 32
D. 18 = 6 + 6 + 6
Lời giải
+ Đáp án A sai vì 1 không phải là số nguyên tố
+ Đáp án B sai vì đây là phép cộng
+ Đáp án C đúng vì 2 và 3 là hai số nguyên tố nên 18 = 2 . 32
+ Đáp án D sai vì đây là phép cộng
Chọn đáp án C.
Câu 7: Phân tích số 145 ra thừa số nguyên tố.
A. 145 = 1 . 5 . 29
B. 145 = 5 . 29
C. 145 = 5 . 2 . 9
D. 145 = 2 . 3 . 5 . 9
Lời giải
Ta có thể phân tích số 145 ra thừa số bằng cách viết “rẽ nhánh” hoặc “theo cột dọc”.
Phân tích số 145 ra thừa số nguyên tố theo cột dọc như sau:

Vậy 145 = 5 . 29.
Chọn đáp án B.
Câu 8: Cho a2 . b . 7 = 140, với a, b là các số nguyên tố. Vậy a có giá trị bằng bao nhiêu?
A. 1
B. 2
C. 3
D. 4
Lời giải
Ta có a2 . b . 7 = 140
Suy ra: a2 . b = 140 : 7 = 20 = 4 . 5 = 22 . 5
Vậy giá trị của a là 2.
Chọn đáp án B.
Câu 9: Khi phân tích các số 2 150; 1 490; 2 340 ra thừa số nguyên tố thì số nào có chứa tất cả các thừa số nguyên tố 2, 3 và 5?
A. 2 340
B. 2 150
C. 1 490
D. Cả ba số trên
Lời giải
Cách 1: Ta phân tích các số 2 150; 1 490; 2 340 ra thừa số nguyên tố.
Ta có:
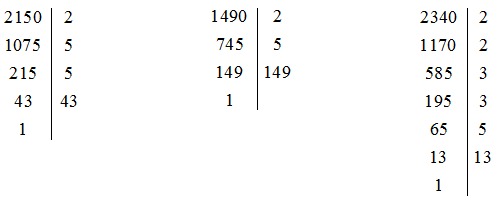
Do đó: 2 150 = 2 . 5 . 5 . 43 = 2 . 52 . 43
1 490 = 2 . 5 . 149
2 340 = 2 . 2 . 3 . 3 . 5 . 13 = 22 . 32 . 5 . 13
Vậy ta thấy trong các số đã cho, khi phân tích ra thừa số nguyên tố, chỉ có số 2 340 là có chứa tất cả các thừa số nguyên tố 2, 3 và 5.
Cách 2: Ta áp dụng dấu hiệu chia hết, thấy số 2 340 chia hết cho cả 2, 3 và 5 nên thỏa mãn yêu cầu bài toán.
Chọn đáp án A.
Câu 10: Số 360 khi phân tích được thành thừa số nguyên tố, hỏi tích đó có bao nhiêu thừa số là số nguyên tố?
A. 3
B. 4
C. 5
D. 6
Lời giải
Ta phân tích 360 ra thừa số nguyên tố bằng cách viết rẽ nhánh như sau:
Ta có: 360 = 36 . 10
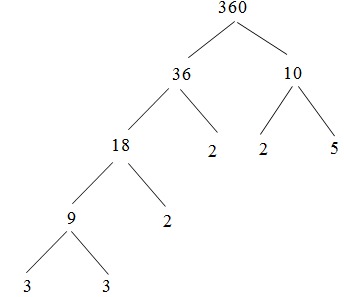
Do đó: 360 = 2 . 2 . 2 . 3 . 3 . 5 = 23 . 32 . 5
Vậy khi phân tích 360 ra thừa số nguyên tố, tích đó có ba thừa số là số nguyên tố.
Chọn đáp án A.
Câu 11: Trong các số sau, số nào là tích của ba số tự nhiên liên tiếp?
A. 2 279
B. 46 620
C. 3 953
D. 6 059
Lời giải
Phân tích các số đã cho ra thừa số nguyên tố sau đó phân tích thành tích, ta được:
2 279 = 43 . 53
46 620 = 22 . 32 . 5 . 7 . 37 = (5 . 7) . (22 . 32) . 37 = 35 . 36 . 37
3 953 = 59 . 67
6 059 = 73 . 83
Vậy số 46 620 phân tích được thành tích ba số tự nhiên liên tiếp.
Chọn đáp án B.
Câu 12: Một hình vuông có diện tích là 5 929 m2. Tính cạnh của hình vuông đó.
A. 44
B. 77
C. 73
D. 69
Lời giải
Ta phân tích số 5 929 ra thừa số nguyên tố:

Do đó: 5 929 = 7 . 7 . 11 . 11 = 72 . 112 = (7 . 11) . (7 . 11) = 77 . 77.
Vậy cạnh của hình vuông bằng 77 m.
Chọn đáp án B.
Câu 13: Hãy viết tập hợp A tất cả các ước của 24 :
A. A = {1; 2}
B. A = {1; 2; 4}
C. A = {1; 2; 4; 8}
D. A = {1; 2; 4; 8; 16}
Lời giải
Các ước của 24 là: 1; 2; 22 = 4; 23 = 8; 2 4 = 16
Vậy các ước của 24 là 1, 2, 4, 8, 16.
Do đó ta viết tập hợp A: A = {1; 2; 4; 8; 16}.
Chọn đáp án D.
Câu 14: Cho số 150 = 2 . 3 . 52, số lượng ước của 150 là bao nhiêu?
A. 6
B. 7
C. 8
D. 12
Lời giải
Lý thuyết: Nếu m = ax . by . cz, với a, b, c là số nguyên tố thì m có (x + 1)(y + 1)(z + 1) ước.
Phân tích số 150 ra thừa số nguyên tố:

Ta có: 150 = 2 . 3 . 52 với x = 1; y = 1; z = 2
Vậy số lượng ước số của 150 là (1 + 1)(1 + 1)(2 + 1) = 12 ước.
Chọn đáp án D.
Câu 15: Cho a = 22 . 7, hãy viết tập hợp Ư(a) tất cả các ước của a.
A. Ư(a) = {4; 7}
B. Ư(a) = {1; 4; 7}
C. Ư(a) = {1; 2; 4; 7; 28}
D. Ư(a) = {1; 2; 4; 7; 14; 28}
Lời giải
Ta có: a = 22 . 7 = 4 . 7 = 28
28 = 28 . 1 = 14 . 2 = 7 . 4 = 7 . 2 . 2
Do đó ta tìm được các ước của 28 là: 1, 2, 4, 7, 14, 28.
Vậy Ư(28) = {1; 2; 4; 7; 14; 28}.
Chọn đáp án D.
Câu 16: Trong các số tự nhiên sau, số có ước nhiều nhất là:
A. 1 464
B. 496
C. 1 035
D. 1 517
Lời giải
Lý thuyết: Nếu m = ax . by . cz, với a, b, c là số nguyên tố thì m có (x + 1)(y + 1)(z + 1) ước.
Vậy ta phân tích các số đã cho ra thừa số nguyên tố rồi tìm các ước của số đó.
1 464 = 23 . 3 . 61 có (3 + 1)(1 + 1)(1 + 1) = 16 ước
496 = 24 . 31 có (4 + 1)(1 + 1) = 10 ước
1 035 = 32 . 5 . 23 có (2 + 1)(1 + 1)(1 + 1) = 12 ước
1 517 = 37 . 41 có (1 + 1)(1 + 1) = 4 ước
Vậy số tự nhiên có ước nhiều nhất là 1 464.
Chọn đáp án A.
Câu 17: Tìm số tự nhiên n biết 1 + 2 + 3 + ... + n = 465.
A. 27
B. 28
C. 29
D. 30
Lời giải
Ta tính tổng: 1 + 2 + 3 + … + n
Ta thấy tổng trên có: (n – 1) : 1 + 1 = n (số hạng)
Do đó: 1 + 2 + 3 + … + n = n . (n + 1) : 2
Theo đề bài ta được: n . (n + 1) : 2 = 465
Suy ra: n . (n + 1) = 465 . 2 = 930
Nhận thấy tích n . (n + 1) là tích của hai số tự nhiên liên tiếp.
Do đó ta phân tích 930 ra thừa số nguyên tố sau đó phân tích thành tích, ta được:
930 = 2 . 3 . 5 . 31 = (2 . 3 . 5) . 31 = 30 . 31 = 30 . (30 + 1)
Khi đó: n . (n + 1) = 30 . (30 + 1)
Vậy n = 30.
Chọn đáp án D.