30 câu Trắc nghiệm Phép nhân và phép chia các số tự nhiên (có đáp án 2024) – Toán 6 Cánh diều
Bộ 30 câu hỏi trắc nghiệm Toán 6 (có đáp án) Bài 4: Phép nhân và phép chia các số tự nhiên đầy đủ các mức độ sách Cánh diều giúp học sinh ôn luyện trắc nghiệm Toán 6 Bài 4.
Nội dung bài viết
Xem thêm »
Trắc nghiệm Toán lớp 6 Bài 4: Phép nhân và phép chia các số tự nhiên
Phần 1. Trắc nghiệm Phép nhân và phép chia các số tự nhiên
Câu 1: Tìm số tự nhiên x, biết: (x – 5) . 1 000 = 0.
A. x = 5
B. x = 1 000
C. x = 7
D. x = 5 000
Lời giải
Ta có: (x – 5) . 1 000 = 0
x – 5 = 0 : 1000
x – 5 = 0
x = 0 + 5
x = 5
Vậy x = 5.
Chọn đáp án A.
Câu 2: Kết quả của phép tính 159 . 57 – 59 . 57 là:
A. 57
B. 157
C. 570
D. 5 700
Lời giải
Ta có: 159 . 57 – 59 . 57
= (159 – 59) . 57 (tính chất phân phối của phép nhân với phép trừ)
= 100 . 57
= 5 700
Chọn đáp án D.
Câu 3: Số tự nhiên x nào dưới đây thỏa mãn: 2 021 . (x – 2 021) = 2 021.
A. 2 020
B. 2 021
C. 2 022
D. 2 023
Lời giải
Ta có: 2 021 . (x – 2 021) = 2 021
x – 2 021 = 2 021 : 2 021
x – 2 021 = 1
x = 1 + 2 021
x = 2 022
Vậy x = 2 022.
Chọn đáp án C.
Câu 4: Kết quả của phép tính 12 . 100 + 100 . 36 – 100 . 19 là:
A. 29 000
B. 3 800
C. 290
D. 2 900
Lời giải
Ta có:
12 . 100 + 100 . 36 – 100 . 19
= 100 . 12 + 100 . 36 – 100 . 19
= 100 . (12 + 36 – 19)
= 100 . 29 = 2 900
Chọn đáp án D.
Câu 5: Thực hiện phép tính (56 . 35 + 56 . 18) : 53 ta được kết quả là:
A. 12
B. 28
C. 53
D. 56
Lời giải
Ta có: (56 . 35 + 56 . 18) : 53
= [56 . (35 + 18)] : 53
= 56 . 53 : 53
= 56 . (53 : 53)
= 56 . 1
= 56
Chọn đáp án D.
Câu 6: Thương của phép chia số 785 cho số 5 là:
A. 157
B. 175
C. 177
D. 155
Lời giải
Ta thực hiện phép chia 785 : 5 bằng cách đặt tính chia như sau:
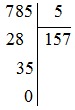
Vậy 785 : 5 = 157.
Chọn đáp án A.
Câu 7: Số thích hợp điền vào dấu ? trong phép tính: a : 1 = ? là:
A. 1
B. 2
C. a
D. 0
Lời giải
Ta có: a : 1 = a (Một số tự nhiên bất kì chia cho 1 thì bằng chính nó).
Chọn đáp án C.
Câu 8: Kết quả của phép tính 0 : a (với a ≠ 0) là:
A. 0
B. 1
C. 2
D. a
Lời giải
Ta có: 0 : a = 0 (với a ≠ 0)
Số 0 chia cho bất kì số tự nhiên nào khác 0 cũng bằng 0.
Chọn đáp án A.
Câu 9: Cho r là số dư trong phép chia a cho b (với b ≠ 0). Khi đó:
A. r = b
B. r > b
C. r > 0
D. 0 ≤ r < b
Lời giải
Trong phép chia, số dư luôn lớn hơn hoặc bằng 0 và nhỏ hơn số chia.
Do đó: r là số dư của phép chia a cho b (với b ≠ 0) thì 0 ≤ r < b.
Chọn đáp án D.
Câu 10: Cho phép tính 12 × 5 = 60. Chọn câu sai.
A. 12 là thừa số
B. 5 là thừa số
C. 60 là tích
D. 60 là thương
Lời giải
Trong phép tính 12 × 5 = 60, có 12 và 5 là các thừa số và 60 là tích.
Vậy đáp án A, B, C đúng và D sai.
Chọn đáp án D.
Câu 11: Kết quả của phép tính 121 × 289 là:
A. 34 969
B. 34 699
C. 43 969
D. 32 969
Lời giải
Ta đặt tính để tính tích như sau:
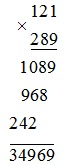
Vậy 121 × 289 = 34 969.
Chọn đáp án A.
Câu 12: Kết quả của phép tính 25 . 12 . 4 là:
A. 1 000
B. 1 200
C. 120
D. 12 000
Lời giải
Ta có: 25 . 12 . 4 = 25 . 4 . 12 = (25 . 4) . 12 = 100 . 12 = 1 200
Chọn đáp án B.
Câu 13: Phép chia a : b thực hiện được khi:
A. b là số tự nhiên bất kì
B. b = 0
C. b ≠ 0
D. b ≠ 1
Lời giải
Phép chia a : b thực hiện được khi số chia b phải khác 0, tức là b ≠ 0.
Chọn đáp án C.
Câu 14: Cho phép tính: 10 789 : 123. Chọn kết luận đúng.
A. Số 10 789 được gọi là số bị chia
B. Số 123 được gọi là số bị chia
C. Số 10 789 được gọi là số chia
D. Số 123 được gọi là thương
Lời giải
Phép tính 10 789 : 123 có 10 789 là số bị chia và 123 là số chia.
Chọn đáp án A.
Câu 15. Kết quả của phép tính 879 . 2a + 879 . 5a + 879 . 3a là
A. 8 790
B. 87 900a
C. 8 790a
D. 8 79a
Lời giải
Ta có:
879 . 2a + 879 . 5a + 879 . 3a
= 879 . (2a + 3a + 5a)
= 879 . (2 + 3 + 5)a
= 879 . 10a
= 8 790a
Chọn đáp án C.
Câu 16: Không tính giá trị cụ thể, hãy so sánh A = 1 987 657 . 1 987 655 và B = 1 987 656 . 1 987 656.
A. A > B
B. A < B
C. A ≤ B
D. A = B
Lời giải
Ta có:
A = 1 987 657 . 1 987 655
= (1 987 656 + 1) . 1 987 655
= 1 987 656 . 1 987 655 + 1 987 655
B = 1 987 656 . 1 987 656
= 1 987 656 . (1 987 655 + 1)
= 1 987 656 . 1 987 655 + 1 987 656
Vì 1 987 655 < 1 987 656
Nên 1 987 656 . 1 987 655 + 1 987 655 < 1 987 656 . 1 987 655 + 1 987 656
Khi đó A < B.
Chọn đáp án B.
Câu 17: Một quyển vở kẻ ngang 200 trang có giá 18 000 đồng. Với 400 000 đồng, bạn có thể mua được nhiều nhất bao nhiêu quyển vở loại này?
A. 23 quyển vở
B. 22 quyển vở
C. 21 quyển vở
D. 20 quyển vở
Lời giải
Một quyển vở kẻ ngang 200 trang có giá 18 000 đồng, để biết với 400 000 đồng mua được bao nhiêu quyển vở như trên, ta cần thực hiện phép chia 400 000 cho 18 000, ta có:
400 000 : 18 000 = 22 (dư 4 000)
Dư 4 000 đồng không thể mua thêm một quyển vở được.
Vậy với 400 000 đồng, bạn có thể mua được nhiều nhất 22 quyển vở.
Chọn đáp án B.
Câu 18: Một hình chữ nhật có chiều dài bằng 15 cm, diện tích bằng a cm2. Tính chiều rộng của hình chữ nhật này (là một số tự nhiên) nếu biết a là một số tự nhiên từ 126 đến 137.
A. 8 cm
B. 9 cm
C. 10 cm
D. 11 cm
Lời giải
Giả sử chiều rộng của hình chữ nhật là b (với b ∈ N* , b < 15).
Khi đó diện tích hình chữ nhật là S = 15b (cm2)
Mà đề bài cho diện tích hình chữ nhật bằng a cm2 và a là một số tự nhiên từ 126 đến 137 nên ta có: 126 ≤ a ≤ 137
Hay 126 ≤ 15b ≤ 137
Suy ra 126 : 15 ≤ b ≤ 137 : 15
Lại có: 126 : 15 = 8 (dư 6); 137 : 15 = 9 (dư 2)
Do đó b = 9 (t/m).
Vậy chiều rộng hình chữ nhật là 9 cm.
Chọn đáp án B.
Câu 19: Tính nhanh 125 . 1 975 . 4 . 8 . 25?
A. 1 975 000 000
B. 1 975 000
C. 19 750 000
D. 197 500 000
Lời giải
Ta có:
125 . 1 975 . 4 . 8 . 25
= 1 975 . (125 . 8) . (25 . 4)
= 1 975 . 1 000 . 100
= 1 975 000 . 100
= 197 500 000.
Chọn đáp án D.
Câu 20: Thực hiện phép chia 1 245 cho 67 được số dư là:
A. 67
B. 39
C. 93
D. 29
Lời giải
Ta đặt tính chia như sau:
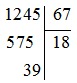
Vậy 1 245 : 67 = 18 (dư 39).
Chọn đáp án B.
Phần 2. Lý thuyết Phép nhân và phép chia các số tự nhiên
I. Phép nhân
1. Phép nhân hai số tự nhiên
a x b = c
(thừa số) x (thừa số) = (tích)
Ví dụ: 5 x 2 = 10; 20 x 3 = 60
Quy ước:
+ Trong một tích, ta có thể thay dấu nhân “x” bằng dấu chấm “.”
Ví dụ: 5 x 2 = 5 . 2
+ Trong một tích mà các thừa số đều bằng chữ hoặc chỉ có một thừa số bằng số, ta có thể không cần viết dấu nhân giữa các thừa số
Ví dụ: a x b = a . b = ab hoặc 4. a . b = 4ab
+ Khi nhân hai số có nhiều chữ số, thông thường đặt tính rồi tính, chú ý khi viết các tích riêng (tích riêng thứ hai lùi sang bên trái một cột so với tích riêng thứ nhất, tích riêng thứ ba lùi sang bên trái hai cột so với tích riêng thứ nhất,…)
Ví dụ: Đặt tính rồi tính: 341 x 157
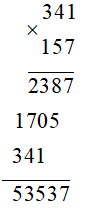
Vậy 341 x 157 = 53 537.
2. Tính chất của phép nhân
Phép nhân các số tự nhiên có các tính chất sau:
+ Giao hoán: a . b = b . a
+ Kết hợp: (a . b) . c = a . (b . c)
+ Nhân với số 1: a . a = 1 . a = a
+ Phân phối đối với phép cộng và phép trừ:
a . (b + c) = a. b + a . c
a . (b – c) = a . b – a . c
Chú ý: Do tính chất kết hợp nên giá trị của biểu thức a. b. c có thể được tính theo một trong hai cách sau:
a . b. c = (a . b) . c hoặc a . b . c = a . (b . c)
Ví dụ: Tính một cách hợp lý:
a) 20 . 36 . 5
b) 34 . 28 + 34 . 72
Lời giải:
a) 20 . 36 . 5
= 20 . 5 . 36 (tính chất giao hoán)
= (20 . 5) . 36 (tính chất kết hợp)
= 100 . 36
= 3 600
b) 34 . 28 + 34 . 72
= 34 . (28 + 72)
= 34 . 100
= 3 400
II. Phép chia
1. Phép chia hết
a : b = q (b#0)
(số bị chia) : (số chia) = (thương)
Ví dụ: 10 : 2 = 5; 30 : 5 = 6
Chú ý:
+ Nếu a : b = q thì q = bq
+ Nếu a : b = q và q 0 thì a : q = b
+ Thông thường, ta đặt tính chia để thực hiện phép chia.
Ví dụ: Đặt tính để tính thương: 139 004 : 236.
Lời giải:
Ta có:
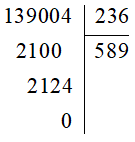
Vậy 139 004 : 236 = 589.
2. Phép chia có dư
Cho hai số tự nhiên a và b với . Khi đó luôn tìm được đúng hai số tự nhiên q và r sao cho a = b . q + r, trong đó .
Chú ý:
+ Khi r = 0 ta có phép chia hết.
+ Khi r # 0 ta có phép chia có dư. Ta nói: a chia cho b được thương là q và số dư là r.
Kí hiệu: a : b = q (dư r)
Ví dụ: Đặt tính để tính thương và số dư của phép chia:
5 125 : 320.
Lời giải:
Ta có:
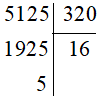
Vậy 5 125 : 320 = 16 (dư 5).