30 câu Trắc nghiệm Phép tính lũy thừa với số mũ tự nhiên (có đáp án 2024) – Toán 6 Cánh diều
Bộ 30 câu hỏi trắc nghiệm Toán 6 (có đáp án) Bài 5: Phép tính lũy thừa với số mũ tự nhiên đầy đủ các mức độ sách Cánh diều giúp học sinh ôn luyện trắc nghiệm Toán 6 Bài 5.
Trắc nghiệm Toán lớp 6 Bài 5: Phép tính lũy thừa với số mũ tự nhiên
Phần 1. Trắc nghiệm Phép tính lũy thừa với số mũ tự nhiên
Câu 1: Viết tích sau dưới dạng lũy thừa: 6 . 6 . 6 . 6 . 6
A. 66
B. 65
C. 56
D. 64
Lời giải
Ta có: 6.6.6.6.6 = 65 (tích của 5 thừa số 6).
Chọn đáp án B.
Câu 2: Chọn câu đúng.
A. am . an = am + n
B. a . a . a . a . a = 5a
C. am . an = am.n
D. a1 = 1
Lời giải
Ta có với a, m, n ∈ N thì:
+) am . an = am + n (nhân hai lũy thừa cùng cơ số) nên A đúng và C sai.
+) a . a . a . a . a = a5 (tích của 5 thừa số a) nên B sai.
+) a1 = a nên D sai.
Chọn đáp án A.
Câu 3: Chọn câu sai. Cho lũy thừa: 25 thì
A. 2 là cơ số
B. 5 là số mũ
C. 2 là số mũ
D. 25 = 32
Lời giải
Ta có: với lũy thừa 25 thì 2 được gọi là cơ số, 5 được gọi là số mũ nên đáp án A, B đúng và đáp án C sai.
Lại có: 25 = 2 . 2 . 2 . 2 . 2 = 4 . 2 . 2 . 2 = 8 . 2 . 2 = 16 . 2 = 32 nên đáp án D đúng.
Chọn đáp án C.
Câu 4: Chọn câu sai. 38 được đọc là:
A. ba mũ tám
B. ba lũy thừa tám
C. lũy thừa bậc tám của ba
D. tám mũ ba
Lời giải
Ta có: 38 đọc là “ba mũ tám” hoặc “ba lũy thừa tám” hoặc “lũy thừa bậc tám của ba” nên đáp án A, B, C đúng và D sai.
Chọn đáp án D.
Câu 5: Viết số 81 dưới dạng lũy thừa. Chọn câu sai.
A. 34
B. 92
C. 811
D. 29
Lời giải
Ta có: 81 = 811
81 = 9 . 9 = 92
81 = 3 . 3 . 3 . 3 = 34
Vậy viết 81 dưới dạng lũy thừa, ta được: 81 = 811 = 92 = 34.
Do đó đáp án A, B, C đúng và D sai.
Chọn đáp án D.
Câu 6: Chọn đáp án sai.
A. 53 < 35
B. 34 > 25
C. 43 = 26
D. 43 > 82
Lời giải
Ta có:
+) 53 = 125; 35 = 243 suy ra 53 < 35 nên A đúng.
+) 34 = 81; 25 = 32 suy ra 34 > 25 nên B đúng.
+) 43 = 64; 26 = 64 suy ra 43 = 26 nên C đúng.
+) 43 = 64; 82 = 64 suy ra 43 = 82 nên D sai.
Chọn đáp án D.
Câu 7: Tìm số tự nhiên n thỏa mãn 3n = 81.
A. n = 2
B. n = 3
C. n = 4
D. n = 8
Lời giải
Ta có: 34 = 81 nên 3n = 34, do đó n = 4.
Chọn đáp án C.
Câu 8: Viết cấu tạo số 2 017 dưới dạng tổng các lũy thừa của 10 là:
A. 2 017 = 2 . 104 + 102 + 7 . 100
B. 2 017 = 2 . 103 + 10 + 7 . 100
C. 2 017 = 2 . 104 + 102 + 7 . 10
D. 2 017 = 2 . 103 + 102 + 7 . 100
Lời giải
Ta có: 2 017 = 2 . 1 000 + 0 . 100 + 1 . 10 + 7 . 1 = 2 . 103 + 10 + 7 . 100.
Chọn đáp án B.
Câu 9: Viết kết quả phép tính 63 . 2 . 64 . 3 dưới dạng một lũy thừa ta được:
A. 66
B. 67
C. 68
D. 69
Lời giải
Ta có: 63 . 2 . 64 . 3 = (63 . 64) . (2 . 3) = 63 + 4 . 6 = 67 . 61 = 67 + 1 = 68.
Chọn đáp án C.
Câu 10: Chọn kết luận đúng trong các kết luận sau:
A. 33 . 34 = 312
B. 30 = 0
C. 42 : 23 = 2
D. 55 : 5 = 14
Lời giải
Ta có:
33 . 34 = 33 + 4 = 37 nên đáp án A sai
30 = 1 (quy ước) nên đáp án B sai
42 : 23 = 4 . 4 : 23 = 2 . 2 . 2 . 2 : 23 = 24. 23 = 24 – 3 = 21 = 2 nên C đúng
55 : 5 = 55 – 1 = 54 ≠ 14 nên D sai
Chọn đáp án C.
Câu 11: Chọn đáp án đúng?
A. 52 . 53 . 54 = 510
B. 52 . 53 . 25 = 57
C. 53 . 5 = 253
D. 51 = 1
Lời giải
Ta có:
+) 52 . 53 . 54 = 52 + 3 + 4 = 59 nên đáp án A sai.
+) 52 . 53 . 25 = 52 . 53 . 5 . 5 = 52 . 53 . 52 = 52 + 3 + 2 = 57 nên đáp án B đúng.
+) 53 . 5 = 53 + 1 = 54 nên đáp án C sai.
+) 51 = 5 nên đáp án D sai.
Chọn đáp án B.
Câu 12: Tính 24 + 16 ta được kết quả dưới dạng lũy thừa là?
A. 220
B. 24
C. 25
D. 210
Lời giải
Ta có: 24 + 16 = 24 + 2 . 2 . 2 . 2 = 24 + 24 = 2 . 24 = 21 + 4 = 25
Chọn đáp án C.
Câu 13: Số tự nhiên được biểu diễn bởi 2 . 103 + 7 . 102 + 8 . 10 + 7 . 100 là:
A. 2 787
B. 2 7870
C. 278
D. 2 780
Lời giải
Ta có:
2 . 103 + 7 . 102 + 8 . 10 + 7 . 100
= 2 . 1 000 + 7 . 100 + 8 . 10 + 7 . 1
= 2 000 + 700 + 80 + 7 = 2 787
Chọn đáp án A
Câu 14: Số tự nhiên n thỏa mãn 2n = 42 là:
A. n = 3
B. n = 4
C. n = 5
D. n = 6
Lời giải
Ta có:
42 = 4 . 4 = 2 . 2 . 2 . 2 = 24
Vì 2n = 42 nên 2n = 24
Vậy n = 4.
Chọn đáp án B
Câu 15: Viết kết quả phép tính 122 . 2 . 125 . 6 dưới dạng một lũy thừa, ta được:
A. 129
B. 128
C. 127
D. 126
Lời giải
Ta có: 122 . 2 . 125 . 6 = 122 . 125 . (2 . 6) = 122 + 5 . 12 = 127 . 121 = 127 + 1 = 128.
Chọn đáp án B.
Câu 16: Tìm số tự nhiên n thỏa mãn 25n : 253 = 255?
A. n = 3
B. n = 6
C. n = 7
D. n = 8
Lời giải
Ta có: 25n : 253 = 255
Vì 25n : 253 = 25n – 3
Nên ta được: 25n – 3 = 255
Do đó: n – 3 = 5
Suy ra: n = 5 + 3 = 8
Vậy n = 8.
Chọn đáp án D.
Câu 17: Tìm số tự nhiên n thỏa mãn 4n = 43 . 45?
A. n = 32
B. n = 16
C. n = 8
D. n = 4
Lời giải
Ta có: 43 . 45 = 43 + 5 = 48 nên 4n = 48 suy ra n = 8.
Chọn đáp án C.
Câu 18: Tìm số tự nhiên m thỏa mãn 202018 < 20m < 202020 ?
A. m = 2 020
B. m = 2 019
C. m = 2 018
D. m = 20
Lời giải
Ta có: 202018 < 20m < 202020
Suy ra: 2 018 < m < 2 020
Mà m là số tự nhiên nên m = 2 019.
Vậy m = 2 019.
Chọn đáp án B.
Câu 19: Không tính các lũy thừa, hãy so sánh A và B với A = 2711 và B = 818.
A. A = B
B. A > B
C. A < B
D. A ≤ B
Lời giải
Ta có: A = 2711 = (3 . 3 . 3)11 = (33)11 =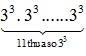 
= 
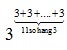= 33 . 11 = 333
Lại có: B = 818 = (3 . 3 . 3 . 3)8 = (34)8 =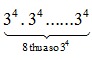 
= 
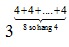= 34 . 8 = 332
Vì 33 > 32 nên 333 > 332 hay 2711 > 818
Vậy A > B.
Chọn đáp án B.
Câu 20: Chữ số tận cùng của số 475 là:
A. 7
B. 5
C. 4
D. 1
Lời giải
Ta có: 47 . 47 = 47 . (40 + 7) = 47 . 40 + 47 . 7
= 47 . 40 + (40 + 7) . 7
= 47 . 40 + 40 . 7 + 7 . 7
Suy ra 47 . 47 có chữ số tận cùng như chữ số tận cùng của 7 . 7 = 49.
Do đó 472 có chữ số tận cùng là 9
Tương tự (472)2 có chữ số tận cùng của 92 = 81.
Mà (472)2 = 472 . 472 = 47 . 47 . 47 . 47 = 474
Do đó 474 có chữ số tận cùng là 1.
Vậy 475 = 474 . 47 có chữ số tận cùng là 1 . 7 = 7.
Chọn đáp án A.
Câu 21: Viết tích 10 . 10 . 10 . 100 dưới dạng lũy thừa cơ số 10, ta được:
A. 104
B. 105
C. 106
D. 107
Lời giải
Ta có: 10 . 10 . 10 . 100 = 10 . 10 . 10 . 10 . 10 = 105
Chọn đáp án B.
Câu 222: Với a ≠ 0 và , ta có: am : an = ?
A. am : n
B. a
C. am – n
D. am + n
Lời giải
Theo công thức chia hai lũy thừa cùng cơ số, ta có:
am : an = am – n (với a ≠ 0 và m ≥ n )
Chọn đáp án C.
23: Tính giá trị của lũy thừa 54 ta được:
A. 20
B. 25
C. 125
D. 625
Lời giải
Ta có: 54 = 5 . 5 . 5 . 5 = 25 . 5 . 5 = 125 . 5 = 625
Chọn đáp án D.
Câu 24: Viết 73 . 77 dưới dạng một lũy thừa ta được:
A. 721
B. 710
C. 74
D. 71
Lời giải
Áp dụng công thức nhân hai lũy thừa cùng cơ số, ta có: 73 . 77 = 73 + 7 = 710.
Chọn đáp án B.
Câu 25: Viết 189 : 183 dưới dạng một lũy thừa ta được:
A. 1812
B. 183
C. 186
D. 1810
Lời giải
Áp dụng công thức chia hai lũy thừa cùng cơ số, ta có: 189 : 183 = 189 – 3 = 186.
Chọn đáp án C.
Phần 2. Lý thuyết Phép tính lũy thừa với số mũ tự nhiên
I. Phép nâng lên lũy thừa
Lũy thừa bậc n của a, kí hiệu , là tích của n thừa số a:
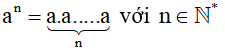
Trong đó:
a được gọi là cơ số
n được gọi là số mũ.
Quy ước: a1=a
Phép nhân nhiều thừa số bằng nhau gọi là phép nâng lên lũy thừa.
Chú ý:
+ an đọc là “a mũ n” hoặc “a lũy thừa n” hoặc “lũy thừa bậc n của a”.
+ a2 còn được gọi là “a bình phương” hay “bình phương của a”.
+ a3 còn được gọi là “a lập phương” hay “lập phương của a”.
Ví dụ:
7 . 7 . 7 . 7 = 74 (đọc là 7 mũ 4 hoặc là 7 lũy thừa 4, hoặc lũy thừa bậc bốn của 7)
16 = 2 . 2 . 2 . 2 = 24
Lưu ý: Với n là số tự nhiên khác 0, ta có: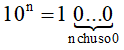 
Ví dụ: 105 = 10 . 10 . 10 . 10 . 10 = 100 000
II. Nhân hai lũy thừa cùng cơ số
Khi nhân hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng các số mũ:
am . an = am + n
Ví dụ:
+) 23 . 24 = 23 + 4 = 27
+) a2 . a1 = a2 + 1 = a3
+) 42 . 45 = 42 + 5 = 47
III. Chia hai lũy thừa cùng cơ số
Khi chia hai lũy thừa cùng cơ số (khác 0), ta giữ nguyên cơ số và trừ các số mũ:
am : an = am - n (a # 0, m ≥ n)
Quy ước: a0 = 1 (a # 0) .
Ví dụ:
+ 97 : 93 = 97 - 3 = 94
+ 76 : 7 = 76 : 71 = 76 - 1 = 75
+ 33 : 33 = 33 - 3 = 30 = 1