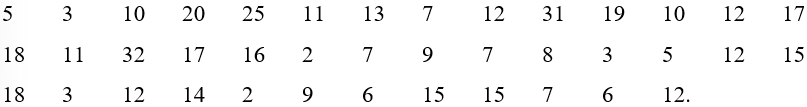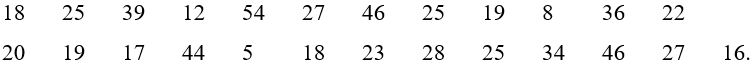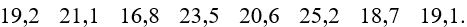Bài 3.6 trang 67 Toán 11 Tập 1: Điểm thi môn Toán (thang điểm 100, điểm được làm tròn đến 1) của 60 thí sinh được cho trong bảng sau:

a) Hiệu chỉnh để thu được mẫu số liệu ghép nhóm dạng Bảng 3.2.

b) Tìm các tứ phân vị và giải thích ý nghĩa của chúng.

Bài 3.5 trang 67 Toán 11 Tập 1: Tuổi thọ (năm) của 50 bình ắc quy ô tô được cho như sau:

a) Xác định mốt và giải thích ý nghĩa.

b) Tính tuổi thọ trung bình của 50 bình ắc quy ô tô này.

Bài tập

Giải Toán 11 trang 67

Bài 3.4 trang 67 Toán 11 Tập 1: Quãng đường (km) đi từ nhà đến nơi làm việc của 40 công nhân một nhà máy được ghi lại như sau:

a) Ghép nhóm dãy số liệu trên thành các khoảng có độ rộng bằng nhau, khoảng đầu tiên là [0; 5). Tìm giá trị đại diện cho mỗi nhóm.

b) Tính số trung bình của mẫu số liệu không ghép nhóm và mẫu số liệu ghép nhóm. Giá trị nào chính xác hơn?

c) Xác định nhóm chứa mốt của mẫu số liệu ghép nhóm thu được.

Vận dụng trang 66 Toán 11 Tập 1: Hãy tính các số đặc trưng cho mẫu số liệu trong Bảng 3.1 và giải thích ý nghĩa của các giá trị thu được.

Luyện tập 4 trang 66 Toán 11 Tập 1: Thời gian (phút) để học sinh hoàn thành một câu hỏi thi được cho như sau:

Tìm mốt của mẫu số liệu ghép nhóm này.

4. Mốt của mẫu số liệu ghép nhóm

Giải Toán 11 trang 66

HĐ4 trang 66 Toán 11 Tập 1: Với số liệu cho trong Luyện tập 1:

a) Có thể tìm được giá trị chính xác cho mốt của mẫu số liệu gốc về thời gian xem ti vi của học sinh không?

b) Mốt thuộc nhóm nào là hợp lí nhất? Nên lấy số nào trong nhóm để ước lượng được cho mốt?

Giải Toán 11 trang 65

Luyện tập 3 trang 65 Toán 11 Tập 1: Tìm tứ phân vị thứ nhất và tứ phân vị thứ ba cho mẫu số liệu ghép nhóm ở Luyện tập 2.

3. Tứ phân vị của mẫu số liệu ghép nhóm

HĐ3 trang 64 Toán 11 Tập 1: Với mẫu số liệu ghép nhóm cho trong HĐ2, hãy cho biết tứ phân vị thứ nhất Q1 và tứ phân vị thứ ba Q3 thuộc nhóm nào.

Giải Toán 11 trang 64

Luyện tập 2 trang 64 Toán 11 Tập 1: Ghi lại tốc độ bóng trong 200 lần giao bóng của một vận động viên môn quần vợt cho kết quả như bảng bên.

Tính trung vị của mẫu số liệu ghép nhóm này.

2. Trung vị của mẫu số liệu ghép nhóm

HĐ2 trang 63 Toán 11 Tập 1: Cho mẫu số liệu ghép nhóm về chiều cao của 21 câu na giống.

Gọi x1, x2, ..., x21 là chiều cao của các cây giống, đã được sắp xếp theo thứ tự tăng dần. Khi đó, x1, ..., x3 thuộc [0; 5), x4, ..., x11 thuộc [5; 10), ... Hỏi trung vị thuộc nhóm nào?

Giải Toán 11 trang 63

Luyện tập 1 trang 63 Toán 11 Tập 1: Tìm hiểu thời gian xem ti vi trong tuần trước (đơn vị: giờ) của một số học sinh thu được kết quả sau:

Tính thời gian xem ti vi trung bình trong tuần trước của các bạn học sinh này.

1. Số trung bình của mẫu số liệu ghép nhóm

HĐ1 trang 62 Toán 11 Tập 1: Khảo sát thời gian tự học của các học sinh trong lớp theo mẫu bên.

a) Hãy lập bảng thống kê cho mẫu số liệu ghép nhóm thu được.

b) Có thể tính chính xác thời gian tự học trung bình của các học sinh trong lớp không?

c) Có cách nào tính gần đúng thời gian tự học trung bình của các học sinh trong lớp dựa trên mẫu số liệu ghép nhóm này không?

Giải Toán 11 Bài 9: Các số đặc trưng đo xu thế trung tâm

Bài giảng Toán 11 Bài 9: Các số đặc trưng đo xu thế trung tâm

Giải Toán 11 trang 62

Mở đầu trang 62 Toán 11 Tập 1: Một cửa hàng đã ghi lại số tiền bán xăng cho 35 khách hàng đi xe máy. Mẫu số liệu gốc có dạng: x1, x2, ..., x35­ trong đó xi là số tiền bán xăng cho khách hàng thứ i. Vì một lí do nào đó, cửa hàng chỉ có mẫu số liệu ghép nhóm dạng sau:

Bảng 3.1. Số tiền khách hàng mua xăng

Dựa trên mẫu số liệu ghép nhóm này, làm thế nào để ước lượng các số đặc trưng đo xu thế trung tâm (số trung bình, trung vị, tứ phân vị, mốt) cho mẫu số liệu gốc?

Bài 3.3 trang 61 Toán 11 Tập 1: Thời gian ra sân (giờ) của một số cựu cầu thủ ở giải ngoại hạng Anh qua các thời kì được cho như sau:

Hãy chuyển mẫu số liệu trên sang dạng ghép nhóm với bảy nhóm có độ dài bằng nhau.

Bài 3.2 trang 61 Toán 11 Tập 1: Số sản phẩm một công nhân làm được trong một ngày được cho như sau:

Hãy chuyển mẫu số liệu sang dạng ghép nhóm với sáu nhóm có độ dài bằng nhau.

Bài tập

Bài 3.1 trang 61 Toán 11 Tập 1: Trong các mẫu số liệu sau, mẫu nào là mẫu số liệu ghép nhóm? Đọc và giải thích mẫu số liệu ghép nhóm đó.

a) Số tiền mà sinh viên chi cho thanh toán cước điện thoại trong tháng.

b) Thống kê nhiệt độ tại một địa điểm trong 40 ngày, ta có bảng số liệu sau:

Giải Toán 11 trang 61

Vận dụng trang 61 Toán 11 Tập 1: Một công ty may quần áo đồng phục học sinh cho biết cỡ áo theo chiều cao của học sinh được tính như sau:

Công ty muốn ước lượng tỉ lệ các cỡ áo khi may cho học sinh lớp 11 đã đo chiều cao của 36 học sinh nam khối 11 của một trường và thu được mẫu số liệu sau (đơn vị là centimét):

a) Lập bảng tần số ghép nhóm của mẫu số liệu với các nhóm đã cho ở bảng trên.

b) Công ty may 500 áo đồng phục cho học sinh lớp 11 thì nên may số lượng áo theo mỗi cỡ là bao nhiêu chiếc?

Luyện tập 2 trang 60 Toán 11 Tập 1: Cân nặng (kg) của 35 người trưởng thành tại một khu dân cư được cho như sau:

Chuyển mẫu số liệu trên thành dạng ghép nhóm, các nhóm có độ dài bằng nhau, trong đó có nhóm [40; 45).

2. Ghép nhóm mẫu số liệu

Giải Toán 11 trang 60

HĐ2 trang 60 Toán 11 Tập 1: Chỉ số BMI (đo bằng w/h2, trong đó w là cân nặng đơn vị kilôgam, h là chiều cao đơn vị là mét) của các học sinh trong một tổ được cho như sau:

Một người có chỉ số BMI nhỏ hơn 18,5 được xem là thiếu cân; từ 18,5 đến dưới 23 là có cân nặng lí tưởng so với chiều cao; từ 23 trở lên là thừa cân. Hãy lập mẫu số liệu ghép nhóm cho mẫu số liệu trên để biểu diễn tình trạng cân nặng so với chiều cao của các học sinh trong tổ.

Luyện tập 1 trang 59 Toán 11 Tập 1: Cho mẫu số liệu ghép nhóm về thời gian (phút) đi từ nhà đến nơi làm việc của các nhân viên một công ty như sau:

Đọc và giải thích mẫu số liệu này.

1. Giới thiệu về mẫu số liệu ghép nhóm

Giải Toán 11 trang 59

HĐ1 trang 59 Toán 11 Tập 1: Xét dữ liệu cho trong tình huống mở đầu.

a) Mẫu số liệu về tổng điểm, kí hiệu là (T), có bao nhiêu giá trị?

b) Nếu lập bảng tần số cho mẫu số liệu (T) thì có thể hình dung được bức tranh tổng thể về kết quả thi không? Vì sao?

c) Mẫu số liệu (T) được mô tả dưới dạng bảng thống kê sau:

Hãy đọc và giải thích số liệu được biểu diễn trong bảng thống kê.

Giải Toán 11 Bài 8: Mẫu số liệu ghép nhóm

Bài giảng Toán 11 Bài 8: Mẫu số liệu ghép nhóm

Giải Toán 11 trang 58

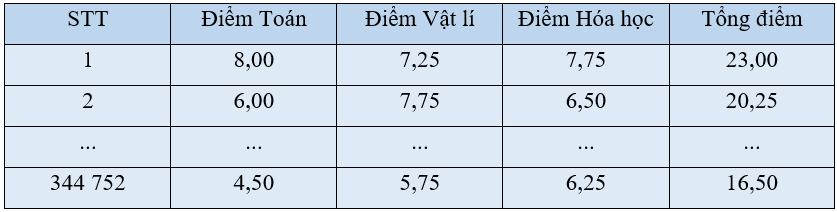
Mở đầu trang 58 Toán 11 Tập 1: Trong kì thi tốt nghiệp Trung học phổ thông năm 2021 đợt 1 có 344 752 thí sinh dự thi cả ba môn Toán, Vật lí, Hóa học (theo: vietnamnet.vn, ngày 26/07/2021). Giả sử điểm thi của các thí sinh này được cho trong bảng số liệu sau:

Các trường đại học, cao đẳng tuyển sinh theo tổ hợp A00 quan tâm đến tổng điểm ba môn của các thí sinh này. Biểu diễn dãy số liệu về tổng điểm ba môn của các thí sinh này thế nào để các trường thấy được bức tranh tổng thể về kết quả thi?

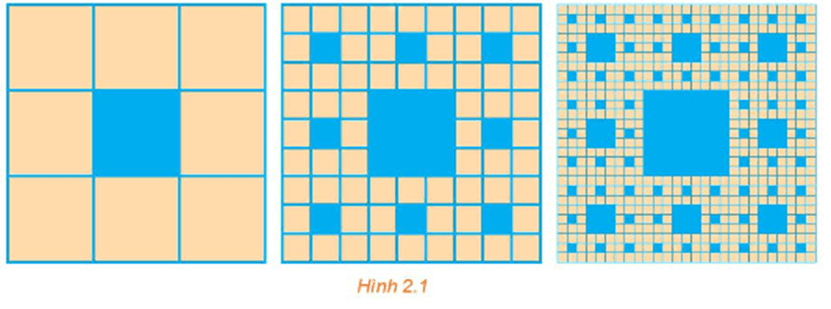
Bài 2.32 trang 57 Toán 11 Tập 1: Một hình vuông màu vàng có cạnh 1 đơn vị dài được chia thành chín hình vuông nhỏ hơn và hình vuông ở chính giữa được tô màu xanh như Hình 2.1. Mỗi hình vuông màu vàng nhỏ hơn lại được chia thành chín hình vuông con, và mỗi hình vuông con ở chính giữa là được tô màu xanh. Nếu quá trình này được tiếp tục lặp lại năm lần, thì tổng diện tích các hình vuông được tô màu xanh bằng bao nhiêu?

Bài 2.31 trang 57 Toán 11 Tập 1: Mặt sàn tầng một (tầng trệt) của một ngôi nhà cao hơn mặt sân 0,5 m. Cầu thang đi từ tầng một lên tầng hai gồm 25 bậc, mỗi bậc cao 16 cm.

a) Viết công thức để tìm độ cao của bậc cầu thang thứ n so với mặt sân.

b) Tính độ cao của sàn tầng hai so với mặt sân.

Bài 2.30 trang 57 Toán 11 Tập 1: Tìm ba số, biết theo thứ tự chúng lập thành cấp số cộng và có tổng bằng 21, và nếu lần lượt cộng thêm các số 2; 3; 9 vào ba số đó thì được ba số lập thành một cấp số nhân.

Bài 2.29 trang 57 Toán 11 Tập 1: Chứng minh rằng:

a) Trong một cấp số cộng (un), mỗi số hạng (trừ số hạng đầu và số hạng cuối, nếu có) đều là trung bình cộng của hai số hạng đứng kề với nó, nghĩa là

$u_k=\frac{u_{k-1}+u_{k+1}}{2}$ với k ≥ 2.

b) Trong một cấp số nhân, bình phương của mỗi số hạng (trừ số hạng đầu và số hạng cuối, nếu có) đều là tích của hai số hạng đứng kề với nó, nghĩa là

$u_k^2=u_{k-1}.u_{k+1}$ với k ≥ 2.

Bài 2.28 trang 57 Toán 11 Tập 1: Tế bào E. Coli trong điều kiện nuôi cấy thích hợp cứ 20 phút lại phân đôi một lần. Hỏi sau 24 giờ, tế bào ban đầu sẽ phân chia thành bao nhiêu tế bào?

B. Tự luận

Giải Toán 11 trang 57

Bài 2.27 trang 57 Toán 11 Tập 1: Từ 0 giờ đến 12 giờ trưa, chuông của một chiếc đồng hồ quả lắc sẽ đánh bao nhiêu tiếng, biết rằng nó chỉ đánh chuông báo giờ và số tiếng chuông bằng số giờ?

Bài 2.26 trang 56 Toán 11 Tập 1: Tổng 100 số hạng đầu của dãy số (un) với u­n = 2n – 1 là

A. 199.

B. 2100 – 1.

C. 10 000.

D. 9 999.

Bài 2.25 trang 56 Toán 11 Tập 1: Trong các dãy số cho bởi công thức truy hồi sau, dãy số nào là cấp số nhân?

A. u1 = – 1, $u_{n+1}=u_n^2$.

B. u1 = – 1, un + 1 = 2un.

C. u1 = – 1, un + 1 = un + 2.

D. u1 = – 1, un + 1 = u­n – 2.

Bài 2.24 trang 56 Toán 11 Tập 1: Cho dãy số (un) với un = 3n + 6. Khẳng định nào sau đây là đúng?

A. Dãy số (un) là cấp số cộng với công sai d = 3.

B. Dãy số (un) là cấp số cộng với công sai d = 6.

C. Dãy số (un) là cấp số nhân với công bội q = 3.

D. Dãy số (un) là cấp số nhân với công bội q = 6.

Bài 2.23 trang 56 Toán 11 Tập 1: Cho dãy số

1, $\frac{1}{2},\frac{1}{4},\frac{1}{8},\mathrm{...}$ (số hạng sau bằng một nửa số hạng liền trước nó).

Công thức tổng quát của dãy số đã cho là

A. $u_n={\left(\frac{1}{2}\right)}^n$ .

B. $u_n=\frac{{\left(-1\right)}^n}{2^{n-1}}$ .

C. $u_n=\frac{1}{2n}$ .

D. $u_n={\left(\frac{1}{2}\right)}^{n-1}$ .

Giải Toán 11 Bài tập cuối chương 2

Bài giảng Toán 11 Bài tập cuối chương 2

A. Trắc nghiệm

Giải Toán 11 trang 56

Bài 2.22 trang 56 Toán 11 Tập 1: Khẳng định nào sau đây là sai?

A. Một dãy số tăng thì bị chặn dưới.

B. Một dãy số giảm thì bị chặn trên.

C. Một dãy số bị chặn thì phải tăng hoặc giảm.

D. Một dãy số không đổi thì bị chặn.

Bài 2.21 trang 55 Toán 11 Tập 1: Một loại thuốc được dùng mỗi ngày một lần. Lúc đầu nồng độ thuốc trong máu của bệnh nhân tăng nhanh, nhưng mỗi liều tiếp có tác dụng ít hơn liều trước đó. Lượng thuốc trong máu ở ngày thứ nhất là 50 mg, và mỗi ngày sau đó giảm chỉ còn một nửa so với ngày kề trước đó. Tính tổng lượng thuốc (tính bằng mg) trong máu của bệnh nhân sau khi dùng thuốc 10 ngày liên tiếp.

Bài 2.20 trang 55 Toán 11 Tập 1: Vào năm 2020, dân số của một quốc gia là khoảng 97 triệu người và tốc độ tăng trưởng dân số là 0,91%. Nếu tốc độ tăng trưởng dân số này được giữ nguyên hằng năm, hãy ước tính dân số của quốc gia đó vào năm 2030.

Bài 2.19 trang 55 Toán 11 Tập 1: Một công ty xây dựng mua một chiếc máy ủi với giá 3 tỉ đồng. Cứ sau mỗi năm sử dụng, giá trị của chiếc máy ủi này lại giảm 20% so với giá trị của nó trong năm liền trước đó. Tìm giá trị còn lại của chiếc máy ủi đó sau 5 năm sử dụng.

Bài 2.18 trang 55 Toán 11 Tập 1: Một cấp số nhân có số hạng đầu bằng 5 và công bội bằng 2. Hỏi phải lấy tổng của bao nhiêu số hạng đầu của cấp số nhân này để có tổng bằng 5115?

Bài 2.17 trang 55 Toán 11 Tập 1: Một cấp số nhân có số hạng thứ 6 bằng 96 và số hạng thứ 3 bằng 12. Tìm số hạng thứ 50 của cấp số nhân này.

Bài 2.16 trang 55 Toán 11 Tập 1: Viết năm số hạng đầu của mỗi dãy số (un) sau và xem nó có phải là cấp số nhân không. Nếu nó là cấp số nhân, hãy tìm công bội q và viết công thức tính số hạng tổng quát của nó dưới dạng un = u1 . qn – 1.

a) un = 5n;

b) un = 5n;

c) u1 = 1, un = nun – 1;

d) u1 = 1, un = 5un – 1.

Bài tập

Bài 2.15 trang 55 Toán 11 Tập 1: Xác định công bội, số hạng thứ 5, số hạng tổng quát và số hạng thứ 100 của mỗi cấp số nhân sau:

a) 1, 4, 16, ...;

b) 2, $-\frac{1}{2},\frac{1}{8}$ , ....