Đường cong nào sau đây là đồ thị của hàm số $y = \frac{1 - x}{x + 1}$?

A. 

B. 

C. 

D. 

Đường cong ở Hình 29 là đồ thị của hàm số:

A. y = x3 + x2 + 2x + 2.

B. y = – x3 – 4x2 – x + 2.

C. y = x3 + 3x2 – 4x + 2.

D. y = x3 + 3x2 + 4x + 2.

Đồ thị hàm số y = x3 – 3x – 1 là đường cong nào trong các đường cong sau?

A. 

B. 

C. 

D. 

Trong Ví dụ 9, góc dốc của con đường trên đoạn [– 1 000; 1 000] lớn nhất tại điểm nào?

Khảo sát sự biến thiên và vẽ đồ thị hàm số $y = \frac{x^2+ x - 3}{x + 1}$.

Khảo sát sự biến thiên và vẽ đồ thị hàm số $y = \frac{-x^2}{x + 1}$.

Khảo sát sự biến thiên và vẽ đồ thị hàm số $y = \frac{x - 3}{-x + 2}$

Khảo sát sự biến thiên và vẽ đồ thị hàm số $y = \frac{2x + 6}{-x + 2}$

Khảo sát sự biến thiên và vẽ đồ thị của mỗi hàm số sau:

a) y = – x3 + 3x – 2;

b) y = x3 + 3x2 + 3x + 1.

Khảo sát sự biến thiên và vẽ đồ thị của hàm số $y = \frac{x - 1}{x + 1}$

Lập bảng biến thiên và vẽ đồ thị của hàm số y = x2 – 2x – 3.

Trong 20 phút theo dõi, lưu lượng nước của một con sông được tính theo công thức

Q(t) = $-\frac{1}{5}{t}^3 + 5t^2+ 100$,

trong đó Q được tính theo m3/phút, t tính theo phút, 0 ≤ t ≤ 20 (Nguồn: A. Bigalke et al., Mathematik, Grundkurs ma-1, Cornelsen 2016). Khi lưu lượng nước của con sông lên đến 550 m3/phút thì cảnh báo lũ được đưa ra.

Trong thời gian theo dõi, lưu lượng nước của con sông lớn nhất là bao nhiêu? Cảnh báo lũ được đưa ra vào thời điểm nào?

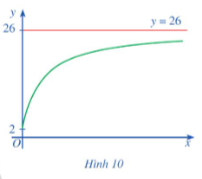
Số lượng sản phẩm bán được cho một công ty trong x (tháng) được tính theo công thức

$S\left(x\right)=200\left(5-\frac{9}{2+x}\right)$ trong đó $x\ge 1$.

a) Xem $y=S\left(x\right)$ là một hàm số xác định trên nửa khoảng $[1;+\mathrm{\infty })$, hãy tìm tiệm cận ngang của đồ thị hàm số đó.

b) Nêu nhận xét về số lượng sản phẩm bán được của công ty đó trong x (tháng) khi x đủ lớn.

Tìm tiệm cận đứng, ngang, xiên (nếu có) của đồ thị mỗi hàm số sau:

a) $y=\frac{x}{2-x}$

b) $y=\frac{2x^2-3x+2}{x-1}$

c) $y=x-3+\frac{1}{x^2}$

Đồ thị hàm số ở Hình 18a, Hình 18b đều có đường tiệm cận ngang là đường thẳng màu đỏ. Hỏi đó là đồ thị của hàm số nào trong các hàm số sau đây?

a) $y=\frac{x^2+2x-1}{x^2+1}$.

b) $y=\frac{2x^2+x+1}{x-1}$

c) $y=\frac{2x^2-2}{x^2+2}$

Tiệm cận xiên của đồ thị hàm số $y=\frac{x^2+3x+5}{x+2}$ là:

A. $y=x$.

B. $y=x+1$.

C. $y=x+2$.

D. $y=x+3$.

Tiệm cận đứng của đồ thị hàm số $y=\frac{x+2}{x+1}$ là:

A. $x=-1$.

B. $x=-2$.

C. $x=1$.

D. $x=2$.

Tìm tiệm cận xiên của đồ thị hàm số $y=f\left(x\right)=\frac{x^2-3x+2}{x+3}$.

Chứng minh rằng đường thẳng $y=-x$ là tiệm cận xiên của đồ thị hàm số $y=f\left(x\right)=\frac{-x^2-2x+3}{x+2}$.

Cho hàm số $y=f\left(x\right)=x+1+\frac{1}{x-1}$ có đồ thị $\left(C\right)$ và đường thẳng $y=x+1$ (Hình 15). Tìm $\underset{x\to +\mathrm{\infty }}{lim}\left[f\left(x\right)-\left(x+1\right)\right];\underset{x\to -\mathrm{\infty }}{lim}\left[f\left(x\right)-\left(x+1\right)\right]$

Tìm tiệm cận đứng của đồ thị hàm số $y=\frac{x^2+3x}{x-5}$.

Cho hàm số $y=f\left(x\right)=\frac{1}{x}$ có đồ thị là đường cong như Hình 12. Tìm $\underset{x\to 0^{+}}{lim}f\left(x\right),\underset{x\to 0^{-}}{lim}f\left(x\right)$

Tìm tiệm cận ngang của đồ thị hàm số $y=\frac{3x-2}{x+1}$.

Xét hàm số $y=f\left(x\right)=\frac{26x+10}{x+5}$ với $x\in [0;+\mathrm{\infty })$ có đồ thị là đường cong ở Hình 10 trong bài toán mở đầu. Tìm $\underset{x\to +\mathrm{\infty }}{lim}f\left(x\right)$.

Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số $f\left(x\right)=\sin 2x-2x$ trên đoạn $\left[\frac{\pi }{2};\frac{3\pi }{2}\right]$.

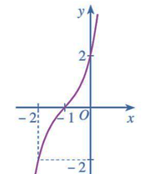
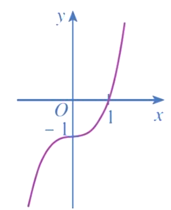
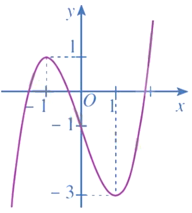
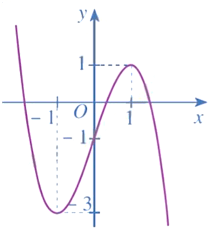
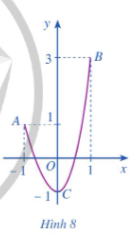
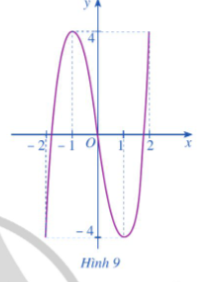
Cho hàm số $y=f\left(x\right)=2x^3-6x,x\in \left[-2;2\right]$ có đồ thị là đường cong ở Hình 9.

a) Dựa vào đồ thị ở Hình 9, hãy cho biết các giá trị $M=\underset{\left[-2;2\right]}{max}f\left(x\right);m=\underset{\left[-2;2\right]}{min}f\left(x\right)$ bằng bao nhiêu.

b) Giải phương trình $f^{\prime }\left(x\right)=0$ với $x\in \left(-2;2\right)$

c) Tính các giá trị của hàm số $f\left(x\right)$ tại hai đầu mút $-2;2$ và tại các điểm $x\in \left(-2;2\right)$ mà ở đó $f^{\prime }\left(x\right)=0$

d) So sánh M (hoặc m) với số lớn nhất (hoặc số bé nhất) trong các giá trị tính được ở câu c

Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của hàm số $y=\frac{2x-5}{x-1}$ trên nửa khoảng $(1;3]$.

Cho hàm số $f\left(x\right)=x+\frac{1}{x-1}$ với $x>1$.

a) Tính $\underset{x\to 1^{+}}{lim}f\left(x\right),\underset{x\to +\mathrm{\infty }}{lim}f\left(x\right)$.

b) Lập bảng biến thiên của hàm số $f\left(x\right)$ trên khoảng $\left(1;+\mathrm{\infty }\right)$.

c) Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của hàm số $f\left(x\right)$ trên khoảng $\left(1;+\mathrm{\infty }\right)$.

Tìm giá trị lớn nhất và nhỏ nhất của hàm số $f\left(x\right)=\sqrt{9-x^2}$ trên đoạn $\left[-3;3\right]$.

Cho hàm số $y=f\left(x\right)$ liên tục trên đoạn $\left[-1;1\right]$ và có đồ thị là đường cong ở Hình 8. Quan sát đồ thị và cho biết:

a) Điểm nào thuộc đồ thị hàm số có tung độ lớn nhất

b) Điểm nào thuộc đồ thị hàm số có tung độ nhỏ nhất

Kính viễn vọng không gian Hubble được đưa vào vũ trụ ngày 24/4/1990 bằng tàu con thoi Discovery. Vận tốc của tàu con thoi trong sứ mệnh này, từ lúc cất cánh tại thời điểm $t=0\left(s\right)$ cho đến khi tên lửa đẩy được phóng đi tại thời điểm $t=126\left(s\right)$, cho bởi hàm số sau:

$v\left(t\right)=0,001320t^3-0,09029t^2+23$.

(v được tính bằng ft/s, 1 feet = 0,3048 m)

Hỏi gia tốc của tàu con thoi sẽ tăng trong khoảng thời gian nào tính từ thời điểm cất cánh cho đến khi tên lửa đẩy được phóng đi?

Thể tích V (đơn vị: centimet khối) của 1kg nước tại nhiệt độ T được tính bởi công thức sau:

Hỏi thể tích , giảm trong khoảng nhiệt độ nào?

Cho hai hàm số $y=f\left(x\right),y=g\left(x\right)$ có đồ thị hàm số lần lượt ở Hình 6a, Hình 6b. Nêu khoảng đồng biến, nghịch biến và điểm cực trị của mỗi hàm số đó.

Tìm cực trị của mỗi hàm số sau:

a) $y=2x^3+3x^2-36x-10$

b) $y=x^4+2x^2-3$

c) $y=x-\frac{1}{x}$

Tìm các khoảng đơn điệu của hàm số sau:

a) $y=-x^3+2x^2-3$ b) $y=x^4-2x^2+5$

c) $y=\frac{3x+1}{2-x}$ d) $y=\frac{x^2-2x}{x+1}$

Cho hàm số $y=f\left(x\right)$có bảng biến thiên như sau:

Giá trị cực tiểu của hàm số đã cho bằng:

a) $2$.

b) $3$.

c) $-4$.

d) $0$.

Cho hàm số $y=f\left(x\right)$có bảng biến thiên như sau:

Hàm số đồng biến trên khoảng nào dưới đây?

A. $\left(1;+\mathrm{\infty }\right)$.

B. $\left(-1;0\right)$.

C. $\left(-1;1\right)$.

D. $\left(0;1\right)$.

Tìm điểm cực trị của mỗi hàm số sau:

a) $y=x^4-6x^2+8x+1$.

b) $y=\frac{3x+5}{x-1}$.

Quan sát bảng biến thiên dưới đây và cho biết:

a) $x_o$ có là điểm cực đại của hàm số $f\left(x\right)$ hay không.

b) $x_1$ có là điểm cực tiểu của hàm số $h\left(x\right)$ hay không.

Dựa vào đồ thị hàm số $y=f\left(x\right)=-x^3-3x^2+3$ ở Hình 3, hãy so sánh:

a) $f\left(-2\right)$ với mỗi giá trị $f\left(x\right)$, ở đó $x\in \left(-3;-1\right)$ và $x\ne -2$.

b) $f\left(0\right)$với mỗi giá trị $f\left(x\right)$, ở đó $x\in \left(-1;1\right)$ và $x\ne 0$.