Tìm số nguyên để đạt giá trị nhỏ nhất.
Hướng dẫn giải:
Với mọi số nguyên x thì A luôn xác định.
Ta có:
đạt giá trị nhỏ nhất khi và chỉ khi đạt giá trị nhỏ nhất hay đạt giá trị lớn nhất.
Từ đó lí luận chỉ ra được .
Do đó (thỏa mãn). Khi đó .
Suy ra min đạt được tại .
Vậy thì đạt giá trị nhỏ nhất.
Đề thi học kì 1 Toán 7 KNTT có đáp án - Đề 3
Cho tam giác có . Gọi là trung điểm của .
a) Chứng minh: ;
b) Kẻ đường thẳng qua và vuông góc với tại . Trên tia đối của tia lấy điểm sao cho . Chứng minh: ;
c) Kẻ vuông góc với tại , cắt cạnh tại . Chứng minh: .
Hướng dẫn giải:
a)
Xét và có:
(gt)
(cạnh chung)
(gt)
Suy ra (c.c.c)
b)
Xét và có:
(gt)
( đồng vị)
(gt)
Do đó (c.g.c)
Suy ra ( hai góc tương ứng) (1)
Mà hai góc này ở vị trí so le trong
Nên .
c)
Ta có (theo câu a)
Suy ra ( hai góc tương ứng) (2)
Và ( hai cạnh tương ứng) (3)
Từ (1) và (2) suy ra
Từ đó chứng minh được (g.c.g)
Suy ra ( hai cạnh tương ứng) (4)
Mà (hai cạnh tương ứng của ) suy ra (5)
Từ (3) và (5) chỉ ra được
Suy ra tam giác cân tại (*)
Ta có nên tam giác cân tại
(**)
Từ (*) và (**) suy ra
Mà mà hai góc này ở vị trí đồng vị nên
Dễ chỉ ra được vuông góc với .
Do đó vuông góc với .
Đề thi học kì 1 Toán 7 KNTT có đáp án - Đề 3
Khẳng định nào sau đây là đúng?
Đề thi học kì 1 Toán 7 KNTT có đáp án - Đề 3
Biểu đồ Hình 3 dưới đây cho biết số người được tiêm Vaccine Covid mũi ở Việt Nam từ tháng đến tháng . Quan sát biểu đồ và trả lời câu 11, câu 12.
Từ tháng 3 đến tháng 6 năm 2021, tháng có số người được tiêm vaccine Covid 19 mũi 1 nhiều nhất là
Đề thi học kì 1 Toán 7 KNTT có đáp án - Đề 3
Cho hình vẽ biết , và vuông góc với nhau,
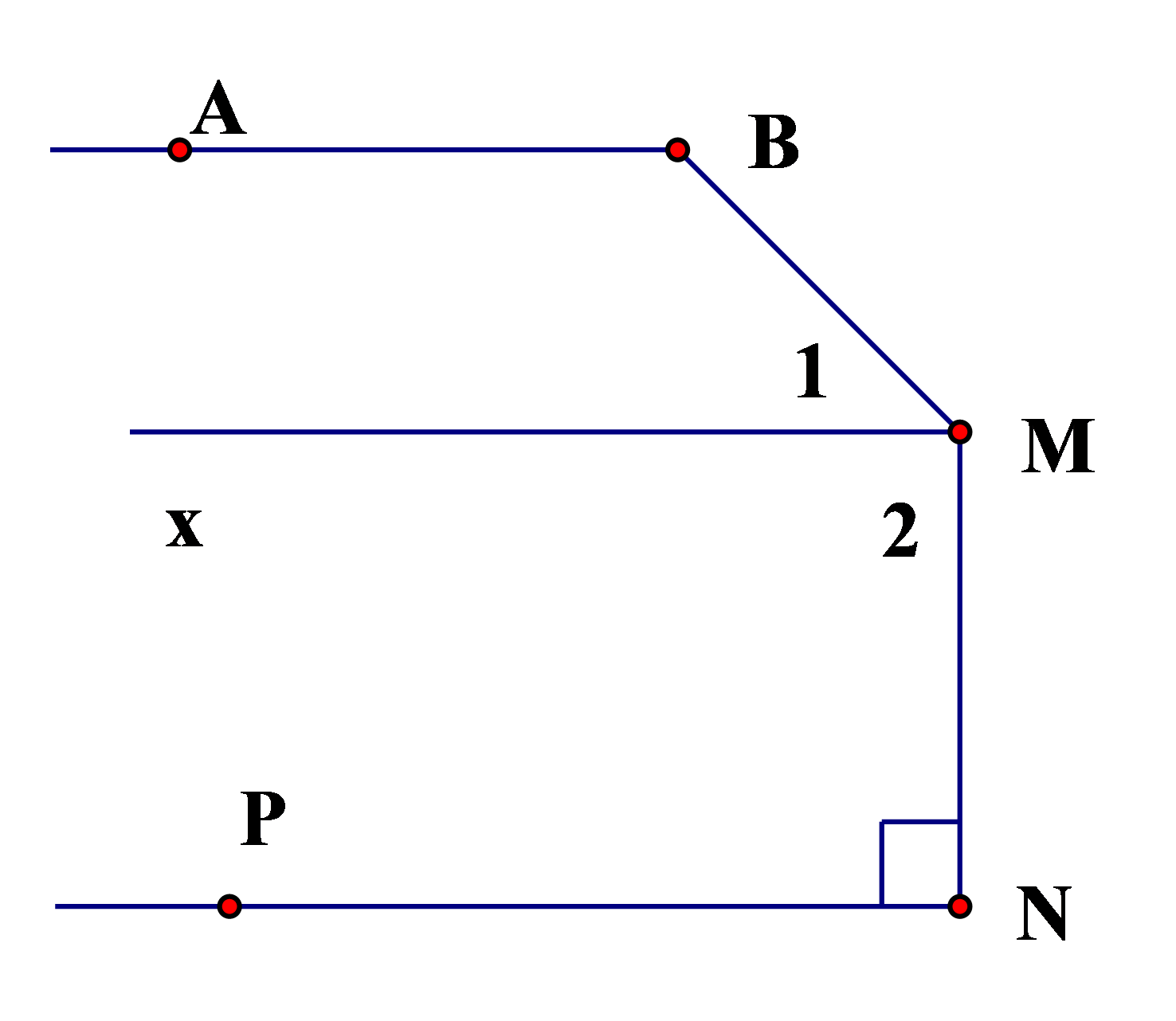
1) Tính số đo các góc .
2) Chứng minh: .
3) Kẻ tia phân giác của , cắt tia tại điểm . Chứng minh: .
Hướng dẫn giải:
GT, KL: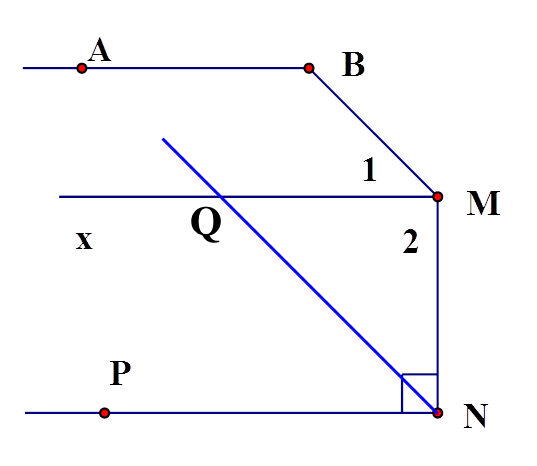
Để làm ý 1,2 HS không cần thiết phải vẽ hình
1) Ta có: Þ
Hay Þ
Vì ÞÞ
2) Vì Þ
Mà (gt)
Nên (vì cùng vuông góc với )
Do đó (vì cùng song song với ).
3) Vì MQ là tia phân giác của
Þ Þ
Vì Þ (cặp góc so le trong)
Þ Þ (đpcm)
Đề thi học kì 1 Toán 7 KNTT có đáp án - Đề 2
Tùng, Huy và Minh cùng trồng hoa cúc trong chậu để bán dịp tết. Tùng trồng được 6 chậu hoa, Huy trồng được 4 chậu hoa và Minh trồng được 5 chậu hoa. Ba bạn bán hết hoa thu được tổng số tiền là 1,5 triệu đồng. Ba bạn quyết định chia tiền tỉ lệ với số chậu hoa trồng được. Tính số tiền mỗi bạn nhận được?
Hướng dẫn giải:
Gọi số tiền ba bạn Tùng, Huy và Minh nhận được lần lượt là (triệu đồng)
Vì tổng số tiền ba bạn nhận được khi bán hết chậu hoa là triệu đồng nên ta có: .
Vì số tiền mỗi bạn nhận được tỉ lệ với số chậu hoa trồng được nên ta có: .
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
Suy ra:
(thỏa mãn)
Vậy số tiền bạn Tùng, Huy và Minh nhận được lần lượt là: 0,6 triệu đồng, 0,4 triệu đồng, 0,5 triệu đồng.
Đề thi học kì 1 Toán 7 KNTT có đáp án - Đề 2