Câu hỏi:
85 lượt xemGiả sử ĐO là phép đối xứng tâm O. Lấy hai điểm tùy ý A, B sao cho ba điểm O, A, B không thẳng hàng. Gọi A’, B’ lần lượt là ảnh của A, B qua ĐO. So sánh tam giác OAB và tam giác O’A’B’ rồi so sánh A’B’ và AB.
Lời giải
Hướng dẫn giải:
Theo đề, ta có ĐO(A) = A’.
Suy ra O là trung điểm AA’, do đó OA = OA’.
Chứng minh tương tự, ta được OB = OB’.
Xét ∆OAB và ∆OA’B’, có:
OA = OA’ (chứng minh trên);
(đối đỉnh);
OB = OB’ (chứng minh trên).
Do đó ∆OAB = ∆OA’B’ (c.g.c).
Suy ra AB = A’B’ (cặp cạnh tương ứng).
Vậy ∆OAB = ∆OA’B’ và A’B’ = AB.
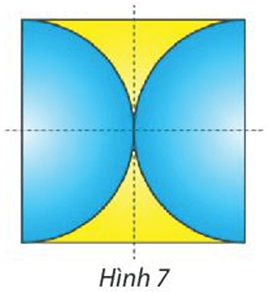
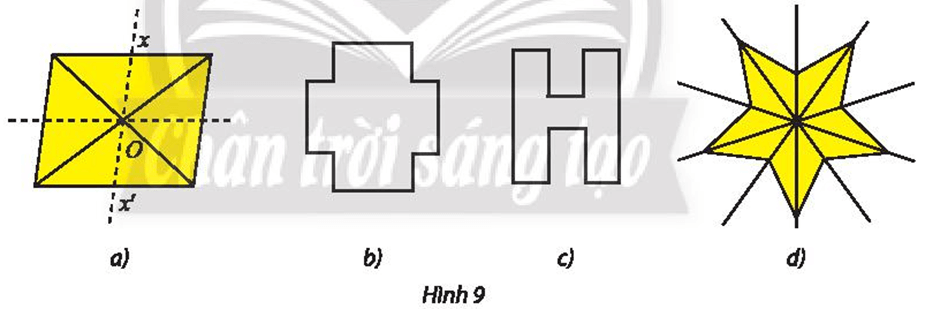
Tìm phép đối xứng trục và phép đối xứng tâm biến Hình 7 thành chính nó.
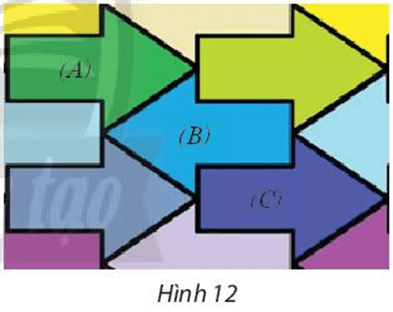
Trong Hình 11, hình nào có trục đối xứng, hình nào có tâm đối xứng?