Câu hỏi:
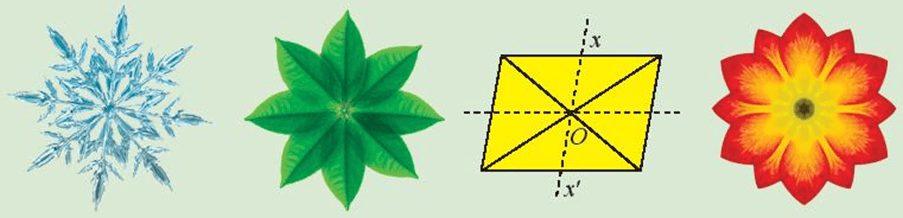
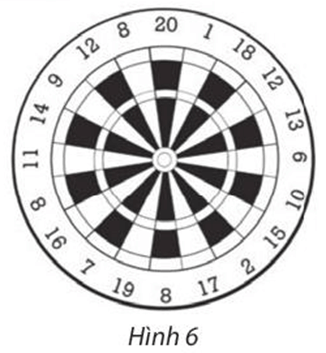
111 lượt xemTrong các hình sau, hình nào có tâm đối xứng?
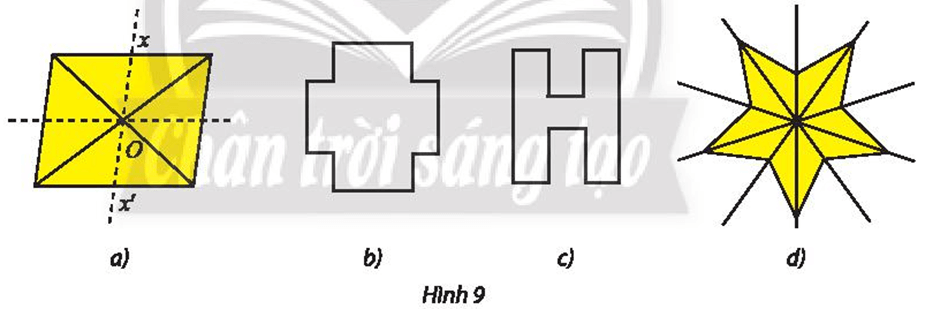
Tồn tại hay không phép biến hình biến mỗi hình phẳng sau đây thành chính nó?
Lời giải
Hướng dẫn giải:
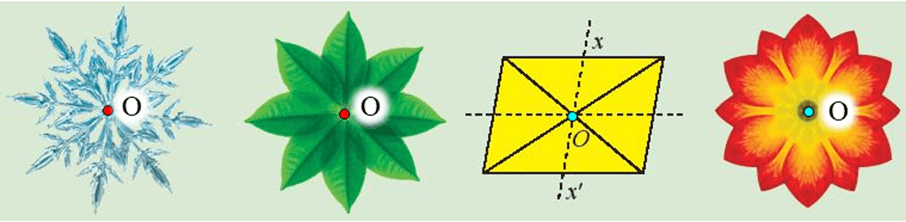
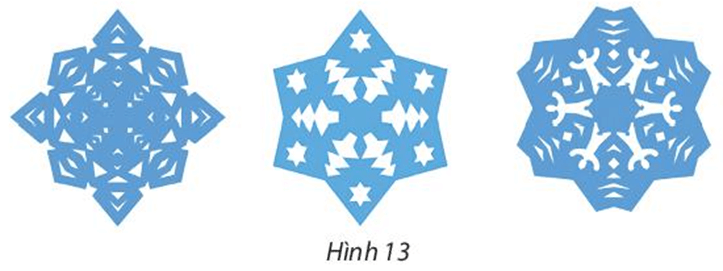
⦁ Cả 4 hình đều có tâm đối xứng là điểm O như hình vẽ dưới đây:
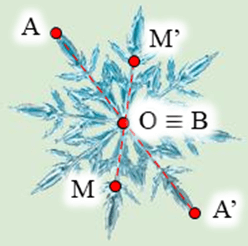
⦁ Ta xét hình bông tuyết:
Lấy điểm B trùng O. Khi đó qua O, điểm đối xứng với B là chính nó.
Lấy điểm A bất kì trên hình bông tuyết sao cho A ≠ O.
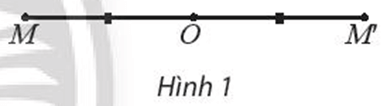
Khi đó ta luôn xác định được một điểm A’ sao cho O là trung điểm của đoạn AA’.
Tương tự như vậy, mỗi điểm M bất kì khác O trên hình bông tuyết, ta đều xác định được một điểm M’ trên hình sao cho O là trung điểm của đoạn MM’.
Vì vậy phép biến hình biến hình bông tuyết thành chính nó là phép biến hình biến hình biến điểm O thành chính nó và biến mỗi điểm M khác O thành điểm M’ sao cho O là trung điểm của đoạn MM’.
Chứng minh tương tự với hình 8 chiếc lá, hình bình hành và hình bông hoa, ta cũng được kết quả như trên.
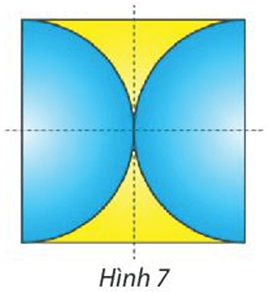
Tìm phép đối xứng trục và phép đối xứng tâm biến Hình 7 thành chính nó.
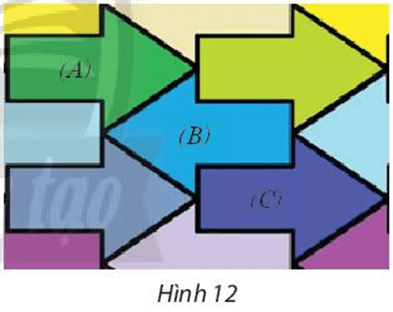
Trong Hình 11, hình nào có trục đối xứng, hình nào có tâm đối xứng?