Câu hỏi:
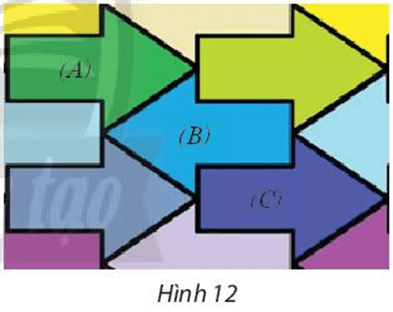
102 lượt xemTrong Hình 12, tìm phép đối xứng biến hình mũi tên (A) thành hình mũi tên (B) và tìm phép đối xứng biến hình mũi tên (B) thành hình mũi tên (C).
Lời giải
Hướng dẫn giải:
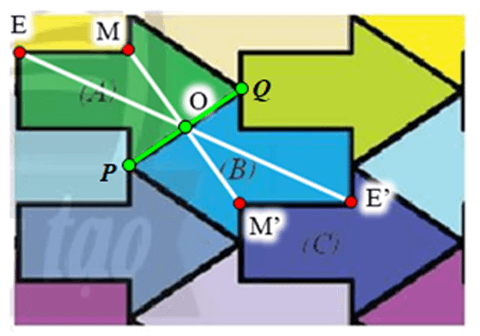
⦁ Gọi P, Q là hai điểm nằm trên cạnh của mũi tên (A) như hình vẽ.
Lấy O là trung điểm của PQ.
Gọi E là một điểm trên hình mũi tên (A).
Lấy điểm E’ là ảnh của E qua ĐO.
Khi đó O là trung điểm của EE’, E’ một điểm trên hình mũi tên (B) có vị trí tương ứng với điểm E trên hình mũi tên (A).
Tương tự như vậy, với mỗi điểm M bất kì trên hình mũi tên (A), ta lấy điểm M’ là ảnh của M qua ĐO thì ta được tập hợp các điểm M’ tạo thành hình mũi tên (B).
Vậy phép đối xứng tâm O biến hình mũi tên (A) thành hình mũi tên (B), với O là trung điểm của PQ trên hình mũi tên (A) (như hình vẽ).
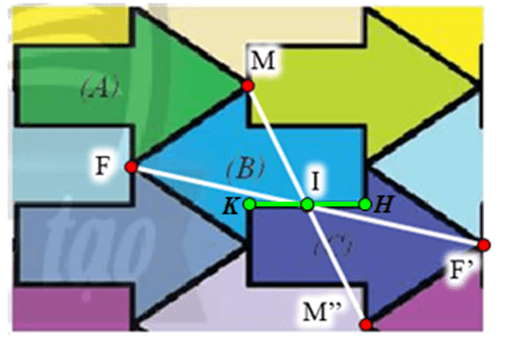
⦁ Gọi H, K là hai điểm nằm trên cạnh của mũi tên (B) như hình vẽ.
Lấy I là trung điểm của HK.
Chứng minh tương tự như trên, ta thu được phép đối xứng tâm I biến hình mũi tên (B) thành hình mũi tên (C), với I là trung điểm của HK trên hình mũi tên (B) (như hình vẽ).
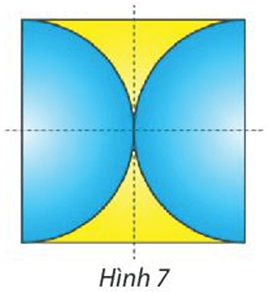
Tìm phép đối xứng trục và phép đối xứng tâm biến Hình 7 thành chính nó.
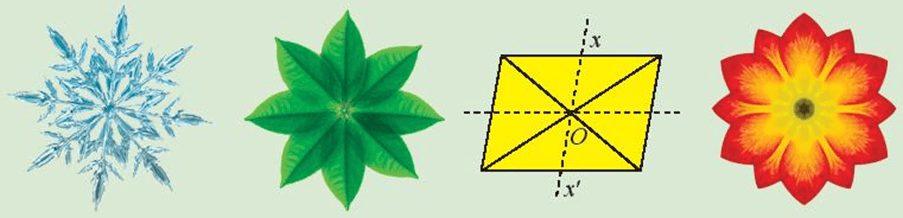
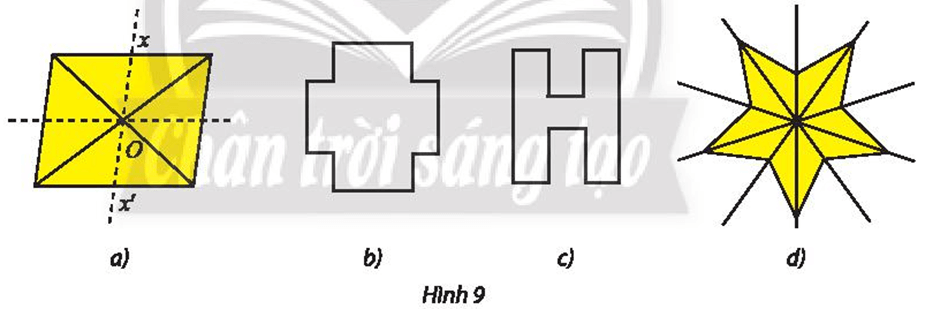
Trong Hình 11, hình nào có trục đối xứng, hình nào có tâm đối xứng?