Lý thuyết Giới hạn của hàm số (Cánh diều 2024) Toán 11

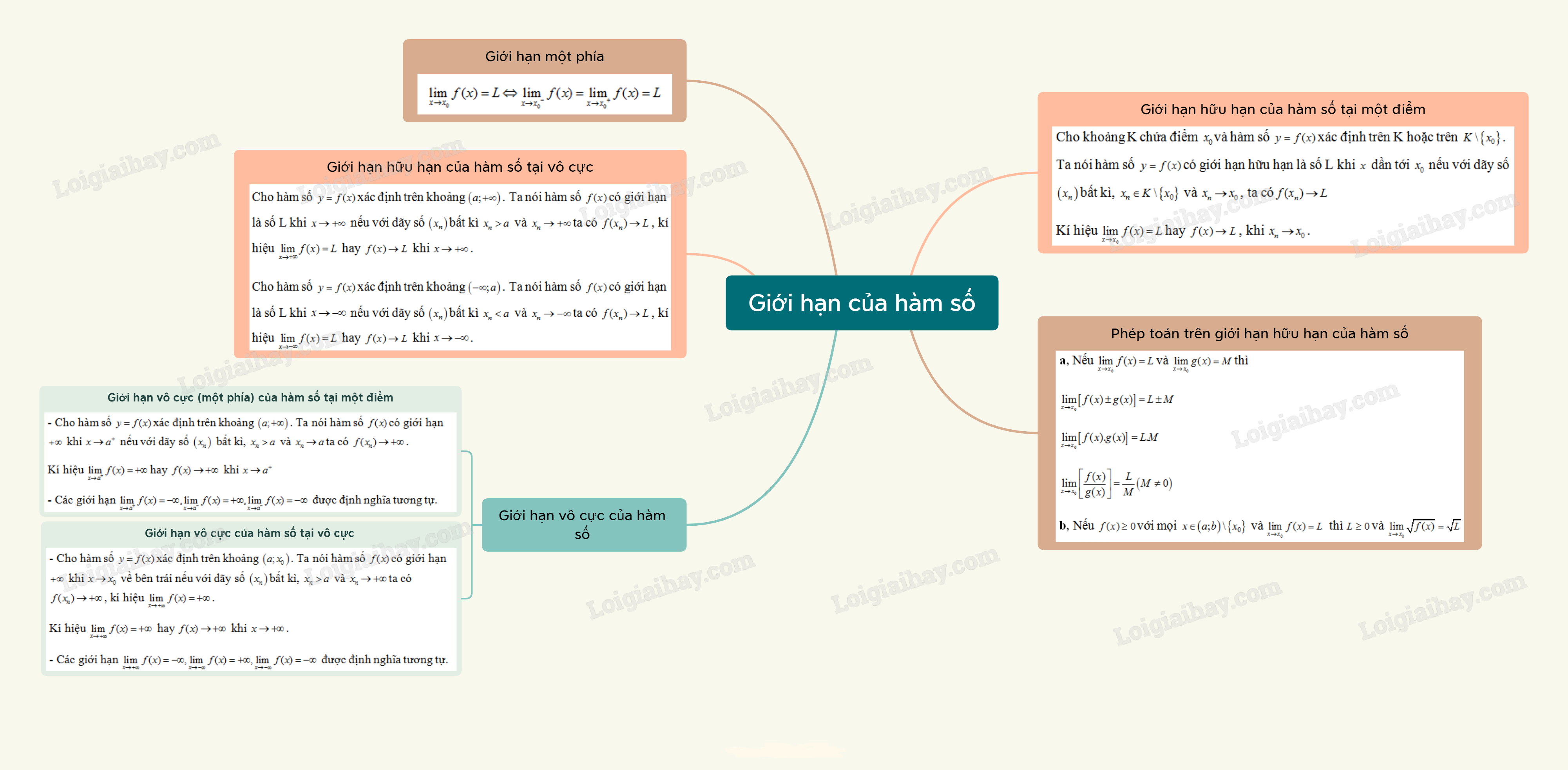
I. Giới hạn hữu hạn của hàm số tại một điểm

1. Định nghĩa

Cho khoảng K chứa điểm $x_0$và hàm số $f(x)$ xác định trên K hoặc trên $K\mathrm{\setminus }\left\{x_0\right\}$. Hàm số $f(x)$có giới hạn là số L khi $x$ dần tới $x_0$ nếu với dãy số $\left(x_n\right)$bất kì, $x_n\in K\mathrm{\setminus }\left\{x_0\right\}$ và $x_n\to x_0$, ta có$f(x_n)\to L$

Kí hiệu $\underset{x\to x_0}{lim}f(x)=L$ hay $f(x)\to L$, khi $x_n\to x_0$.

2. Phép toán trên giới hạn hữu hạn của hàm số

a, Nếu $\underset{x\to x_0}{lim}f(x)=L$ và $\underset{x\to x_0}{lim}g(x)=M$$\left(L,M\in \mathbb{R}\right)$thì

$\underset{x\to x_0}{lim}\left[f(x)\pm g(x)\right]=L\pm M$

$\underset{x\to x_0}{lim}\left[f(x).g(x)\right]=L.M$

$\underset{x\to x_0}{lim}\left[\frac{f(x)}{g(x)}\right]=\frac{L}{M}\left(M\ne 0\right)$

b, Nếu $f(x)\ge 0$ với mọi $x\in \left(a;b\right)\mathrm{\setminus }\left\{x_0\right\}$ và $\underset{x\to x_0}{lim}f(x)=L$ thì $L\ge 0$ và $\underset{x\to x_0}{lim}\sqrt{f(x)}=\sqrt{L}$.

3. Giới hạn một phía

- Cho hàm số $y=f(x)$ xác định trên khoảng $\left(a;x_0\right)$. Số L được gọi là giới hạn bên trái của hàm số $y=f(x)$ khi $x\to x_0$ nếu với dãy số $\left(x_n\right)$ bất kì thỏa mãn $a<x_n<x_0$ và $x_n\to x_0$ ta có $f(x_n)\to L$, kí hiệu $\underset{x\to {x_0}^{-}}{lim}f(x)=L$.

- Cho hàm số $y=f(x)$ xác định trên khoảng $\left(x_0;b\right)$. Số L là giới hạn bên của hàm số $y=f(x)$ khi $x\to x_0$ nếu với dãy số $\left(x_n\right)$bất kì thỏa mãn $x_0<x_n<b$ và $x_n\to x_0$ ta có $f(x_n)\to L$, kí hiệu $\underset{x\to {x_0}^{+}}{lim}f(x)=L$.

*Nhận xét: $\underset{x\to x_0}{lim}f(x)=L\iff \underset{x\to {x_0}^{-}}{lim}f(x)=\underset{x\to {x_0}^{+}}{lim}f(x)=L$

II. Giới hạn hữu hạn của hàm số tại vô cực

- Cho hàm số $y=f(x)$xác định trên khoảng $\left(a;+\mathrm{\infty }\right)$. Ta nói hàm số $f(x)$ có giới hạn là số L khi $x\to +\mathrm{\infty }$ nếu với dãy số $\left(x_n\right)$bất kì $x_n>a$ và $x_n\to +\mathrm{\infty }$ta có $f(x_n)\to L$, kí hiệu $\underset{x\to +\mathrm{\infty }}{lim}f(x)=L$ hay $f(x)\to L$ khi $x\to +\mathrm{\infty }$.

- Cho hàm số $y=f(x)$ xác định trên khoảng $\left(-\mathrm{\infty };b\right)$. Ta nói hàm số $f(x)$ có giới hạn là số L khi $x\to -\mathrm{\infty }$ nếu với dãy số $\left(x_n\right)$bất kì $x_n<b$ và $x_n\to -\mathrm{\infty }$ta có $f(x_n)\to L$, kí hiệu $\underset{x\to -\mathrm{\infty }}{lim}f(x)=L$ hay $f(x)\to L$ khi $x\to -\mathrm{\infty }$.

* Nhận xét:

- Các quy tắc tính giới hạn hữu hạn tại một điểm cũng đúng cho giới hạn hữu hạn tại vô cực.

- Với c là hằng số, k là một số nguyên dương ta có:

$\underset{x\to +\mathrm{\infty }}{lim}c=c$, $\underset{x\to -\mathrm{\infty }}{lim}c=c$,$\underset{x\to +\mathrm{\infty }}{lim}(\frac{c}{x^k})=0,\underset{x\to -\mathrm{\infty }}{lim}(\frac{c}{x^k})=0$.

III. Giới hạn vô cực (một phía) của hàm số tại một điểm

- Cho hàm số $y=f(x)$xác định trên khoảng $\left(a;+\mathrm{\infty }\right)$. Ta nói hàm số $f(x)$có giới hạn $+\mathrm{\infty }$ khi $x\to a^{+}$ nếu với dãy số $\left(x_n\right)$ bất kì, $x_n>a$ và $x_n\to a$ta có $f(x_n)\to +\mathrm{\infty }$.

Kí hiệu $\underset{x\to a^{+}}{lim}f(x)=+\mathrm{\infty }$hay $f(x)\to +\mathrm{\infty }$ khi $x\to a^{+}$

- Các giới hạn $\underset{x\to a^{+}}{lim}f(x)=-\mathrm{\infty },\underset{x\to a^{-}}{lim}f(x)=+\mathrm{\infty },\underset{x\to a^{-}}{lim}f(x)=-\mathrm{\infty }$ được định nghĩa tương tự.

IV. Giới hạn vô cực của hàm số tại vô cực

- Cho hàm số $y=f(x)$ xác định trên khoảng $\left(a;x_0\right)$. Ta nói hàm số $f(x)$có giới hạn $+\mathrm{\infty }$ khi $x\to x_0$ về bên trái nếu với dãy số $\left(x_n\right)$bất kì, $x_n>a$ và $x_n\to +\mathrm{\infty }$ ta có $f(x_n)\to +\mathrm{\infty }$, kí hiệu $\underset{x\to +\mathrm{\infty }}{lim}f(x)=+\mathrm{\infty }$.

Kí hiệu $\underset{x\to +\mathrm{\infty }}{lim}f(x)=+\mathrm{\infty }$ hay $f(x)\to +\mathrm{\infty }$ khi $x\to +\mathrm{\infty }$.

- Các giới hạn $\underset{x\to +\mathrm{\infty }}{lim}f(x)=-\mathrm{\infty },\underset{x\to -\mathrm{\infty }}{lim}f(x)=+\mathrm{\infty },\underset{x\to -\mathrm{\infty }}{lim}f(x)=-\mathrm{\infty }$ được định nghĩa tương tự.

* Chú ý:

• $\underset{x\to +\mathrm{\infty }}{lim}{x}^k=+\mathrm{\infty },k\in {\mathbb{Z}}^{+}.$
• $\underset{x\to -\mathrm{\infty }}{lim}{x}^k=+\mathrm{\infty },$ k là số nguyên dương chẵn.
• $\underset{x\to -\mathrm{\infty }}{lim}{x}^k=-\mathrm{\infty },$ k là số nguyên dương lẻ.