Lý thuyết Hình lăng trụ và hình hộp (Cánh diều 2024) Toán 11
Tóm tắt lý thuyết Toán 11 Bài 5: Hình lăng trụ và hình hộp ngắn gọn, chính xác sách Cánh diều sẽ giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt Toán 11.
Lý thuyết Toán 11 Bài 5: Hình lăng trụ và hình hộp - Cánh diều
A. Lý thuyết Hình lăng trụ và hình hộp
I. Hình lăng trụ
1. Định nghĩa
- Hình gồm hai đa giác A1A2...An, A1′A2′...An′ và các tứ giác A1A1′A2′A2,A2A2′A3′A3,…,AnAn′A1′A1 được gọi là hình lăng trụ và kí hiệu là A1A2...An.A1′A2′...An′.
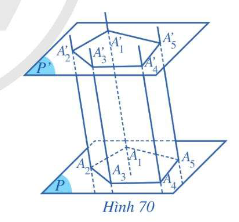
- Trong hình lăng trụ A1A2...An.A1′A2′...An′
+ Các điểm A1,A2,...,An và A1′,A2′,...,An′ được gọi là các đỉnh.
+ Các đoạn thẳng A1A1′,A2A2′,...,AnAn′ được gọi là các cạnh bên, các đoạn thẳng.A1A2,A2A3,...,AnA1và A1′A2′,A2′A3′,...,An′A1′ gọi là cạnh đáy của hình trụ.
+ Hai đa giác A1A2...Anvà A1′A2′...An′ được gọi là hai mặt đáy của hình lăng trụ.
+ Các tứ giác A1A1′A2′A2,A2A2′A3′A3,…,AnAn′A1′A1 gọi là các mặt bên của hình trụ.
* Chú ý: Nếu đáy của lăng trụ là một tam giác, tứ giác, ngũ giác,… thì lăng trụ tương ứng gọi là hình lăng trụ tam giác, hình lăng trụ tứ giác, hình lăng trụ ngũ giác.
2. Tính chất
- Các cạnh bên của hình lăng trụ song song và bằng nhau.
- Các mặt bên của hình lăng trụ là các hình bình hành.
- Hai mặt đáy của hình lăng trụ là hai đa giác có các cạnh tương ứng song song và bằng nhau.
II. Hình hộp
1. Định nghĩa
- Hình hộp là hình lăng trụ có đáy là hình bình hành.
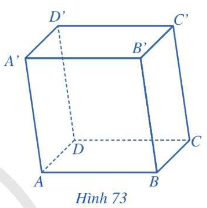
- Trong mỗi hình hộp, ta gọi:
+ Hai mặt không có đỉnh chung là hai mặt đối diện.
+ Hai cạnh song song không nằm trong một mặt phẳng là hai cạnh đối diện.
+ Hai đỉnh không thuộc cùng một mặt là hai đỉnh đối diện.
+ Đoạn thẳng nối hai đỉnh đối diện là đường chéo.
2. Tính chất
- Các mặt của hình hộp là hình bình hành.
- Hai mặt phẳng lần lượt chứa hai mặt đối diện của hình hộp song song với nhau.
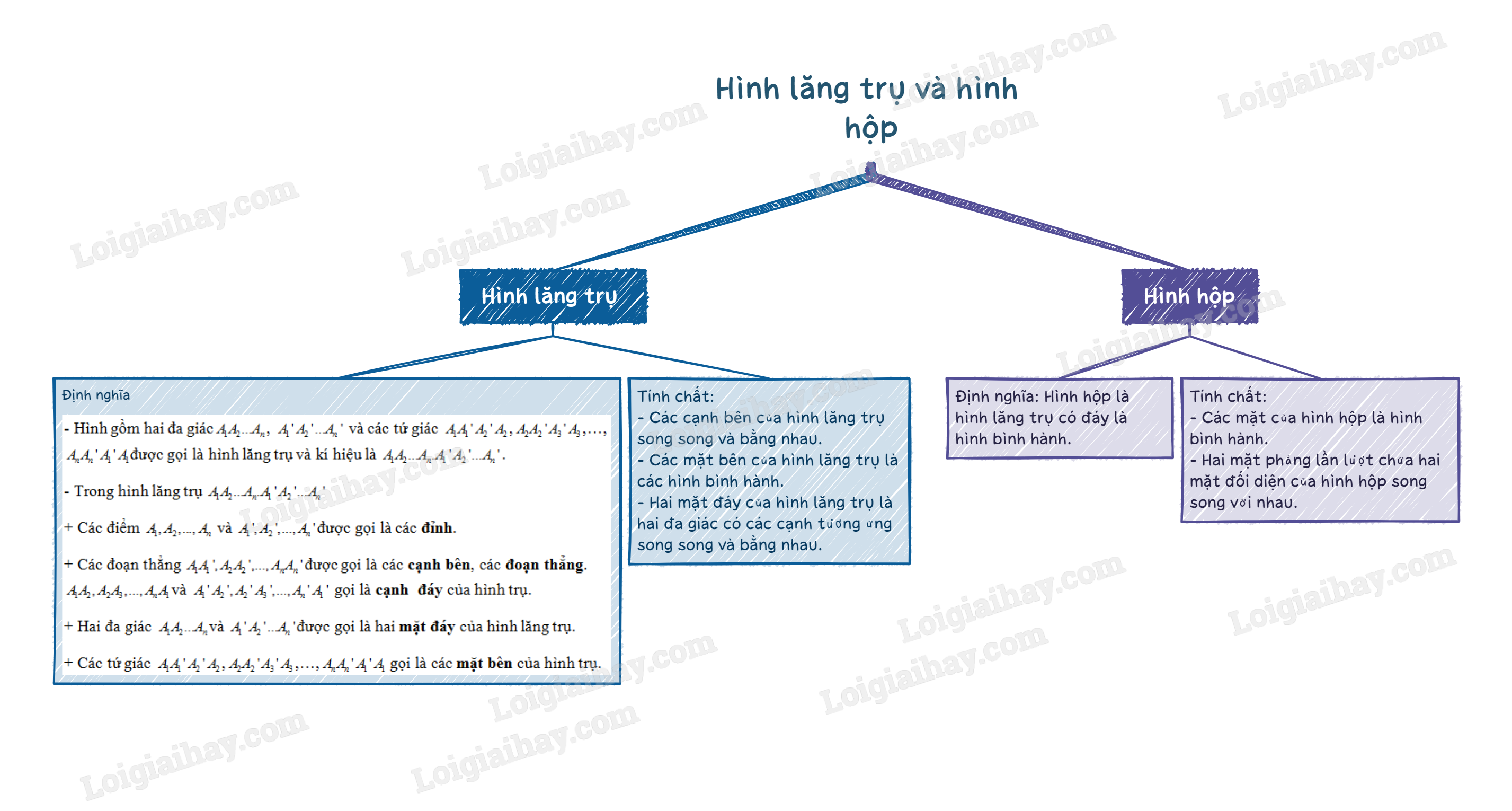
B. Bài tập Hình lăng trụ và hình hộp
Đang cập nhật ...