Lý thuyết Phép tính lôgarit (Cánh diều 2024) Toán 11

Lý thuyết Toán 11 Bài 2: Phép tính lôgarit - Cánh diều

A. Lý thuyết Phép tính lôgarit

1. Khái niệm lôgarit

a) Định nghĩa

Với a > 0, a $\ne$ 1 và b > 0, ta có: $c={\log }_{a}b\iff a^c=b$. Ngoài ra:

- Lôgarit thập phân của b là lôgarit cơ số 10 của số thực dương b:

$c=\log b\iff {10}^c=b$

- Lôgarit tự nhiên của b là lôgarit cơ số e của số thực dương b:

$c=\ln b\iff e^c=b$.

b) Tính chất

Với a > 0, a $\ne$ 1 và b > 0, ta có:

${\log }_{a}1=0$; ${\log }_{a}a=1$; ${\log }_a{a}^c=c$; $a^{{\log }_{a}b}=b$.

2. Một số tính chất của phép tính lôgarit

Trong mục này, ta xét a > 0, a $\ne$ 1 và b > 0.

a) Lôgarit của một tích, một thương

Với m > 0, n > 0, ta có:

• ${\log }_a\left(mn\right)={\log }_{a}m+{\log }_{a}n$;
• ${\log }_a\left(\frac{m}{n}\right)={\log }_{a}m-{\log }_{a}n$.

Nhận xét: ${\log }_a\left(\frac{1}{b}\right)=-{\log }_{a}b$.

b) Lôgarit của một lũy thừa

Với mọi số thực $\alpha$, ta có: ${\log }_a{b}^{\alpha }=\alpha {\log }_{a}b$.

Nhận xét: Với mọi số nguyên dương $n\ge 2$, ta có: ${\log }_a\sqrt[n]{b}=\frac{1}{n}{\log }_{a}b$.

c) Đổi cơ số của lôgarit

Với a, b là hai số thực dương khác 1 và c là số thực dương, ta có: ${\log }_{b}c=\frac{{\log }_{a}c}{{\log }_{a}b}$.

Nhận xét: Với a, b là hai số thực dương khác 1, c > 0 và $\alpha \ne 0$, ta có những công thức sau:

• ${\log }_{a}b.{\log }_{b}c={\log }_{a}c$;
• ${\log }_{a}b=\frac{1}{{\log }_{b}a}$;
• ${\log }_{a^{\alpha }}b=\frac{1}{\alpha }{\log }_{a}b$.

Sơ đồ tư duy Phép tính lôgarit

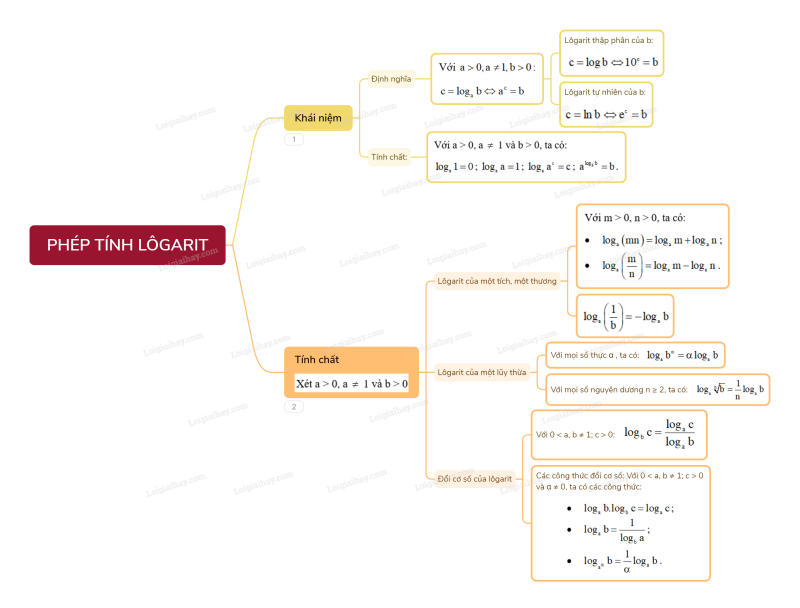
B. Bài tập Phép tính lôgarit

Đang cập nhật ...