Lý thuyết Hai mặt phẳng vuông góc (Cánh diều 2024) Toán 11

Lý thuyết Toán 11 Bài 4: Hai mặt phẳng vuông góc - Cánh diều

A. Lý thuyết Hai mặt phẳng vuông góc

1. Định nghĩa

Hai mặt phẳng cắt nhau tạo nên bốn góc nhị diện. Nếu một trong các góc nhị diện đó là hai góc nhị diện vuông thì hai mặt phẳng đã cho gọi là vuông góc với nhau.

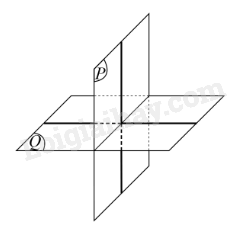
Ví dụ: Hai mặt phẳng (P) và (Q) cắt nhau tạo nên bốn góc nhị diện. Nếu một trong bốn góc nhị diện đó là góc nhị diện vuông thì vta nói (P) vuông góc với (Q), kí hiệu là $\left(P\right)\mathrm{\perp }\left(Q\right)$ hoặc $\left(Q\right)\mathrm{\perp }\left(P\right)$.

2. Điều kiện để hai mặt phẳng vuông góc

Nếu mặt phẳng này chứa một đường thẳng mà đường thẳng đó vuông góc với mặt phẳng kia thì hai mặt phẳng đó vuông góc với nhau.

3. Tính chất

- Tính chất 1: Nếu hai mặt phẳng vuông góc với nhau thì bất cứ đường thẳng nào nằm trong mặt phẳng này và vuông góc với giao tuyến cùng vuông góc với mặt phẳng kia.

- Tính chất 2: Nếu hai mặt phẳng cắt nhau và cùng vuông góc với mặt phẳng thứ ba thì giao tuyến của chúng vuông góc với mặt phẳng thứ ba đó.

Nhận xét:

- Cho hai mặt phẳng (P) và (Q) vuông góc với nhau. Nếu qua một điểm trong mặt phẳng (P) ta dựng đường thẳng vuông góc với mặt phẳng (Q) thì đường thẳng này nằm trong mặt phẳng (P).

- Nếu hai mặt phẳng vuông góc với nhau thì hình chiếu của một đường thẳng nằm trong mặt phẳng này trên mặt phẳng kia đều trùng hoặc nằm trên giao tuyến.

- Ta có thể chứng minh đường thẳng vuông góc với mặt phẳng bằng cách sử dụng Tính chất 1.

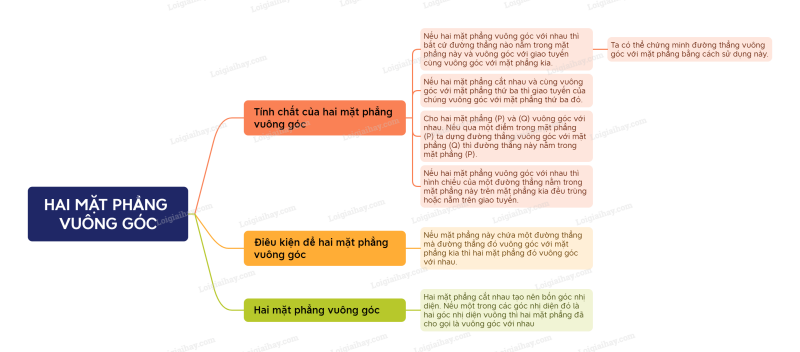
Sơ đồ tư duy Hai mặt phẳng vuông góc

B. Bài tập Hai mặt phẳng vuông góc

Đang cập nhật ...