Chỉ ra phép quay có thể biến mỗi hình trong Hình 10 thành chính nó.

Cho hình chữ nhật ABCD. Gọi E, F, H, K, L, I, J lần lượt là trung điểm của AB, BC, CD, DA, KF, HC, HL. Chứng minh hình thang AEJK và hình thang FLIC bằng nhau.

Cho hai tam giác đều ABC và AB’C’ như Hình 9. Gọi M, N lần lượt là trung điểm của BB’ và CC’. Chứng minh ∆AMN đều.

Trong mặt phẳng tọa độ Oxy, cho các điểm A(–4; 2), B(–4; 5) và C(–1; 3).

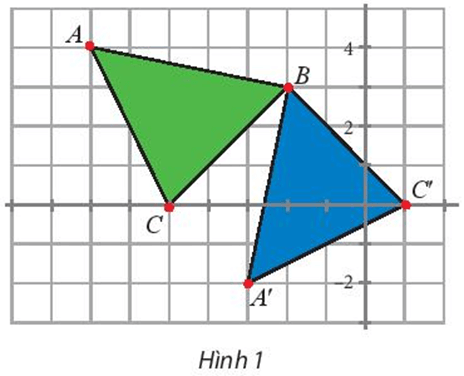
a) Chứng minh các điểm A’(2; 4), B’(5; 4) và C’(3; 1) theo thứ tự là ảnh của A, B, C qua phép quay tâm O với góc quay –90°.

b) Gọi ∆A₁B₁C₁ là ảnh của ∆ABC qua phép dời hình có được bằng cách thực hiện phép quay tâm O với góc quay –90° và phép đối xứng qua Ox. Tìm tọa độ các đỉnh của ∆A₁B₁C₁.

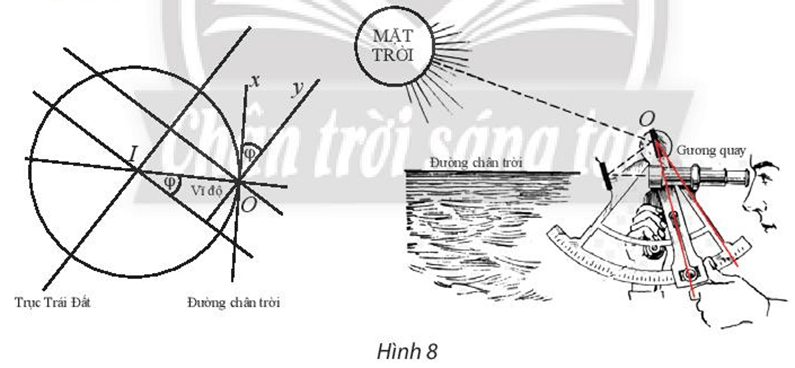
Kính lục phân là một dụng cụ quang học sử dụng gương quay để thực hiện phép quay Q_{(O, φ)} biến tia Ox (song song với đường chân trời) thành tia Oy (song song với trục Trái Đất), nhờ đó đo được góc φ giữa trục của Trái Đất và đường chân trời tại vị trí của người đo. Hãy giải thích tại sao góc φ của phép quay này lại cho ta vĩ độ tại điểm sử dụng kính.

Cho hình vuông ABCD có cạnh bằng a và có tâm I, tìm ảnh qua phép quay Q_{(I, 90°)} của các hình sau:

a) Tam giác IAB;

b) Đường thẳng BC;

c) Đường tròn (B, a).

Cho phép quay Q_{(O; φ)} và hai điểm tùy ý A, B (O, A, B không thẳng hàng) như Hình 6. Vẽ A’, B’ là ảnh của A, B qua phép quay. Hai tam giác OAB và OA’B’ có bằng nhau không?

Một con tàu đang di chuyển theo hướng bắc. Người lái tàu phải thực hiện phép quay nào trên bánh lái để con tàu:

a) rẽ sang hướng tây?

b) rẽ sang hướng đông?

Trong mặt phẳng tọa độ Oxy, tìm tọa độ của các điểm là ảnh của điểm $M\left(\sqrt{2};\sqrt{2}\right)$ lần lượt qua các phép quay Q_{(O, 45°)}, Q_{(O, 90°)}, Q_{(O, 180°)}, Q_{(O, 360°)}.

a) Tìm phép biến hình biến ∆BAC thành ∆BA’C’ (Hình 1).

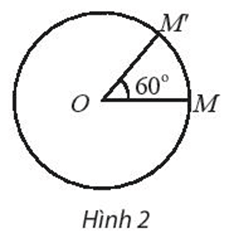
b) Trong mặt phẳng, cho điểm O cố định (Hình 2).

Gọi f là quy tắc ứng với mỗi điểm M trùng O cho ta điểm O và ứng với điểm M khác O cho ta một điểm M’ xác định như sau:

– Dùng compa vẽ đường tròn (C) tâm O bán kính OM.

– Trên (C) chọn điểm M’ sao cho góc lượng giác (OM, OM’) bằng 60°.

Quy tắc f có phải là một phép biến hình không?

Hãy vẽ điểm M’ theo quy tắc trên nếu thay góc 60° bởi góc –30°.

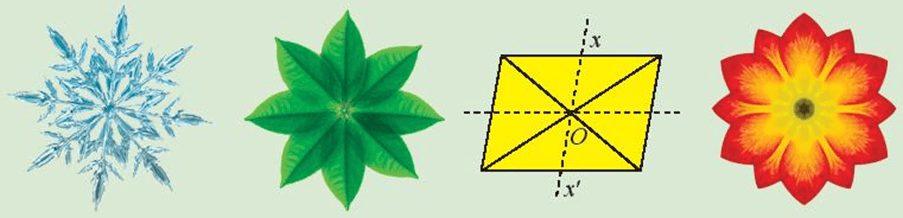
Vẽ mỗi hình sau ra một tờ giấy, cắt rời mỗi hình theo hình tròn. Tìm một điểm O trên mỗi hình. Sau đó, ghim hình đã cắt được xuống mặt bàn tại điểm O, thử xoay hình một góc φ nào đó. Có nhận xét gì về kích thước của hình trước khi xoay và sau khi xoay?

Vận dụng phép đối xứng tâm và đối xứng trục để cắt hoa văn trang trí theo hướng dẫn sau:

– Lấy một tờ giấy hình vuông, gấp đôi, gấp tư rồi gấp làm tám (Hình 14a).

– Vẽ hoa và lá trên bề mặt tam giác (Hình 14b).

– Dùng kéo cắt theo đường đã vẽ (Hình 14c).

– Trải phẳng tờ giấy ra để thấy hoa văn trang trí gồm hoa và lá (Hình 14d).

Tìm tâm đối xứng và trục đối xứng của hoa văn vừa làm.

Nghệ thuật cắt giấy Kirigami của Nhật Bản đã sử dụng rất nhiều phép đối xứng khi cắt để tạo ra các hình đẹp. Hãy tìm trục đối xứng và tâm đối xứng của các hình trong Hình 13.

Trong Hình 12, tìm phép đối xứng biến hình mũi tên (A) thành hình mũi tên (B) và tìm phép đối xứng biến hình mũi tên (B) thành hình mũi tên (C).

Trong Hình 11, hình nào có trục đối xứng, hình nào có tâm đối xứng?

Cho hình bình hành ABCD có AC cố định còn B di động trên (O; R). Hãy cho biết D di động trên đường nào.

Cho đường tròn (O; R) và điểm I không nằm trên đường tròn. Với mỗi điểm A trên (O; R) ta xét hình vuông ABCD có tâm là I. Điểm C di động trên đường nào khi A di động trên đường tròn (O; R)?

Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) có phương trình:

(C): x² + y² – 4x – 5 = 0. Viết phương trình ảnh của (C) qua phép đối xứng tâm O.

Trong Hình 10, hình nào có tâm đối xứng? (Mỗi chữ cái là một hình).

a) Trong Hình 9, hình nào có tâm đối xứng? Tìm tâm đối xứng (nếu có).

b) Nêu tên một hình có vô số tâm đối xứng.

Tìm phép đối xứng trục và phép đối xứng tâm biến Hình 7 thành chính nó.

Trong Hình 6, tìm các số ghi tại điểm đối xứng qua tâm bia với điểm ghi các số 20; 7; 9.

Trong mặt phẳng tọa độ Oxy, tìm ảnh qua Đ_O của

a) điểm M(3; –4);

b) đường thẳng d: x – 3y + 6 = 0;

c) đường tròn (C): (x + 2)² + (y – 1)² = 4.

Giả sử Đ_O là phép đối xứng tâm O. Lấy hai điểm tùy ý A, B sao cho ba điểm O, A, B không thẳng hàng. Gọi A’, B’ lần lượt là ảnh của A, B qua Đ_O. So sánh tam giác OAB và tam giác O’A’B’ rồi so sánh A’B’ và AB.

Tìm phép đối xứng tâm biến mỗi hình sau thành chính nó. 

Trong mặt phẳng tọa độ Oxy, cho các điểm I(1; 1), M(2; 2), N(0; –3) và P(–1; –2). Tìm tọa độ các điểm M’ = Đ_I(M), N’ = Đ_I(N), P’ = Đ_I(P).

Cho điểm O. Gọi f là quy tắc xác định như sau:

a) Với điểm M khác O, xác định điểm M’ sao cho O là trung điểm của MM’ (Hình 1).

b) Với điểm M trùng với O thì f biến điểm M thành chính nó.

Hỏi f có phải là phép biến hình không?

Trong các hình sau, hình nào có tâm đối xứng?

Tồn tại hay không phép biến hình biến mỗi hình phẳng sau đây thành chính nó?

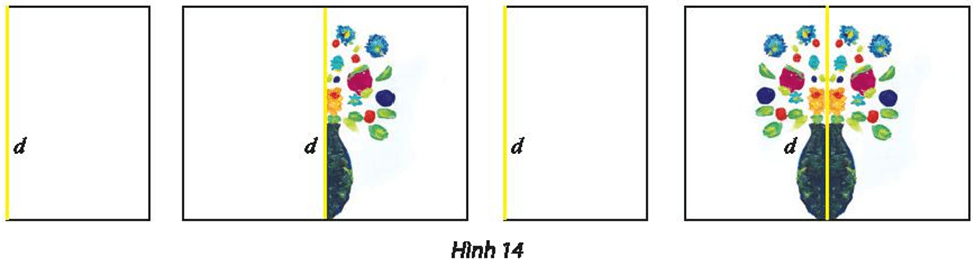
Vận dụng phép đối xứng trục để vẽ nhanh bình hoa theo hướng dẫn trong Hình 14.

– Gấp đôi một tờ giấy trắng A4 theo nếp gấp d.

– Mở tờ giấy ra, ở một phía của nếp gấp d, nhỏ vài giọt màu nước có màu khác nhau làm hoa và một giọt màu đen làm bình hoa.

– Gấp lại tờ giấy theo nếp gấp d, chà nhẹ để màu thấm đều sang hai bên.

– Mở tờ giấy ra, ta có một bình hoa đẹp.

Tìm trục đối xứng của hình vừa vẽ.

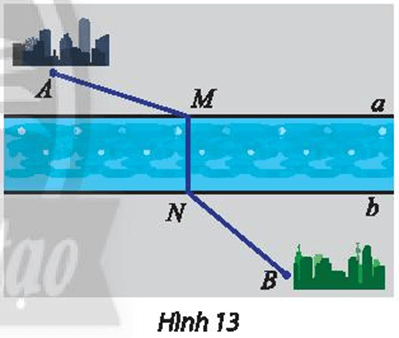
Hai thành phố A, B nằm ở hai bên bờ của một con sông (Hình 13). Giả sử hai bờ sông là hai đường thẳng song song a, b. Tìm vị trí điểm M bên bờ a và N bên bờ b để xây dựng một chiếc cầu MN sao cho MN vuông góc với a, b và tổng khoảng cách AM + NB ngắn nhất.

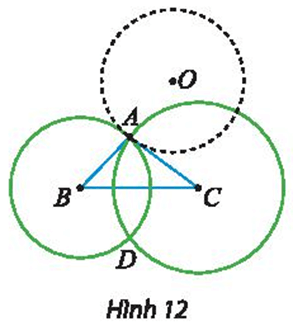
Cho tam giác ABC với B và C cố định. Vẽ hai đường tròn có tâm lần lượt là B, C và đi qua A. Gọi D là giao điểm thứ hai của hai đường tròn nói trên (Hình 12). Khi A di động trên một đường tròn cố định (O) thì điểm D di động trên đường nào?

Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): (x – 3)² + (y – 4)² = 25 và đường thẳng ∆: 2x + 3y + 4 = 0.

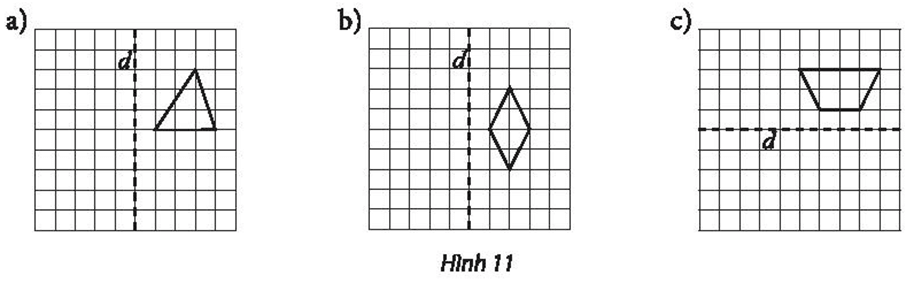
a) Tìm ảnh của (C) và ∆ qua phép đối xứng trục Ox.

b) Tìm ảnh của (C) và ∆ qua phép đối xứng trục Oy.

c) Tìm ảnh của (C) và ∆ qua phép đối xứng trục d: x – y – 3 = 0.

Trong mặt phẳng tọa độ Oxy, cho ba điểm A(3; 2), B(4; –3) và M(–8; 5).

a) Tìm ảnh của A qua Đ_Ox và ảnh của B qua Đ_Oy.

b) Biết M là ảnh của N qua Đ_Oy. Xác định tọa độ của N.

Trong mặt phẳng tọa độ Oxy, cho đường thẳng d có phương trình x – y = 0 và cho điểm M(x₀; y₀). Tìm tọa độ điểm M’ = Đ_d(M).

Vẽ các hình sau đây vào giấy kẻ ô vuông và tìm ảnh của các hình đã cho qua phép đối xứng trục d.

Tìm trục đối xứng trong các hình ở Hình 10.

Tìm trục đối xứng của một hình thang cân ABCD có hai đáy là AB và CD.

Cho tam giác ABC cân tại A và M là trung điểm của BC. Tìm ảnh của tam giác ABC qua phép đối xứng trục AM.

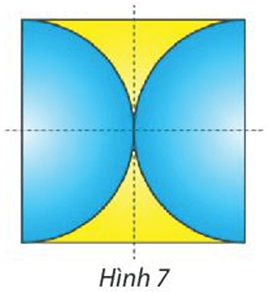
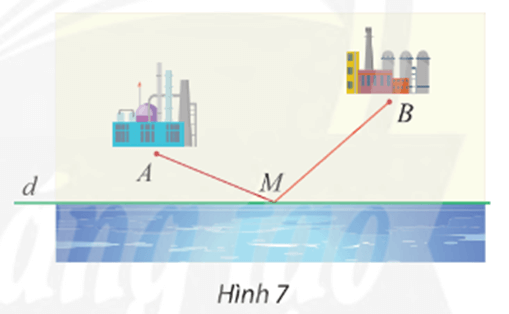
Cho hai điểm A, B là vị trí của hai nhà máy nằm cùng một phía bờ sông là đường thẳng d. Tìm trên bờ sông một địa điểm M để xây dựng một trạm bơm sao cho tổng chiều dài đường ống dẫn nước từ trạm bơm về hai nhà máy là ngắn nhất (Hình 7).

Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: x – y + 3 = 0 và đường tròn (C): (x + 1)² + (y + 2)² = 9.

a) Tìm ảnh của đường thẳng d qua Đ_Oy.

b) Tìm ảnh của đường tròn (C) qua Đ_Ox.