Câu hỏi:
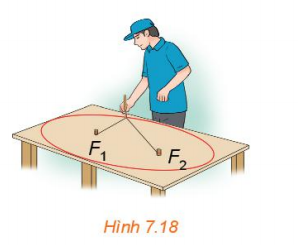
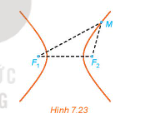
89 lượt xemHoạt động 3 trang 50 Toán 10 Tập 2: Giả sử thiết bị tại F2 nhận được tín hiệu âm thanh sớm hơn thiết bị tại F1 là 2 giây và vận tốc âm thanh là 343 m/s.
a) Tìm mối quan hệ giữa các khoảng cách từ nơi phát ra tín hiệu âm thanh tới F1, F2.
b) Việc giới hạn khu vực tìm kiếm nơi phát ra tín hiệu âm thanh có liên quan đến bài toán tìm tập hợp những điểm M thỏa mãn MF1 – MF2 = 686 (m) hay không?
Lời giải
Hướng dẫn giải:
Lời giải
a) Gọi M là điểm phát tín hiệu âm thanh, t (s) là thời gian âm thanh truyền từ M đến F2.
Khi đó âm thanh truyền từ M đến F1 là: t + 2 (s)
Khoảng cách từ M đến F1 là: MF1 = 343(t + 2) = 343t + 686 (m).
Khoảng cách từ M đến F2 là: MF2 = 343.t = 343t (m).
Suy ra MF1 – MF2 = 343t + 686 – 343t = 686 (m).
Vậy hiệu khoảng cách từ nơi phát tín hiệu tới F1 và tới F2 luôn không đổi và bằng 686m.
b) Ta thấy nơi phát tín hiệu luôn thỏa mãn hiệu khoảng cách từ nơi phát tín hiệu tới F1 và tới F2 luôn không đổi và bằng 686m. Do đó đây chính là bài toán tìm điểm M thỏa mãn MF1 – MF2 = 686 (m).
Câu hỏi trang 50 Toán 10 Tập 2: Tại sao trong định nghĩa hypebol cần điều kiện a < c?
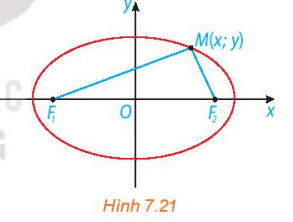
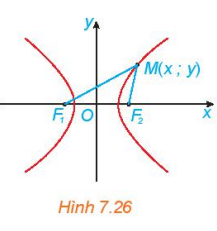
Hoạt động 4 trang 51 Toán 10 Tập 2: Xét một hypebol (H) với các kí hiệu như trong định nghĩa. Chọn hệ trục toạ độ Oxy có gốc O là trung điểm F1F2, tia Ox trùng tia OF2 (H.7.26). Nêu toạ độ của các tiêu điểm F1; F2. Giải thích vì sao điểm M(x; y) thuộc (H) khi và chỉ khi
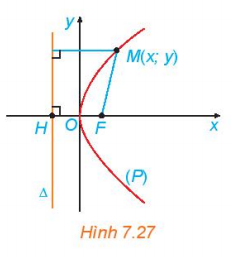
Hoạt động 5 trang 52 Toán 10 Tập 2: Xét (P) là một parabol với tiêu điểm F và đường chuẩn ∆. Gọi p là tham số tiêu của (P) và H là hình chiếu vuông góc của F trên ∆. Chọn hệ trục toạ độ Oxy có gốc O là trung điểm của HF, tia Ox trùng tia OF( H.7.27)
a) Nêu toạ độ của F và phương trình của ∆
b) Giải thích vì sao điểm M(x; y) thuộc (P) khi và chỉ khi
