Câu hỏi:
151 lượt xemGiải Toán 10 trang 53 Tập 2
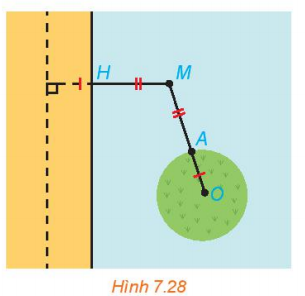
Vận dụng 2 trang 53 Toán 10 Tập 2: Tại một vùng biển giữa đất liền và một đảo, người ta phân định một đường ranh giới cách đều đất liền và đảo (H.7.28). Coi bờ biển vùng đất liền đó là một đường thẳng và đảo là hình tròn. Hỏi đường ranh giới nói trên có hình gì? Vì sao?
Lời giải
Hướng dẫn giải:
Lời giải
Gọi d là đường bờ biển, kẻ một đường thẳng ∆ nằm trong đất liền song song với d sao cho khoảng cách giữa hai đường thẳng OA.
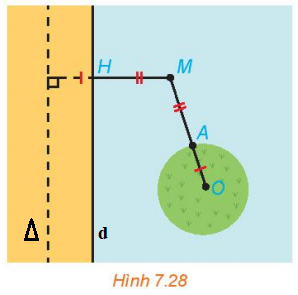
Khi đó ta có:
d(M; ∆) = MH + OA
Mà MH = MA nên d(M; ∆) = MH + OA = MA + OA = MO
Ta có khoảng cách từ điểm M bất kì thuộc đường ranh giới đến đường thẳng ∆ bằng với khoảng cách từ điểm M đến điểm O là tâm của hòn đảo.
Nếu ta coi ∆ là đường chuẩn, điểm O của hòn đảo là vị trí tiêu điểm F thì điểm M cách đều đường chuẩn ∆ và tiêu điểm F nên M nằm trên đường parabol.
Vậy đường ranh giới là tập hợp các điểm cách đều đất liền và đảo hay chính là đường parabol.
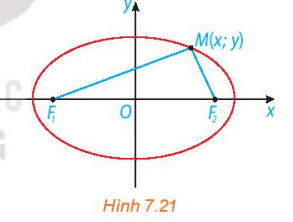
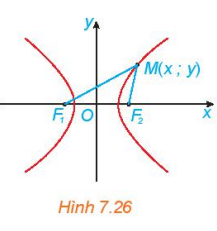
Hoạt động 4 trang 51 Toán 10 Tập 2: Xét một hypebol (H) với các kí hiệu như trong định nghĩa. Chọn hệ trục toạ độ Oxy có gốc O là trung điểm F1F2, tia Ox trùng tia OF2 (H.7.26). Nêu toạ độ của các tiêu điểm F1; F2. Giải thích vì sao điểm M(x; y) thuộc (H) khi và chỉ khi
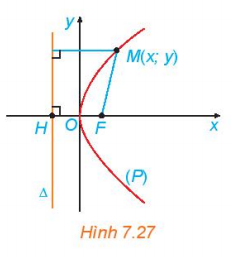
Hoạt động 5 trang 52 Toán 10 Tập 2: Xét (P) là một parabol với tiêu điểm F và đường chuẩn ∆. Gọi p là tham số tiêu của (P) và H là hình chiếu vuông góc của F trên ∆. Chọn hệ trục toạ độ Oxy có gốc O là trung điểm của HF, tia Ox trùng tia OF( H.7.27)
a) Nêu toạ độ của F và phương trình của ∆
b) Giải thích vì sao điểm M(x; y) thuộc (P) khi và chỉ khi