30 câu Trắc nghiệm Các trường hợp bằng nhau của tam giác vuông (có đáp án 2024) – Toán 7 Kết nối tri thức
Bộ 30 câu hỏi trắc nghiệm Toán 7 (có đáp án) Bài 4: Các trường hợp bằng nhau của tam giác vuông đầy đủ các mức độ sách Kết nối tri thức giúp học sinh ôn luyện trắc nghiệm Toán 7 Bài 4.
Trắc nghiệm Toán 7 Bài 15: Các trường hợp bằng nhau của tam giác vuông
I. Nhận biết
Câu 1. Cho ∆ABC vuông tại B và ∆DEF vuông tại E có AB = DE và BC = EF. Khi đó ∆ABC = ∆DEF theo trường hợp:
A. cạnh huyền – cạnh góc vuông;
B. cạnh huyền – góc nhọn;
C. cạnh – góc – cạnh;
D. góc – cạnh – góc.
Hướng dẫn giải
Đáp án: C
Giải thích:
Xét ∆ABC và ∆DEF, có:
^ABC=^DEF=90°.
AB = DE (giả thiết)
BC = EF (giả thiết)
Do đó ∆ABC = ∆DEF (c.g.c)
Vậy ta chọn phương án C.
Câu 2. Cho ∆ABC và ∆PQR. Giả thiết nào dưới đây không suy ra được ∆ABC = ∆PQR?
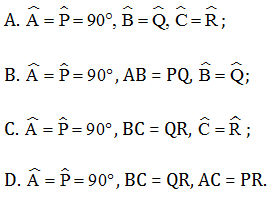
Hướng dẫn giải
Đáp án: A
Giải thích:
⦁ Xét phương án A:
Xét ∆ABC và ∆PQR, có:

⦁ Xét phương án C:
Xét ∆ABC và ∆PQR, có:
.
BC = QR (giả thiết)
(giả thiết)
Do đó ∆ABC = ∆PQR (cạnh huyền – góc nhọn)
⦁ Xét phương án D:
Xét ∆ABC và ∆PQR, có:
.
BC = QR (giả thiết)
AC = PR (giả thiết)
Do đó ∆ABC = ∆PQR (cạnh huyền – cạnh góc vuông)
Vậy ta chọn phương án A.
Câu 3. Phát biểu nào dưới đây đúng nhất?
A. Nếu hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau;
B. Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau;
C. Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau;
D. Cả A, B, C đều đúng.
Hướng dẫn giải
Đáp án: D
Giải thích:
Phương án A: Phát biểu của trường hợp cạnh góc vuông – góc nhọn kề (hay g.c.g).
Phương án B: Phát biểu của trường hợp cạnh huyền – cạnh góc vuông.
Phương án C: Phát biểu của trường hợp cạnh huyền – góc nhọn.
Vậy ta chọn phương án D.
Câu 4. Trong các phương án sau, phương án nào chứa hình có hai tam giác vuông không bằng nhau?
A. 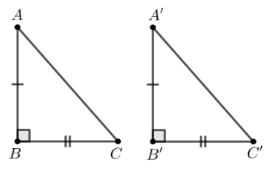
B. 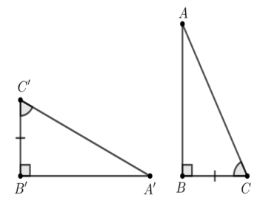
C. 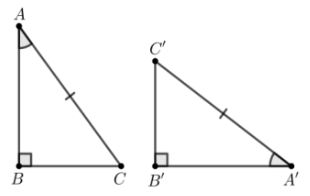
D. 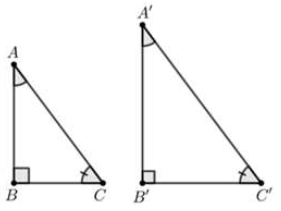
Hướng dẫn giải
Đáp án: D
Giải thích:
⦁ Xét phương án A:
Xét ∆ABC và ∆A’B’C’, có:
.
AB = A’B’ (giả thiết)
BC = B’C’ (giả thiết)
Do đó ∆ABC = ∆A’B’C’ (c.g.c)
Vì vậy phương án A có chứa hai tam giác vuông bằng nhau.
⦁ Xét phương án B:
Xét ∆A’B’C’ và ∆ABC, có:
.
B’C’ = BC (giả thiết)
(giả thiết)
Do đó ∆A’B’C’ = ∆ABC (g.c.g)
Vì vậy phương án B có chứa hai tam giác vuông bằng nhau.
⦁ Xét phương án C:
Xét ∆ABC và ∆A’B’C’, có:
.
AC = A’C’ (giả thiết)
(giả thiết)
Do đó ∆ABC = ∆A’B’C’ (cạnh huyền – góc nhọn)
Vì vậy phương án C có chứa hai tam giác vuông bằng nhau.
⦁ Xét phương án D:
Xét ∆ABC và ∆A’B’C’, có:
.
(giả thiết)
(giả thiết)
Do đó ∆ABC và ∆A’B’C’ không bằng nhau do không có trường hợp bằng nhau góc – góc – góc.
Vậy ta chọn phương án D.
Câu 5. Cho ∆MNP vuông tại P và ∆XYZ vuông tại Z có MP = XZ. Để ∆MNP = ∆XYZ theo trường hợp cạnh huyền – cạnh góc vuông thì cần thêm điều kiện gì?
A. MN = XY;
B. MN = YZ;
C. ;
D. .
Hướng dẫn giải
Đáp án: A
Giải thích:
Ta thấy MP, XZ lần lượt là cạnh góc vuông của ∆MNP và ∆XYZ.
Do đó để ∆MNP = ∆XYZ theo trường hợp cạnh huyền – cạnh góc vuông thì cần thêm điều kiện hai cạnh huyền của hai tam giác đó bằng nhau. Nghĩa là, MN = XY.
Vậy ta chọn phương án A.
II. Thông hiểu
Câu 1. Cho ∆ABC có AB = AC và . Trên cạnh BC, lấy hai điểm D và E sao cho BD = EC. Kẻ DM vuông góc với AB (M ∈ AB) và EN vuông góc với AC (N ∈ AC). Kết luận nào sau đây đúng nhất?
A. ∆AMD = ∆ANE;
B. ∆ABD = ∆ACE;
C. MD = EN;
D. Cả A, B, C đều đúng.
Hướng dẫn giải
Đáp án: D
Giải thích:
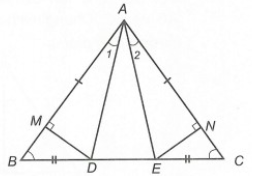
Xét ∆ABD và ∆ACE, có:
BD = EC (giả thiết)
(giả thiết)
AB = AC (giả thiết)
Do đó ∆ABD = ∆ACE (c.g.c)
Suy ra và AD = AE (cặp góc và cặp cạnh tương ứng)
Vì vậy phương án B đúng.
Xét ∆AMD và ∆ANE, có:
.
AD = AE (chứng minh trên)
(chứng minh trên)
Do đó ∆AMD = ∆ANE (cạnh huyền – góc nhọn)
Suy ra MD = EN (cặp cạnh tương ứng)
Vì vậy phương án A, C đúng.
Vậy ta chọn phương án D.
Câu 2. Cho đoạn thẳng BC và điểm H nằm giữa B và C. Qua H kẻ đường thẳng vuông góc với BC. Trên đường thẳng đó lấy các điểm A và K sao cho HA = HK. Kẻ các đoạn thẳng AB, BK, KC, CA. Kết luận nào sau đây sai?
A. BA = BK;
B. ;
C. ;
D. ∆AHB = ∆KHB.
Hướng dẫn giải
Đáp án: B
Giải thích:
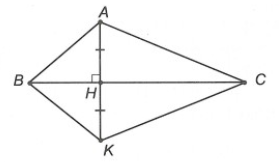
Xét ∆AHB và ∆KHB, có:
HA = HK (giả thiết)
.
BH là cạnh chung.
Do đó ∆AHB = ∆KHB (c.g.c)
Suy ra BA = BK, và (các cặp cạnh và cặp góc tương ứng)
Vì vậy phương án A, C, D đúng, phương án B sai.
Vậy ta chọn phương án B.
Câu 3. Cho ∆ABC có AB = AC. Gọi AM là tia phân giác của ![]() (M ∈ BC). Kẻ MD vuông góc AB (D ∈ AB) và ME vuông góc với AC (E ∈ AC).
(M ∈ BC). Kẻ MD vuông góc AB (D ∈ AB) và ME vuông góc với AC (E ∈ AC).
Cho các khẳng định sau:
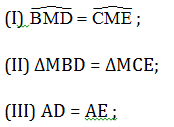
Gọi m là số kết luận đúng và n là số kết luận sai. Giá trị của m và n là:
A. m = 0 và n = 1;
B. m = 2 và n = 1;
C. m = 3 và n = 0;
D. m = 1 và n = 2.
Hướng dẫn giải
Đáp án: C
Giải thích:
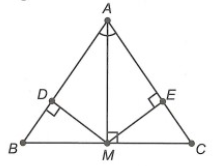
Xét ∆AMD và ∆AME, có:
AM là cạnh chung.
.
(AM là phân giác của )
Do đó ∆AMD = ∆AME (cạnh huyền – góc nhọn)
Suy ra AD = AE và MD = ME (các cặp cạnh tương ứng)
Do đó (III) đúng.
Ta có AB = AC (giả thiết) và AD = AE (chứng minh trên)
Suy ra AB – AD = AC – AE.
Khi đó DB = EC.
Xét ∆MBD và ∆MCE, có:
.
DB = EC (chứng minh trên)
MD = ME (chứng minh trên)
Do đó ∆MBD = ∆MCE (c.g.c). Do đó (II) đúng.
Suy ra (cặp góc tương ứng). Do đó (I) đúng.
Vậy ta có 3 phát biểu đúng và 0 phát biểu sai hay m = 3 và n = 0.
Vậy ta chọn phương án C.
Câu 4. Cho ∆ABC có AB = AC (). Kẻ BD vuông góc với AC (D ∈ AC) và CE vuông góc với AB (E ∈ AB). Gọi H là giao điểm của BD và CE.
Cho bảng sau:
|
A |
B |
|
a. ∆AEC |
1. ∆HDC |
|
b. ∆HEB |
2. ∆CDB |
|
c. ∆BEC |
3. ∆ADB |
Ghép các ý ở cột A với cột B để được một đẳng thức đúng?
A. a – 2; b – 1; c – 3;
B. a – 1; b – 3; c – 2;
C. a – 3; b – 1; c – 2;
D. a – 2; c – 1; b – 3.
Hướng dẫn giải
Đáp án: C
Giải thích:
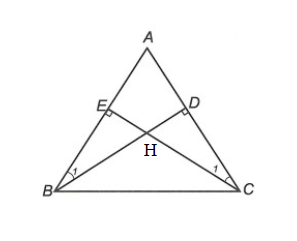
+) Xét ∆ADB và ∆AEC, có:
AB = AC (giả thiết)
.
là góc chung.
Do đó ∆ADB = ∆AEC (cạnh huyền – góc nhọn)
Khi đó a – 3.
+) Vì ∆ADB = ∆AEC nên (cặp góc tương ứng) và AD = BE (cặp cạnh tương ứng)
Ta có: AD + DC = AC, AE + EB = AB
Mà AB = AC, AD = BE nên DC = EB.
Xét ∆HEB và ∆HDC, có:
BE = DC
Suy ra ∆HEB = ∆HDC (g – c – g)
Do đó b – 1.
+) Xét ∆BEC và ∆CDB, có:
BE = DC
BC là cạnh chung
Suy ra ∆BEC = ∆CDB (cạnh góc vuông – cạnh huyền)
Do đó c – 2.
Vậy a – 3, b – 1, c – 2.
Chọn đáp án C.
Câu 5. Cho hình chữ nhật ABCD, M là trung điểm của cạnh BC. Kết luận nào sau đây sai?
A. AM = DM;
B. ∆ABM = ∆ADM ;
C. ;
D. A, B, C sai.
Hướng dẫn giải
Đáp án: D
Giải thích:
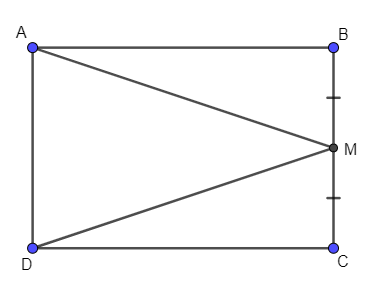
Xét ∆ABM và ∆DCM, có:
AB = DC (ABCD là hình chữ nhật)
(ABCD là hình chữ nhật)
MB = MC (giả thiết)
Do đó ∆ABM = ∆DCM (c.g.c)
Suy ra AM = DM và (cặp cạnh và cặp góc tương ứng)
Ta có: (các cặp góc phụ nhau)
Suy ra
Vì vậy phương án A, B, C đều đúng.
Vậy ta chọn phương án D.
Câu 6. Cho tam giác ABC có AD vuông góc với BC. Biết AB = AC = 3cm, . Tính cạnh BC.
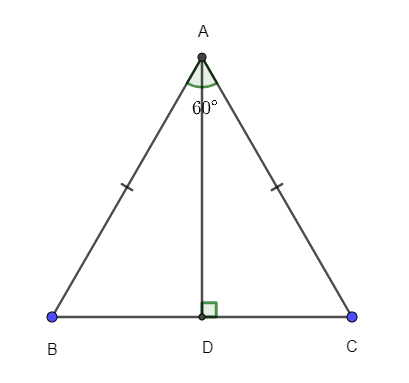
A. BC = 6 cm;
B. BC = 1,5 cm;
C. BC = 9 cm;
D. BC = 3cm.
Hướng dẫn giải
Đáp án: D
Giải thích:
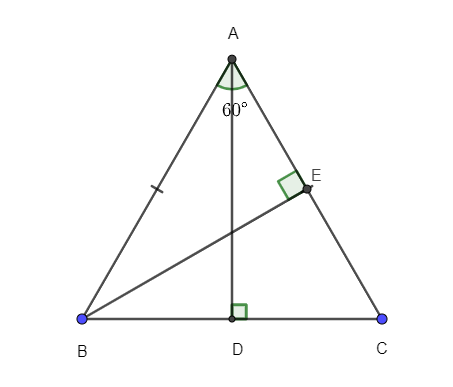
Xét ∆ADB và ∆ADC, có:
AD là cạnh chung.
.
DB = DC (giả thiết)
Do đó ∆ADB = ∆ADC (c.g.c)
(cặp góc tương ứng)
Xét tam giác ABC, có: (định lí tổng ba góc trong tam giác)
.
Kẻ BE vuông góc với AC.
Xét ∆BEA và ∆BEC, có:
BE là cạnh chung
Do đó ∆BEA = ∆BEC (cạnh góc vuông – góc nhọn)
Suy ra AB = BC
Mà AB = 3cm nên BC = 3cm.
Vậy chọn đáp án D.
Câu 7. Cho hình vẽ bên.
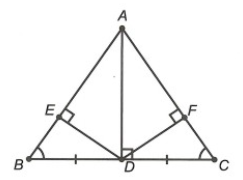
Khẳng định nào sau đây sai?
A. ∆AED = ∆AFD;
B. ∆BED = ∆CFD;
C. ∆ADB = ∆ADC;
D. ∆ADE = ∆AFD.
Hướng dẫn giải
Đáp án: D
Giải thích:
⦁ Xét phương án B:
Xét ∆BED và ∆CFD, có:
.
BD = CD (giả thiết)
(giả thiết)
Do đó ∆BED = ∆CFD (cạnh huyền – góc nhọn)
Vì vậy phương án B đúng.
⦁ Xét ∆AED và ∆AFD, có:
AD là cạnh chung.
ED = FD (∆BED = ∆CFD)
.
Do đó ∆AED = ∆AFD (cạnh huyền – cạnh góc vuông)
Vì vậy phương án A đúng, phương án D sai (do viết sai thứ tự các đỉnh).
⦁ Xét phương án C:
Xét ∆ADB và ∆ADC, có:
AD là cạnh chung.
.
DB = DC (giả thiết)
Do đó ∆ADB = ∆ADC (c.g.c)
Vì vậy phương án C đúng.
Vậy ta chọn phương án D.
III. Vận dụng
Câu 1. Cho ∆ABC có AB = AC (). Vẽ BH ⊥ AC (H ∈ AC), CK ⊥ AB (K ∈ AB). Gọi I là giao điểm của BH và CK. Gọi D là giao điểm của AI và BC. Ta có các phát biểu sau:
(I) AI là tia phân giác của ;
(II) AD ⊥ BC;
(III) D là trung điểm của BC.
Phát biểu đúng là:
A. I và II;
B. II và III;
C. I và III;
D. I, II và III.
Hướng dẫn giải
Đáp án: C
Giải thích:
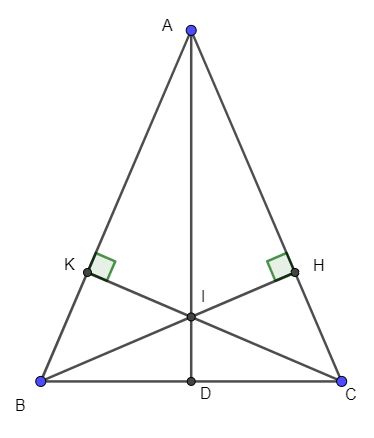
Xét ∆AHB và ∆AKC, có:
.
AB = AC (giả thiết)
là góc chung.
Do đó ∆AHB = ∆AKC (cạnh huyền – góc nhọn)
Suy ra AH = AK (cặp cạnh tương ứng)
Xét ∆AKI và ∆AHI, có:
AI là cạnh chung.
AK = AH (chứng minh trên)
.
Do đó ∆AKI = ∆AHI (cạnh huyền – cạnh góc vuông)
Suy ra (cặp góc tương ứng)
Khi đó AI là tia phân giác của . Do đó (I) đúng.
Xét ∆ABD và ∆ACD, có:
AD là cạnh chung
(chứng minh trên)
AB = AC (chứng minh trên)
Do đó ∆ABD = ∆ACD (c – g – c)
Suy ra BD = CD và (cặp cạnh và cặp góc tương ứng)
Khi đó D là trung điểm của BC. Do đó (III) đúng.
Mặt khác ta có = 180°
Do đó = 90° hay AD ⊥ BC. Suy ra (II) đúng.
Vậy (I), (II) và (III) đều đúng.
Câu 2. Cho ∆ABC vuông tại A có AB < AC. Kẻ AH vuông góc với BC (H ∈ BC). Gọi D là điểm trên cạnh AC sao cho AD = AB. Vẽ DE vuông góc với BC (E ∈ BC) và DK vuông góc với AH (K ∈ AH). Độ dài của HE bằng:
A. HA;
B. KD;
C. Cả A và B đều đúng;
D. Cả A và B đều sai.
Hướng dẫn giải
Đáp án: C
Giải thích:
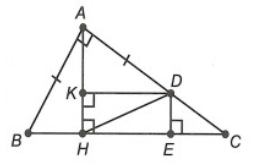
Xét ∆HAB và ∆KDA, có:
AB = AD (giả thiết)
.
(cùng phụ với ).
Do đó ∆HAB = ∆KDA (cạnh huyền – góc nhọn)
Suy ra HA = KD (cặp cạnh tương ứng)
Vì vậy phương án B, D đúng.
Ta có KD ⊥ AH (giả thiết) và EH ⊥ AH (giả thiết)
Suy ra KD // EH.
Suy ra (cặp góc so le trong).
Xét ∆KDH và ∆EHD, có:
.
DH là cạnh chung.
(chứng minh trên)
Do đó ∆KDH = ∆EHD (cạnh huyền – góc nhọn)
Suy ra KD = HE (cặp cạnh tương ứng)
Mà HA = KD (chứng minh trên)
Do đó HA = HE.
Vì vậy phương án C đúng.
Câu 3. Cho đoạn thẳng AB, điểm O nằm giữa A và B. Kẻ tia Ox vuông góc với AB. Trên tia Ox lấy các điểm C và D sao cho OC = OA, OD = OB. Gọi M, N lần lượt là trung điểm của AD và BC. Góc MON là:
A. góc nhọn;
B. góc vuông;
C. góc tù;
D. góc bẹt.
Hướng dẫn giải
Đáp án: B
Giải thích:
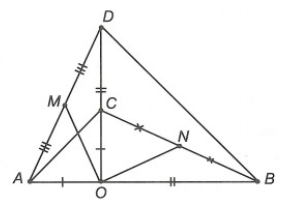
Xét ∆AOD và ∆COB, có:
AO = CO (giả thiết)
OD = OB (giả thiết)
.
Do đó ∆AOD = ∆COB (c.g.c)
Suy ra AD = BC và (cặp cạnh và cặp góc tương ứng)
Ta có M, N lần lượt là trung điểm của AD, BC.
Suy ra và .
Mà AD = BC (chứng minh trên)
Suy ra MD = NB.
Xét ∆OBN và ∆ODM, có:
OB = OD (giả thiết)
BN = MD (chứng minh trên)
(chứng minh trên)
Do đó ∆OBN = ∆ODM (c.g.c)
Suy ra (cặp góc tương ứng)
Ta lại có: (OC ⊥ OB)
Suy ra hay .
Vậy góc MON là góc vuông.